河南省商丘市柘城县实验中学2022-2023学年九年级下学期4月月考数学试题

这是一份河南省商丘市柘城县实验中学2022-2023学年九年级下学期4月月考数学试题，共16页。试卷主要包含了下列计算正确的是等内容，欢迎下载使用。
柘城县实验中学2022-2023学年九年级下学期第二次月考
数学
注意事项：
1．本试卷共6页，三个大题，满分120分，考试时间100分钟。
2．本试卷上不要答题，请按答题卡上注意事项的要求直接把答案填写在答题卡上。答在试卷上的答案无效。
一、选择题（每小题3分，共30分）下列各小题均有四个选项，其中只有一个是正确的．
1．的绝对值是（ ）
A． B． C． D．
2．如图所示的搭成的几何体的左视图是（ ）

A． B． C． D．
3．英国《自然》杂志报道，德国科学家已创造出迄今最短的电子短脉冲，其持续时间仅为53阿秒，速度之快足以让显微镜捕捉到电子在原子间跳跃的图像．已知53阿秒秒，则0.000000000000000053用科学记数法表示为（ ）
A． B． C． D．
4．如图，直线，一副三角板按如图所示的方式放置，且．若，则的度数为（ ）

A．10° B．15° C．20° D．25°
5．下列计算正确的是（ ）
A． B．
C． D．
6．已知关于x的一元二次方程有实数根，则k的值不可能是（ ）
A． B．0 C．1 D．2
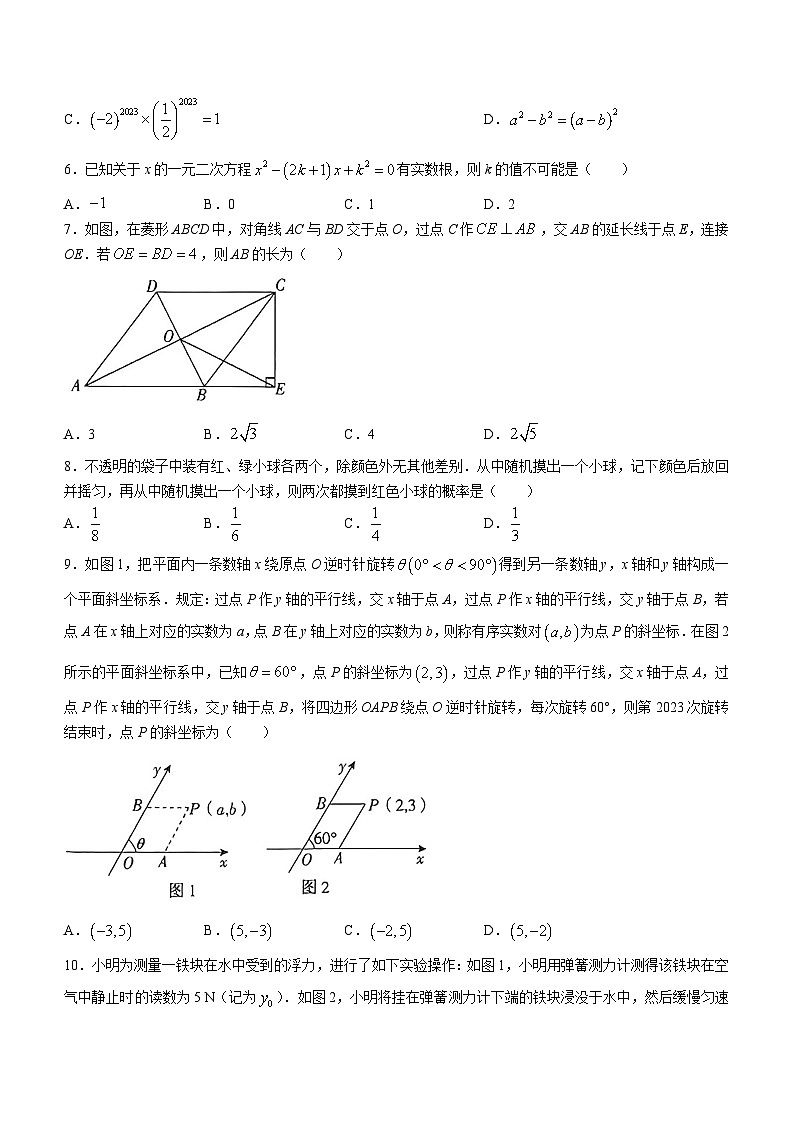
7．如图，在菱形ABCD中，对角线AC与BD交于点O，过点C作，交AB的延长线于点E，连接OE．若，则AB的长为（ ）

A．3 B． C．4 D．
8．不透明的袋子中装有红、绿小球各两个，除颜色外无其他差别．从中随机摸出一个小球，记下颜色后放回并摇匀，再从中随机摸出一个小球，则两次都摸到红色小球的概率是（ ）
A． B． C． D．
9．如图1，把平面内一条数轴x绕原点O逆时针旋转得到另一条数轴y，x轴和y轴构成一个平面斜坐标系．规定：过点P作y轴的平行线，交x轴于点A，过点P作x轴的平行线，交y轴于点B，若点A在x轴上对应的实数为a，点B在y轴上对应的实数为b，则称有序实数对为点P的斜坐标．在图2所示的平面斜坐标系中，已知，点P的斜坐标为，过点P作y轴的平行线，交x轴于点A，过点P作x轴的平行线，交y轴于点B，将四边形OAPB绕点O逆时针旋转，每次旋转60°，则第2023次旋转结束时，点P的斜坐标为（ ）

A． B． C． D．
10．小明为测量一铁块在水中受到的浮力，进行了如下实验操作：如图1，小明用弹簧测力计测得该铁块在空气中静止时的读数为5 N（记为）．如图2，小明将挂在弹簧测力计下端的铁块浸没于水中，然后缓慢匀速向上提起，直至铁块完全露出水面一定高度，整个过程中弹簧测力计的读数y（单位：N）与铁块被提起的高度x（单位：cm）之间的函数关系的大致图象如图3所示．已知与y的差值即为铁块在水中受到的浮力，则下列说法中错误的是（ ）

A．当时，弹簧测力计的读数保持不变为4 N，铁块受到的浮力保持不变为1 N
B．当时，弹簧测力计的读数越来越大，铁块受到的浮力越来越小
C．当铁块被提起的高度为5 cm时，弹簧测力计的读数为5 N
D．当时，弹簧测力计的读数保持不变为5 N，铁块已完全露出水面
二、填空题（每小题3分，共15分）
11．若一次函数的图象不经过第三象限，则整数k的值可以是______．
12．满足不等式组的最大整数解是______．
13．某水果店老板为了解甲、乙两品种草莓的品质（大小、甜度等），进行了抽样调查．在相同条件下，随机抽取了两品种草莓各7份样品，对草莓的品质进行评分（百分制），并对数据进行收集、整理，然后绘制出如下所示的两品种草莓品质得分的调查结果统计图．根据统计图，可知品质相对较好的是______品种．（填甲或乙）

14．如图，在扇形OAB中，，，点C是半径OA上一点，将扇形OAB沿BC翻折，点A的对应点为，且点恰好在BO的延长线上，则图中阴影部分的面积为______．

15．如图，在中，，，．D为斜边AB的中点，P为AC边上一动点，连接PD，将线段PD绕点D顺时针旋转90°得到线段，交BC边于点Q．当为直角三角形时，AP的长为______．

三、解答题（本大题共8个小题，共75分）
16．（1）（5分）计算：．
（2）（5分）化简：．
17．（9分）2023年春节是新型冠状病毒感染“乙类乙管”政策实施后第一个公众假期，疫情积压的探亲访友、旅游过年、民俗体验、避寒和冰雪等出游需求集中释放，奠定了全年旅游经济“高开稳增，持续回暖”的市场基础．根据文化和旅游部数据中心测算，今年春节假期全国国内旅游出游3.08亿人次．为更好地服务游客，洛阳某旅游景区管理部门在春节假期期间随机抽取了100名游客进行问卷调查（调查问卷表如图所示），并根据调查结果绘制了如下不完整的统计图表，部分信息如下：
旅游景区游客调查问卷
尊敬的游客朋友，您好，欢迎来到洛阳旅游景区！
为进一步提升景区服务质量，增强游客体验感，现邀请您对景区进行评价：
1．您对本次旅游的满意度打多少分（满分为10分）？
A．8~10分 B．6~8分 C．4~6分 D．2~4分 E．0~2分
2．在本次旅游中，您不满意的项目是【可多选】
A．交通 B．食宿 C．景观 D．服务 E．设施
谢谢您的合作，祝您生活愉快！

根据以上信息，解答下列问题：
（1）请补全条形统计图，本次调查的游客旅游满意度打分的中位数应该落在______类别．
（2）扇形统计图中“C”所在扇形的圆心角的度数为______．
（3）根据游客不满意的项目调查结果扇形统计图，请对该景区提出一条合理化建议．
18．（9分）位于河南省登封市嵩山南麓嵩岳寺内的嵩岳寺塔是中国现存最早的砖塔，也是全国古塔中的孤例．嵩岳寺塔建于北魏正光年间，历经1400多年风雨侵蚀，仍巍然屹立，也是中国唯一的一座十二边形塔．某数学小组测量嵩岳寺塔DC的高度，如图，在台阶AB底端A处用测角仪测得嵩岳寺塔顶端D的仰角为45°，在台阶AB顶端B处用测角仪又测得嵩岳寺塔顶端D的仰角为40°．已知测角仪的高度为1.5m，平台BG的高度为3m，台阶AB的坡度，图中所有点均在同一竖直平面内，点A，H与点C在同一水平线上，求嵩岳寺塔DC的高度．（结果精确到1m．参考数据：，，）

19．（9分）如图，在平面直角坐标系中，直线分别与x轴、y轴交于点A，B，与反比例函数的图象在第二象限内交于，两点，连接OC．已知，的面积为3．

（1）求反比例函数的解析式．
（2）直接写出不等式的解集．
（3）若M为线段OB上的一个动点，当的值最小时，求点M的坐标．
20．（9分）2022年10月12日，“天宫课堂”第三课在中国空间站开讲了，精彩的直播激发了学生探索科学奥秘的兴趣．某中学为满足学生的需求，充实物理兴趣小组的实验项目，决定购入A，B两款物理实验套装，其中A款套装单价是B款套装单价的1.2倍，用9000元购买的A款套装数量比用6000元购买的B款套装数量多10套．
（1）求A，B两款套装的单价分别是多少元．
（2）该中学准备购买A，B两款套装共50套，且购买A款套装的数量不少于B款套装数量的，则如何购买才能使花费最少？并求出最少费用为多少元．
21．（9分）2022年版《义务教育数学课程标准》在2022年9月1日正式投入使用，在这个课程标准中要求学生能利用尺规过圆外一点作圆的切线．下面是某数学兴趣小组在学过圆的相关知识后进行的一系列探究．
已知：如图1，PA为的切线，切点为A．
求作：的另一条切线PB，切点为B．
该数学兴趣小组的同学们展开了探究，经梳理，有以下几种作法：
作法一：以点P为圆心，PA长为半径作弧，交于点B，作直线PB，则直线PB即为所求，如图2所示．
作法二：连接OP，作线段OP的垂直平分线l，交OP于点M，以点M为圆心，MO长为半径作圆，交于点B，作直线PB，则直线PB即为所求，如图3所示．
作法三：作直线OP，过点A作OP的垂线交于点B，作直线PB，则直线PB即为所求．

根据以上信息，完成下列问题：
（1）该数学兴趣小组的某同学对根据作法二作出的图形进行了证明，过程如下：
证明：连接OB，由作图，可知OP是的直径．
∴（依据： ① ），即．
又∵OB是的半径，∴直线PB为的切线（依据： ② ）．
在上述证明过程中，“①”处应填写_______________________；“②”处应填写___________________．
（2）根据作法三，请用尺规补全图1．（保留作图痕迹）
（3）若的半径为1，，请你根据作法三作出的图形，求线段AB的长．
22．（10分）如图1是某公园内的一座拱桥．如图2是其桥拱的截面示意图，可视为抛物线的一部分．某时测得桥拱内的水面宽，桥拱顶点C到水面的距离是4 m．据调查，该河段水位在此基础上再涨0.6 m达到最高．

（1）按如图2所示建立平面直角坐标系，求桥拱截面所在抛物线的函数表达式．
（2）为迎佳节，拟在图1桥拱内壁上悬挂40 cm长的灯笼，为了安全，灯笼底部距离水面不小于1 m，请确定悬挂点的纵坐标的最小值和横坐标的取值范围．
（3）桥拱截面所在抛物线在x轴下方的部分与桥拱ACB在平静水面中的倒影组成一个新的函数图象G，如图3．将图象G向右平移个单位长度，平移后的函数图象在时，y随x的增大而减小，请直接写出m的取值范围．
23．（10分）综合与实践
综合实践课上，老师和同学们以“图形的变换”为主题开展数学活动．
（1）操作判断
如图1，将矩形纸片ABCD对折，折痕为EF，P为EF上一动点，连接PB，PC，将线段PC绕点P逆时针旋转90°得到PM，连接BM交EF于点Q，且点P在点Q的上方，过点P作交BM于点N．

根据以上操作，判断：①是______三角形；②线段BM，BQ，PQ之间的数量关系为______．
（2）迁移探究
若将矩形纸片ABCD换成正方形纸片ABCD，其他条件不变，则（1）中的结论是否仍然成立？若成立，请仅就图2的情形进行证明；若不成立，请说明理由．
（3）拓展应用
在边长为4的正方形ABCD中，点E，F分别为AD，BC的中点，EF交对角线BD于点Q，点P是EF上一动点，连接PC，过点P作PC的垂线，交直线BD于点M．若，请直接写出BM的长．
数学试题参考答案
一、选择题
1．【答案】C
【考点】绝对值．
【解析】根据负数的绝对值是它的相反数，可知的绝对值是，故选C．
2．【答案】A
【考点】几何体的三视图．
【解析】根据左视图的定义，可知该几何体的左视图为选项A所示图形，故选A．
3．【答案】B
【考点】用科学记数法表示较小数．
【解析】∵，故选B．
4．【答案】B
【考点】平行线的性质．
【解析】∵，∴．
∵，∴．∴．
∴，故选B．
5．【答案】B
【考点】整式的运算．
【解析】选项A中，，故选项A错误；
选项B中，，故选项B正确；
选项C中，，故选项C错误；
选项D中，，故选项D错误，故选B．
6．【答案】A
【考点】一元二次方程根的判别式．
【解析】∵关于x的一元二次方程有实数根，
∴，解得．∴k的值不可能是，故选A．
7．【答案】D
【考点】菱形的性质，直角三角形的性质．
【解析】根据菱形的性质，可知，，．
∵，∴．∴，故选D．
8．【答案】C
【考点】用列举法求简单事件的概率．
【解析】记两个红色小球分别为红1，红2，两个绿色小球分别为绿1，绿2．根据题意，列表如下．

红1
红2
绿1
绿2
红1
（红1，红1）
（红1，红2）
（红1，绿1）
（红1，绿2）
红2
（红2，红1）
（红2，红2）
（红2，绿1）
（红2，绿2）
绿1
（绿1，红1）
（绿1，红2）
（绿1，绿1）
（绿1，绿2）
绿2
（绿2，红1）
（绿2，红2）
（绿2，绿1）
（绿2，绿2）
由表，可知共有16种等可能的结果，其中两次都摸到红色小球的结果有4种，∴P（两次都摸到红色小球），故选C．
9．【答案】A
【考点】平行四边形的判定与性质，旋转的性质，等边三角形的判定与性质．
【解析】易知四边形OAPB为平行四边形，且，．
∵四边形OAPB绕点O逆时针旋转，每次旋转60°，∴每旋转6次为1个周期．
∵，∴第2023次旋转结束时点P的斜坐标和第1次旋转结束时点P的斜坐标相同．
记四边形OAPB第1次旋转结束时，点A，P，B的对应点分别为，，，
此时点在y轴上，过点作轴，交y轴于点E，延长交x轴于点F，
如解图所示．由旋转的性质，易知，，，轴，
∴，．
∴为等边三角形．∴．
易证四边形为平行四边形，∴，．
∴点的斜坐标为，即第2023次旋转结束时，点P的斜坐标为，故选A．

10．【答案】C
【考点】函数图象的分析．
【解析】由题图3，可知当时，y值不变为4，即弹簧测力计的读数保持不变为4 N，
∵，，∴保持不变为1 N，故选项A正确；
由题图3，可知当时，y值越来越大，即弹簧测力计的读数越来越大．
∵，是一个定值，∴越来越小，故选项B正确；
由题图3，可知当时，，
即当铁块被提起的高度为5 cm时，弹簧测力计的读数为4.5 N，故选项C错误；
由题图3，可知当时，y值不变为5，即弹簧测力计的读数保持不变为5 N．
∵，，∴，即铁块已完全露出水面，故选项D正确．
综上所述，故选C．
二、填空题
11．【答案】（答案不唯一）
【考点】一次函数的图象与性质．
【解析】根据一次函数的图象与性质，可知，∴整数k的值可以是．
12．【答案】
【考点】解一元一次不等式组．
【解析】解不等式，得；解不等式，得．
∴不等式组的解集为．∴最大整数解为．
13．【答案】甲
【考点】折线统计图．
【解析】由折线统计图，可知甲、乙两品种草莓品质得分的平均数相同，且甲品种草莓品质得分的波动较小，故品质相对较好的是甲品种．
14．【答案】
【考点】折叠的性质，全等三角形的判定与性质，直角三角形的判定与性质，扇形的面积公式，三角形的面积公式．
【解析】连接AB，过点C作于点D，如解图所示．
∵，，∴，．
由翻折，可知，．
又∵，∴．
∴．∴．∴．
∵，∴．∴．∴．
∴．

15．【答案】3或5
【考点】直角三角形的性质，旋转的性质，全等三角形的判定与性质，锐角三角函数．
【解析】由题意，可知，∴当为直角三角形时，分和两种情况进行讨论．
①当时，如解图1所示，则．
由旋转的性质，可知．∴．
∵D为AB边的中点，∴P为AC边的中点．∴．
②当时，过点P作于点E，
过点作于点F，如解图2所示．
在中，由勾股定理，可知．
∵D为AB边的中点，∴．
∵，∴可设，则．
∴．由旋转的性质，可知，．易得，
∴．∴，．
∴．易得，∴．
∴．∴．
整理，得，解得．∴．
综上所述，当为直角三角形时，AP的长为3或5．

三、解答题
16．【考点】实数的运算，分式的化简．
【答案】解：（1）原式．
（2）原式．
17．【考点】条形统计图，扇形统计图，中位数．
【答案】解：（1）补全的条形统计图如解图所示．

C．
（2）90°．
（3）景区应该提高食宿和景观服务．（答案不唯一，合理即可）
18．【考点】解直角三角形的实际应用．
【答案】解：过点E作于点M，过点F作于点N，延长AE交FN于点K，延长FB交CH于点L，如解图所示，则，．

由题意，易得，，．
设嵩岳寺塔DC的高度为，则，．
在中，，∴．
在中，，，∴，解得．
经检验，是分式方程的解，且符合实际意义．
答：嵩岳寺塔DC的高度约为36m．
19．【考点】反比例函数中k的几何意义，轴对称的性质，三角形的面积公式．
【答案】解：（1）过点C作于点H，如解图1所示，则．

∵，∴．又∵，∴．
由反比例函数中k的几何意义，可知，∴（正值已舍去）．
∴反比例函数的解析式为．
（2）或．
（3）作点D关于y轴的对称点，连接，交y轴于点M，连接DM，此时的值最小，如解图2所示．

把点，分别代入，得，，即点，．∴．
易得直线的解析式为．∴．
20．【考点】分式方程的实际应用，一元一次不等式的实际应用，一次函数的实际应用．
【答案】解：（1）设B款套装的单价是x元，则A款套装的单价是1.2x元．
由题意，得，解得．
经检验，是分式方程的解，且符合题意．∴．
答：A款套装的单价是180元，B款套装的单价是150元．
（2）设购买A款套装a套，则购买B款套装套．
由题意，可得，解得．
设购买A，B两款套装的总费用为y元，则．
∵，∴y随a的增大而增大．∴当时，y有最小值7800．∴．
答：购买A款套装10套，B款套装40套，可使花费最少，最少费用为7800元．
21．【考点】尺规作图，圆周角定理及其推论，全等三角形的判定与性质．
【答案】解：（1）直径所对的圆周角是直角；
经过半径外端，并与该半径垂直的直线是圆的切线．
（2）补全的图形如解图1所示．

（3）在解图1的基础上记AB交OP于点N，连接OB，如解图2所示．

∵PA，PB为的切线，∴．
在和中，，，
∴．∴．∵，∴．
在中，，，∴．
∴．∴．
22．【考点】二次函数的实际应用．
【答案】解：（1）由题意，得，，顶点．
设桥拱截面所在抛物线的函数表达式为．
将点代入，得，解得．
∴桥拱截面所在抛物线的函数表达式为．
（2）由题意，得悬挂点的纵坐标的最小值为．
将代入，得，解得或．
∴悬挂点的横坐标的取值范围为．
（3）．
【提示】∵抛物线的对称轴为直线，
∴图象G的对称轴也是直线，且当或时，y随x的增大而减小．
∴将图象G向右平移个单位长度后，可得平移后函数图象的对称轴是直线，
且当或时，y随x的增大而减小．
∵图象G平移后得到的函数图象中，当时，y随x的增大而减小，
∴且或．当且时，解得．
当时，解得．由题意，知，∴不符合题意，舍去．
综上所述，m的取值范围是．
23．【考点】矩形的性质，折叠的性质，旋转的性质，正方形的性质，全等三角形的判定与性质，等腰直角三角形的判定与性质．
【答案】解：（1）①等腰直角；②．
（2）仍然成立，证明如下：
由题意，可知EF垂直平分BC，∴，．∴．
由旋转的性质，可知，．∴．
∵，∴．∴．
∴．
∴．∴．∴．
∴，．∴为等腰直角三角形．
∴．∴．
（3）或．
【提示】由题意，可分两种情况进行讨论．
①当点P在点Q上方时，连接PB，过点P作交BM于点N，如解图1所示．
由（2），可知．易知，．∴．
②当点P在点Q下方时，连接PB，过点P作交BM于点N，如解图2所示．
易证，．∴．
易知，．∴．综上所述，BM的长为或．