初中数学湘教版九年级上册2.2 一元二次方程的解法课前预习课件ppt

这是一份初中数学湘教版九年级上册2.2 一元二次方程的解法课前预习课件ppt，共20页。PPT课件主要包含了情景导入，将下列各式分解因式，配方法，公式法，因式分解法，思考探究，因此原方程的根为，由此得，课堂练习，根据平方根的意义得等内容，欢迎下载使用。
(1)5x2-4x；(2)x2-4x+4；(3)4x(x-1)-2+2x；(4)x2-4；(5)(2x-1)2-x2；
我们已经学习了用配方法、公式法和因式分解法解一元二次方程，在具体的问题中，我们要根据方程的特点，选择合适的方法来求解.
解一元二次方程的三种方法
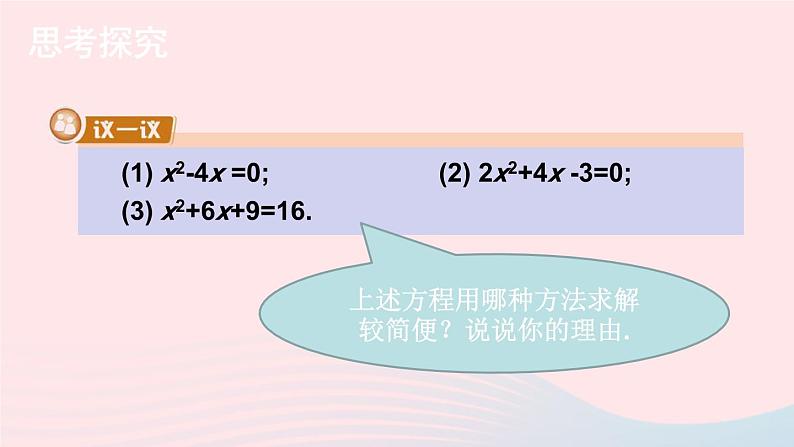
(1) x2-4x =0;(2) 2x2+4x -3=0;(3) x2+6x+9=16.
上述方程用哪种方法求解较简便？说说你的理由.
选择合适的方法解下列方程:
(1)x2+3x =0;(2)5x2-4x -1=0;(3) x2+2x -3 =0.
解:(1)将方程左边因式分解,得
由此得x =0 或x ＋3=0.
解得x1=0，x2=-3.
x ( x ＋3 )=0,
解:(2)这里a=5，b=-4，c=-1.
b2-4ac = ( -4 )2-4×5×( -1 )= 36,
解:(3)原方程可化为
x2+2x＋1-4=0,
( x ＋1 )2=4,
x＋1 =2或x+1=-2.
x1=1，x2=-3.
如何选择合适的方法来解一元二次方程呢？
总之，解一元二次方程的基本思路都是:将一元二次方程转化为一元一次方程，即降次，
ax2+ bx +c =0 ( a ≠0 )
( x+ n ) 2 =d ( d ≥ 0 )
( x -d ) ( x -h).
降次的本质是把方程 ax2+ bx +c =0 ( a≠0)的左边的二次多项式分解成两个一次多项式的乘积，即ax2+ bx + c =a ( x -x1 ) ( x -x2 )， 其中x1和x2是方程ax2+ bx +c =0的两个根.
(1)3x2 - 4x = 2x;
解:(1)原方程可化为
3x2 - 6x = 0,
将方程左边因式分解,得
由此得x =0 或x -2=0.
解得x1=0，x2=2.
3x ( x -2 )=0,
解:(2)原方程可化为
( x+3 )2=3;
解:(3)将方程左边因式分解,得
(4) x ( x-6)=2(x -8);
解:(4)原方程可化为
x2-8x+16=0;
解得x1=x2= 4.
解:(5)原方程可化为
(6) x ( x+8)=25;
解:(6)原方程可化为
x2+8x-25=0;
x2+8x+42-42-25=0;
(7) (x+2)(x-5 )=1;
解:(7)原方程可化为
x2-3x-11=0;
这里a=1，b=- 3，c=-11.
(8) ( 2x+1 )2=2(2x ＋1).
由此得2x+1=0 或2x-1=0.
解得x1= ，x2 = .
(2x ＋1)2-2(2x+1)=0,
解:(8)原方程可化为
(2x ＋1)(2x - 1)=0,