奥数五年级上册 第14讲：奇偶性 课件+教案

（ 五年级 ）                                      备课教员：××× 

第十四讲    奇偶性

一、教学目标：

1. 认识奇数和偶数 ，了解奇偶性的规律。

2. 尝试运用各种方法发现规律，运用数的奇偶性解决生活中

   的一些简单问题。

3. 经历探索加法中数的奇偶性变化的过程，在活动中发现

   加法中数的奇偶性的变化规律，在活动中体验研究方法，

   提高推理能力。

二、教学重点：

发现并掌握数的奇偶性变化规律。

三、教学难点：

应用数的奇偶性变化规律分析和解决生活中的一些简单问题。

四、教学准备：

PPT

五、教学过程：

第一课时（50分钟）

一、导入（5分)

师：同学们玩过有奖游戏吗？

生：……

师：今天老师给大家带来一个有奖游戏，游戏规则是：掷骰子，掷到几，就从

    转盘上的数下一格向前走几，走到有奖的格子奖品就归你了 。

    （图略）

师：谁想第一个来试一试？

生：……

师：在游戏中，你们发现了什么？

生：刚才这几位同学得到的都是糖，为什么得不到学习用品呢？

师：问题提的真好，有思考价值。为什么他们拿到的奖品都是糖，得不到有实

    用价值的奖品？

师：你们可以互相交流一下，看看为什么这样？

    学生交流，汇报奇数+奇数=偶数；偶数+偶数=偶数

师：你还能举些例子来证明你们的发现是正确的吗？（学生举例子证明）

师：你们能修改一下规则，让这个游戏一定能得到学习用品吗？

    引导学生发现：奇数+偶数=奇数。

【板书课题：】奇偶性

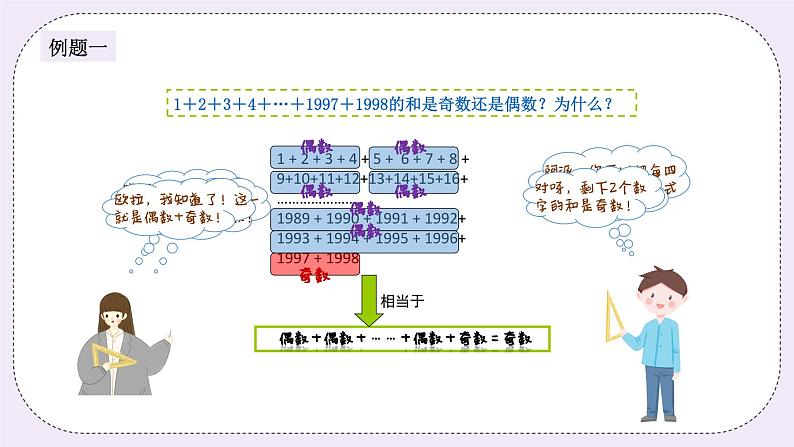
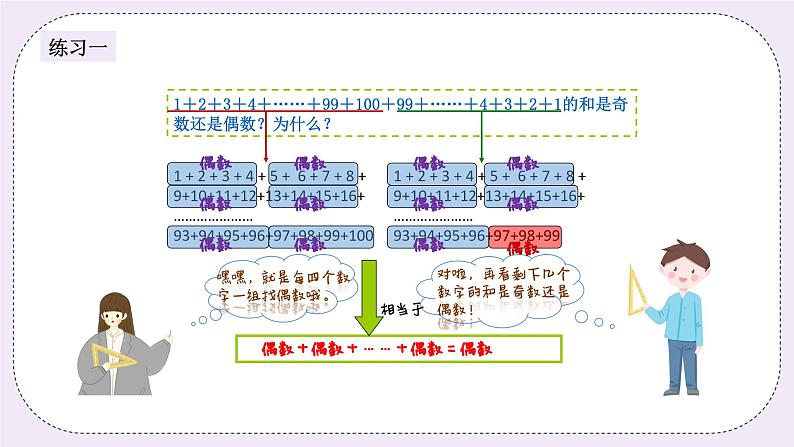
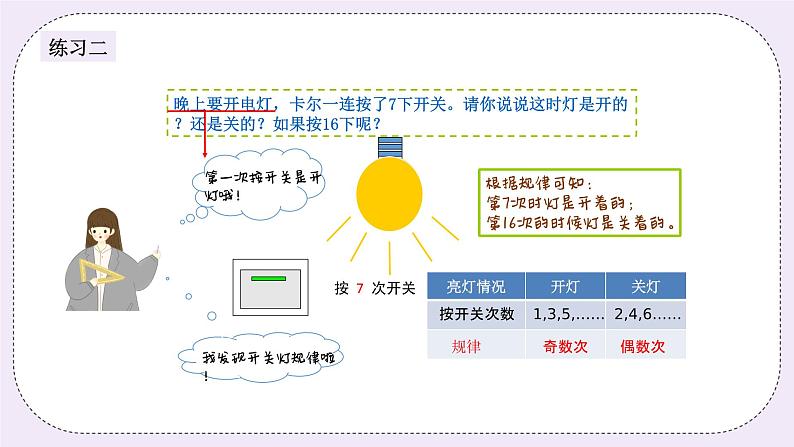
二、探索发现授课（40分）

（一）例题1：（13分）

1＋2＋3＋4＋…＋1997＋1998的和是奇数还是偶数？为什么？

 （PPT出示）

师：同学们，这么一大串数字相加，难道我们要去一个一个加出来吗？

生: 那要算到什么时候啊。

师：没错，一个一个去加是很繁琐，其实这是有方法的。

生：老师，什么方法？

师：我们把这些数字分为四个一组，（1+2+3+4）、（5+6+7+8）...(1997+1998)

    同学们，你们发现了什么？

生1：我发现四个数的和都是偶数。

生2：我发现最后两个数的和是奇数。

师：嗯，你们观察得很仔细，发现的结论也很正确。老师现在想要考考你们。

    好吗？

生：好的。

师：偶数和偶数相加的和是偶数还是奇数呀？

生：偶数。

师：是的，真棒。那偶数和奇数相加的和是偶数还是奇数呢？

生：奇数。

师：同学们都很聪明，那我们回头来看这道题目。其实就是什么呀？

生：偶数和奇数相加。

师：那它们的和是奇数还是偶数呢？

生：是奇数。

师：没错，说得真好，给自己鼓励一下。

板书：

偶数+偶数+……+偶数+奇数=奇数

答：它们的和是奇数。

 （PPT出示）

练习1：（6分）

  1＋2＋3＋4＋……＋99＋100＋99＋……＋4＋3＋2＋1的和是奇数还是偶数？为什么？

 （PPT出示）

分析：

    我们可以把这些数字四个一组，前部分可以看成（1+2+3+4）、（5+6+7+8）……（97+98+99+100），同样的后部分也可以看成（1+2+3+4）、（5+6+7+8）……最后还剩下（97+98+99）三个数，前面的四个数相加都是偶数，偶数个偶数相加还是偶数，最后97+98+99也是偶数，变成了偶数加偶数，和是偶数。  

板书：

答：这些数字的和是偶数。

 （PPT出示）

（二）例题2：（13分）

    米德和欧拉打乒乓球，欧拉开始发球，假设两人接球没有间断。

   （1）第8次接球的是米德还是欧拉？为什么？

   （2）第19次接球的是欧拉，对吗？为什么？

 （PPT出示）

师：老师问同学们，米德和欧拉，第一次接球的是谁？

生：米德。

师：没错，第一次接球的是米德。那第二次接球的就是...

生：是欧拉。

师：没错，从奇偶方面来说呢？第奇数次接球的是...

生：米德。

师：第偶数次接球的是...

生：欧拉。

师：那对于问题，我们就可以很好的解决了。第8次接球的是谁呢？我们先判

    断8是奇数还是偶数？

生：偶数。

师：那么第8次接球的就是...

生：欧拉。

师：没错，真棒。同样的，对于第二问，我们先怎么样？

生1：判断19是奇数还是偶数。

生2：19是奇数。

师：那么第19次接球的是？

生：米德。

板书：

第偶数次接球的是欧拉。

第奇数次接球的是米德。

答：第8次接球的是欧拉。第19次接球的是米德。

 （PPT出示）

练习2：（8分）

    晚上要开电灯，卡尔一连按了7下开关。请你说说这时灯是开的？还是关的？如果按16下呢？

分析：

    根据题干，可知第一次是开，第二次是关，1是奇数，2是偶数，可知奇数时开，偶数时关。7是奇数，所以按7下时灯是开的；16是偶数，所以按16下时灯是关的。

板书：

奇数时灯是开的；偶数时灯是关的。

答：连按7下时灯是开的，连按16下时灯是关掉的。

三、小结：（5分）

   奇数和偶数之间有以下性质：

   奇数＋（－）奇数＝偶数；

   奇数＋（－）偶数＝奇数；

   偶数＋（－）偶数＝偶数；

第二课时（50分）

一、复习导入（3分）

师：同学们，上节课你们学习到了什么内容呢？

生：学习了数的奇偶性。

师：你们能够更加具体的说说吗？

生：老师你先说一个。

师：好的，就比如说奇数+奇数=偶数。

生：老师，我会了。

生1：奇数＋（－）偶数＝奇数。

生2：偶数＋（－）偶数＝偶数；

师：看来同学们都掌握得不错，今天啊，我们继续研究数的奇偶性。好吗？

生：好的。

（出示PPT)

二、探索发现授课（42分）

（一）例题3：（13分）

某班同学参加学校的数学竞赛。试题共50道。评分标准是：答对一道给3分，不答给1分，答错倒扣1分。请你说明：该班同学得分总和一定是偶数。

 （PPT出示）

师：同学们，假设一个学生得满分是多少分呢？

生：50题全对，150分。

师：没错，相对于答对一题来说，漏做一题要扣多少分呢？

生：扣2分。

师：是的，你们真聪明。那相对于答对一题来说，做错一题呢？

生：不仅得不到3分，还要倒扣1分，所以是扣4分。

师：我们再来观察150、2、4是奇数还是偶数呢？

生：偶数。

师：那么我们就可以知道每位同学的得分就是？

生：偶数－偶数－……－偶数=偶数。

师：是的，该班同学的得分总和呢？

生：偶数＋偶数＋偶数＋……＋偶数=偶数。

师：真棒，看来同学们都掌握得不错。那么我们就知道该班同学得分总和是奇

    数还是偶数呢？

生：偶数。

板书：每位同学得分：   

    偶数－偶数－……－偶数＝偶数

所有同学得分总和：

    偶数＋偶数＋……＋偶数=偶数

答：该班同学得分总和是偶数。

同学们，还可以尝试用别的方法，试试看。

 （PPT出示）

练习3：（7分）

芭啦啦综合教育学校“伊嘉儿杯”数学竞赛，竞赛题30道，记分方法是：底分15分，每答对一道加5分，不答的题，每道加1分，答错一道扣1分。如果有333名学生参赛，那么他们的总得分是奇数还是偶数？

 （PPT出示）

分析：

    如果每一个人全做对可以得到15+5×30=165（分），即总分是奇数，若错一题要从中扣去5+1=6（分）（偶数），若一题不答从中扣去5-1=4（分）（偶数），也就是无论是答错或不答扣的分数都为偶数，奇数－偶数=奇数，所以一人得分总数是奇数，又因为总人数是333名，是奇数，奇数个奇数的和还是奇数，所以最终结果是奇数。

板书：15＋5×30=165（分）

5+1=6（分）

5－1=4（分）

奇数－偶数－……－偶数=奇数

奇数+奇数+……+奇数=奇数

答：他们的总得分是奇数。

 （PPT出示）

（二）例题4：（13分）

    任意给出一个五位数，将组成这个五位数的5个数字的顺序任意改变，得到一个新的五位数。那么，这两个五位数的和能不能等于99999？

 （PPT出示）

师：老师问同学们，如果有相加得99999的两个五位数，这个数会不会出现进

    位加法呢？

生：不会。

师：是的，肯定不会，如果出现进位，就不可能是99999了。

生：对的老师。

师：9是奇数，那就说明了什么？一起来思考一下。

生：所有数字加起来是45。

师：真棒，大家看，这样的两个五位数是通过改变数字排序而成的，是吗？

生：是的。

师：那说明这些数字加起来就一定是45。那么一个五位数的数字和是多少呢？

生：45÷2=22.5

师：可能是这样的吗？是小数？

生：不可能。

师：所以说这两个五位数的和不能等于99999。

板书：

9+9+9+9+9=45

45÷2=22.5

五个数字相加的和不可能是小数。

答：这两个五位数的和不能等于99999。

 （PPT出示）

练习4：（7分）

能否从四个3、三个5、两个7中选出5个数，使这5个数的和等于22？

 （PPT出示）

分析：

    3、5、7都是奇数，而选择5个数，个数5也是奇数，奇数个奇数相加的和还是奇数，不可能是偶数22。

板书：奇数个奇数相加仍然是奇数。

答：不能。

 （PPT出示）

（三）例题5（选讲）：

    是否存在自然数a、b、c，使得(a-b)(b-c)(a-c)=45327？

 （PPT出示）

师：同学们45327是奇数还是偶数呀？

生：奇数。

师：奇数要...相乘才能得到。

生：奇数相乘才能得到奇数。

师：也就是说a-b、b-c、a-c都是什么？

生：都是奇数。

师：是的，真不错。我们知道减法中，哪两个数相减会得到奇数呢？

生：奇数-偶数=奇数。

师：还有吗？

生：偶数-奇数=奇数。

师：真不错。

师：那我们再来看题目，为了满足要求，假设a是奇数，b是偶数。为了满足

    b-c是奇数，那么c就是？

生：c是奇数。

师：那么a-c是？

生：偶数。

师：所以你们发现了什么没有呢。

生：不存在自然数a、b、c，使得(a-b)(b-c)(a-c)=45327。

 （PPT出示）

板书：

假设a是奇数

那么b是偶数

那么c是奇数。

a-c是偶数。

答：不存在自然数a、b、c，使得(a-b)(b-c)(a-c)=45327。

 （PPT出示）

练习5：

    a、b、c三个数的和与它们的积的和为奇数，问这三个数中最多可以有几个奇数？  

 （PPT出示）

分析：

根据题目内容，可以列出所要讨论的式子为a+b+c+abc。则接下来可以分类讨论3奇0偶，2奇1偶，1奇2偶，0奇3偶四种情况。经验证如果要满足上式结果为奇数，那么可以发现最多只能有1个奇数。

 （PPT出示)

板书：

a+b+c+abc

当a、b、c是三个奇数时，abc也是奇数，4个奇数相加和是偶数。

当a、b、c是2个奇数1个偶数时，abc是偶数，2个奇数的和是偶数，3个偶数相加和是偶数。

当a、b、c是1个奇数2个偶数时，abc是偶数，1个奇数和3个偶数的和是奇数。

答：这三个数中最多可以有1个奇数。

 （PPT出示）

三、总结：（5分）

2，4，6，8，10，……能被2整除的自然数叫偶数。

1，3，5，7，9，……不能被2整除的自然数叫奇数。

奇数和偶数之间有以下性质：

奇数＋（－）奇数＝偶数；

奇数＋（－）偶数＝奇数；

偶数＋（－）偶数＝偶数；

奇数×（÷）奇数＝奇数；

偶数×（÷）偶数＝偶数；

偶数×（÷）奇数＝偶数。

四、随堂练习：

1. 29＋30＋31＋……＋86＋87＋88得数是奇数还是偶数？

29+30+31+32+33+34+ …+86+87+88

30个奇数+30个偶数

 结果为偶数。

答：得数是偶数。

2. 三个杯子，杯口全部朝上放在桌上。每次翻动2个杯子，经过若干次翻动，

   能否使三个杯子全部杯口朝下吗？

因为每次要翻动两个杯子，不管翻动几次，翻动的个数是2n个，是偶数，所以不可能使3个（奇数）杯子全部杯口朝下。

答：不能使三个杯子全部杯口朝下。

3. 某班同学参加学校的数学竞赛。试题共29道。评分标准是：答对一道给3

   分，不答给1分，答错倒扣1分。该同学得分是奇数还是偶数？

全部答对得29×3=87（分），不答少得3－1=2（分），答错一题少得3+1=4（分），则87减去若干个偶数，结果是奇数。

答：该同学的得分是奇数。

4. 是否存在自然数a和b，使得ab(a＋b)=115?

假设存在，115是奇数，奇数和奇数相乘得到奇数，也就是说ab和a+b均是奇数，因为要满足ab是奇数，那么a、b都是奇数，因此a+b是偶数，奇数和偶数相乘是偶数，这就产生了矛盾。

答：不存在自然数a和b，使得ab（a+b）=115。

5. 已知a,b,c中有一个是511，一个是622，一个是793。求证：

   是一个偶数。

若a是511，则a－1是偶数；b是622，则b－2是偶数；c=793，则c－3是偶数，所以（a-1）（b-2）（c-3）是偶数；b=793，则b-2是奇数；c=622，则c-3是奇数，所以（a-1）（b-2）（c-3）是偶数；

若a是622，则a－1是奇数；b是511，则b－2是奇数；c=793，则c－3是偶数，所以（a-1）（b-2）（c-3）是偶数；b=793，则b-2是奇数；c=511，则c-3是偶数，所以（a-1）（b-2）（c-3）是偶数；

若a是793，则a－1是偶数；b是622，则b－2是偶数；c=511，则c－3是偶数，所以（a-1）（b-2）（c-3）是偶数；b=511，则b-2是奇数；c=622，则c-3是奇数，所以（a-1）（b-2）（c-3）是偶数；

答：（a-1）（b-2）（c-3）是一个偶数。

家庭作业

主管评价

主管评分

课后反思

（不少于60字）

整体效果

设计不足之处

设计优秀之处