奥数五年级上册 第13讲：最值问题 课件+教案

五年级                                      备课教员：××× 

第十三讲    最值问题

一、教学目标：

1.能找出题目中隐藏的限制条件，会运用限制条件去分析最

  大最小的问题。

2. 锻炼从限制条件中去分析问题的能力，锻炼知识综合运用

  的能力。

3. 感受数学与生活的密切联系，提高学习数学的兴趣和学好

  数学的信心。

二、教学重点：

1.学会在题目中判断出限制条件。

2.从限制条件中去分析最大最小问题。

三、教学难点：

1.对所学知识的综合运用。

2.从限制条件中去分析最大最小问题。

四、教学准备：

PPT

五、教学过程：

第一课时（50分钟）

一、导入（5分)

师：同学们，芭啦啦综合教育学校对米德等人进行了测试。你们想不想知道他

    们都得了多少分呢？

生：想。

师：阿派、米德、欧拉、卡尔、阿尔法五个人的平均分是92分，他们五个人中

    最低分是75分，阿派是第三名。

生：那阿派是几分呀？

师：他们五个人分数都不同，你们能算出阿派至少是几分吗？

生：能。

师：真棒，那拿起笔试试吧。

【板书课题：】最值问题

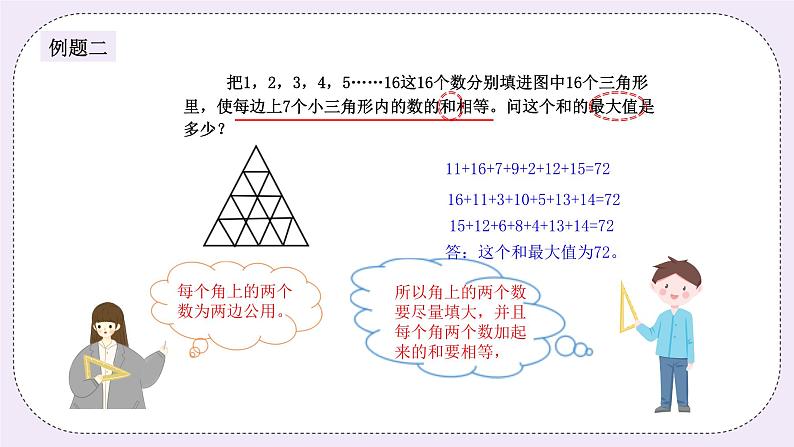
二、探索发现授课（40分）

（一）例题1：（13分）

三个老师为7位不同的扮演者化妆，这7位同学化妆需要的时间分别为8、12、14、17、18、23、30分钟。如果三位老师化妆速度相同，问最少经过多少时间完成化妆任务？

 （PPT出示）

师：同学们，如果不单独化妆，你们知道理论上需要几分钟吗？

生: （8+12+14+17+18+23+30）÷3=40……2(分钟)，应该是40分钟的样子。

师：是的，你真棒！

师：但是现在因为要单独化妆，你们认为我们应该怎么分配这三位老师？

生：应该使时间最接近40分钟，才会使时间最短。

师：没错，你说得真好！那具体该怎么分呢？

生：18+23=41（分钟）；30+12=42（分钟）；8+14+17=39（分钟）。

师：很棒，看来你们都很聪明。

板书：

 （8+12+14+17+18+23+30）÷3=40……2(分钟)

  18+23=41（分）；30+12=42（分钟）；8+14+17=39（分钟）

答：最少经过42分钟完成化妆任务。

 （PPT出示）

练习1：（6分）

    山姆大叔机床公司需要维修7辆卡车，如果派一名工人维修，这7辆卡车修复需要的时间分别为12,17,8,18,23,30和40分钟，现在由3名工作效率相同的维修工各自独立工作，最快多少分钟可以完成任务？

 （PPT出示）

分析：

   如果不单独维修，理论上需要（12+17+8+18+23+30+40）÷3=49……1（分钟），现在由3名维修工单独维修，我们只需将卡车分为3组，使之最接近49即可。

板书：

  （12+17+8+18+23+30+40）÷3=49……1（分钟）

  分为3组，使时间最接近平均数：

  12+40=52（分钟）；30+18=48（分钟）；17+8+23=48（分钟）

答：最快52分钟可以完成任务。

 （PPT出示）

（二）例题2：（13分）

把1，2，3，4，5……16这16个数分别填进图中16个三角形里，使每边上7个小三角形内的数的和相等。问这个和的最大值是多少？

 （PPT出示）

师：同学们，我们看大三角形，每个角的两个数是不是有两条边共用？

生：是的。

师：那为了使每条边的和相等且最大，你们认为角上的数应该怎么填呢？

生：填大的数，并且加起来要相等。

师：是的，真棒。那我们看看满足条件的3组数是什么呢？

生：11和16；12和15；13和14。

师：哇，说得真好。这三组的和都为27，我们把它填在三个角的两个小三角形

    内。

师：你们认为1填在哪里呢？

生：填在最中间的小三角形内。

师：没错，真有想法。我们再来看看2到10，它们的总和是多少呢？

生：54。

师：没错，那我们就可以知道每边的平均数是54÷3=18。

生：我知道了，满足这样条件的三组数分别为：(2、6、10),(3、7、8),(4、5、

    9),将这三组数分别添入每边中间的三个小三角形内。

师：同学们都很会思考，那按照上述方法,每边和都是72,而且最大。

（说明：可能有其它添法,但是满足相等条件下和最大,这个和肯定是72）

板书：

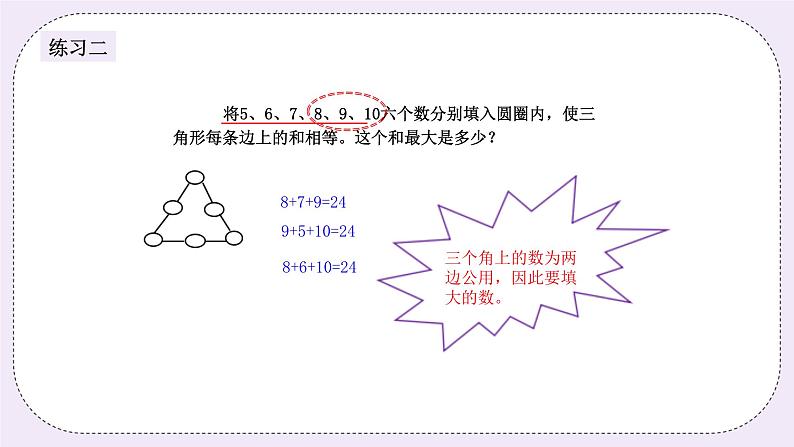
  11+16+7+9+2+12+15=72

 16+11+3+10+5+13+14=72

 15+12+6+8+4+13+14=72

答：这个和最大值为72。

还有其他的方法，大家想一想。

（PPT出示）

练习2：（8分）

将5、6、7、8、9、10六个数分别填入圆圈内，使三角形每条边上的和相等。这个和最大是多少？

 （PPT出示）

分析：

    三个角上的数为两边共有，所以应填最大的三个数，再根据每边上的和要最大，将5、6、7填入圆圈内。

板书：

  8+7+9=9+5+10=8+6+10=24

答：这个和最大是24。

 （PPT出示）

三、小结：（5分）

    在数学中，常出现一些在自然数范围内变化的量的最值问题，我们称之为离散最值问题。解决这类非常规问题，大致可从以下几个方面着手：  

    1.着眼于极端情形；

    从极端情形入手，着眼于极端情形，是求解最值问题的有效手段。   

    2.枚举比较——确定最值；

    当我们在有限数中求最大（或最小）值时，枚举法是常用的基本方法之一。这种方法的大意是：将问题所涉及的对象一一列出，逐一比较从中找出最值；或者将与问题相关的各种情况逐一考察，最后归纳出需要的结论。

第二课时（50分）

一、复习导入（3分）

师：同学们，谁能说说在上节课你有什么收获？

生：通过上节课的学习，我大致了解了最值问题的解决方法。

师：恩，不错，说明你有学到新知识。

生：......

师：那我们这节课继续学习最值问题，加深对最值问题的理解，好吗？

生：好的！

（出示PPT)

二、探索发现授课（42分）

（一）例题3：（13分）

有8个西瓜，它们的重量分别是2千克、3千克、4千克、4千克、5千克、6千克、8.5千克、10千克。把它们分成三堆，要使最重的一堆西瓜尽可能轻些，那么，最重的一堆应是多少千克？

　（PPT出示）

师：同学们，题目中说要让最重的一堆西瓜尽可能轻，另外一个意思是不是就

　　是说分成的三堆重量要尽量平均分呀？

生：是的！

师：真棒，老师一点拨就理解了。

师：我们可以先求出这堆西瓜的总重量，再求出平均分成3堆的重量是多少。

生：（2+3+4+4+5+6+8.5+10）÷3=14……0.5（千克）

师：也就是说分成3堆，每堆的重量接近14，而最重的那一堆一定是超过这个值，而又最接近14对吗？可以理解吗？

生：可以理解。

师：非常好。那么我们可以写出答案了。

板书：

  （2+3+4+4+5+6+8.5+10）÷3=14(千克)……0.5（千克）

  2+4+8.5=14.5（千克）

  3+5+6=14（千克）

 4+10=14（千克）

答：最重的一堆是14.5千克。

 （PPT出示）

练习3：（7分）

    五位同学捐款，他们捐的钱有3张1元的，4张2元的，3张5元的和3张10元的。这五位同学捐款数各不相同，问：捐款最多的同学至少捐了多少元？

 （PPT出示）

分析：

    先求出捐款的平均数，捐款最多的同学捐的款一定大于平均数而又最接近平均数。

板书：

 （3×1+4×2+3×5+3×10）÷5=11.2（元）

  由于五个人的捐款各不相同，所以5个人捐款最理想的搭配是：12、11、10、9、8。但是总和小于56。将捐款最多钱数提高到13元，最理想的搭配是13、12、11、10、9，总和小于56。剩下的一元钱只能加到捐款数最多的钱数中，若加到其他人中，就会出现捐款数相同的情况。

  10+2+2=14（元）

  10+2=12（元）

  10+1=11（元）

  5+5=10（元）

  5+1+1+2=9（元）

答：捐款最多的同学至少捐了14元。

（PPT出示）

（二）例题4：（13分）

    一次数学考试满分100分，6位同学平均分为91分，且6人分数互不相同，其中得分最少的同学仅得65分，那么排第三名的同学至少得多少分？（分数取整数）。

（PPT出示）

师：要使第三名同学的分数最少，那么其他同学的分数要怎么样？

生：其他同学的分数要最多。

师：没错，说得很好。我们先求出这6位同学的总分。

生：91×6=546（分）。

师：是的，其他同学分数要尽量多，那么你们觉得第一名、第二名是几分？

生：100分和99分。

师：很好，现在还剩下哪几名同学的分数我们不知道？

生：第三名、第四名、第五名。

师：没错，现在我们看看第三。第四、第五的总分是多少。再求出它们的平均

    分。

生：546－100－99－65=282（分）；282÷3=94（分）。

师：那么要让第四、第五尽量大，分别为94、93，所以第三名是多少呢？

生：95分。

师：没错，真棒。掌声送给自己。

板书：

  91×6=546（分）

 546－100－99－65=282（分）

  282÷3=94（分）

答：得分排在第三名的同学至少得95分。

（PPT出示）

练习4：（7分）

    一次考试满分100分，5位同学平均分是90分，且每个人得分是不相同的整数。已知得分最少的人得了75分，那么，第一名同学至少得了多少分？

（PPT出示）

分析：

剩余的4人的平均分是93.75， 那么第一名同学一定是大于平均数的，题目中要使得第一名同学成绩越小，那么其他名次成绩要越大，又因为每个人得分是不相同的整数，若第一名是94分，则剩余的最大是93、92、91，显然平均分不会大于93.75，若第一名是95分，剩余最大的是94、93、92分，也排除，第一名最少是96分，符合题意，92、93、94、或91、93、95。  

板书：

90×5-75=375（分）

375÷4=93.75（分）

若第一名是94分，不符合题意。

若第一名是95分，也不符合题意。

若第一名是96分，符合题意的有：92分，93分，94分或者91分、93分、95分。

答：第一名至少得96分。

（三）例题5（选讲）：

    A、B、C是三个风景点，从A出发经过B到达C要走18千米，从A经过C到B要走16千米，从B经过A到C要走24千米。相距最近的是哪两个风景点？它们之间相距多少千米？

（PPT出示）

师：同学们，A、B之间的距离我们用AB表示；那谁能表示B和C以及A和C

    之间的距离呢？

生：BC。

生：AC。

师：很好。

师：那我们看题目，从A出发经过B到达C要走18千米，我们就可以用AB+BC=18

    来表示。

生：我知道了，从A经过C到B要走16千米，就可以用AC+BC=16来表示。

生：从B经过A到C要走24千米，就可以用AB+AC=24来表示。

师：同学们都很棒。一点就通。接下来一下我们把三个等式相加，可以得出

    AB+BC+CA+AB+BC+CA=18+16+24，所以可以得出AB+BC+CA，谁来说说？

生：AB+BC+CA=（18+16+24）÷2=29。

师：对比这些等式，我们可以求出AB等于多少？

生：AB=29－16=13（千米）。

师：BC呢？

生：BC=29－24=5（千米）。

师：CA呢？

生：CA=29－18=11（千米）。

板书：

  AB+BC=18（千米）

  AC+BC=16（千米）

  AB+AC=24（千米）

  AB+BC+CA=(18+16+24)÷2=29（千米）

  AB=29－16=13（千米）

  BC=29－24=5（千米）

  CA=29－18=11（千米）

答：相距最近的是B、C两个风景点，距离为5千米。

（PPT出示）

练习5：

    米德骑车到A、B、C三个景点去旅游，如果从A地出发经过B地到C地，共行10千米；如果从B地出发经过C地到A地，共行13千米；如果从C地出发经过A地到B地，共行11千米，则距离最短的两个景点间相距多少千米？

 （PPT出示）

分析：

    先求出AB+BC+CA的距离和，然后再分别求出三条线段的长度比较即可得出答案。

板书：

  因为，AB+BC=10（千米），BC+CA=13（千米），CA+AB=11（千米）

  所以，AB+BC+CA=(10+13+11)÷2=17（千米）

  AB=17－13=4（千米）

  BC=17－11=6（千米）

  CA=17－10=7（千米）

答：A、B两个景点之间距离最短，为4千米。

（PPT出示）

三、总结：（5分）

在数学中，常出现一些在自然数范围内变化的量的最值问题，我们称之为离散最值问题。解决这类非常规问题，尚无统一的方法，对不同的题目要用不同的策略和方法，就具体的题目而言，大致可从以下几个方面着手：  

1. 着眼于极端情形；

从极端情形入手，着眼于极端情形，是求解最值问题的有效手段。   

2. 枚举比较——确定最值；

当我们在有限数中求最大（或最小）值时，枚举法是常用的基本方法之一。这种方法的大意是：将问题所涉及的对象一一列出，逐一比较从中找出最值；或者将与问题相关的各种情况逐一考察，最后归纳出需要的结论。

四、随堂练习：

1. 在期中测试中，阿派语文和数学平均成绩是96分，数学和英语平均成绩是

   88分，语文和英语平均成绩是86分。求阿派的这三门功课哪门得分最高，

   是多少分？

  语文和数学的总分是：96×2=192（分） 

  语文和英语的总分是：86×2=172（分） 

  数学和英语的总分是：88×2=176（分） 

  192－172=20（分）

  英语：（176－20）÷2=78（分）

  数学：78+20=98（分）

  语文：192－98=94（分）

答：阿派这三门功课数学得分最高，得分为98分。

2. 把2~9分别填入下图圆圈内，使每个大圆上的五个数的和相等，并且最

   大。最大为多少？

  中间两个数填7、9

  7+9+3+5+6=7+9+8+2+4=30

答：最大为30。

3. 一把钥匙只能开一把锁。现有9把钥匙和9把锁，但不知道哪把钥匙开哪把

   锁。最多要试开多少次才能配好全部钥匙和锁？

  8+7+6+5+4+3+2+1=36（次）

答：最多要36次才能配好全部钥匙和锁。

4. 一次考试满分100分，6位同学平均分是90分，且各人得分是不相同的整数。

   已知得分最少的人得了75分，那么，第五名同学至少得了多少分？

  6×90-75=465（分）

  465－100－99－98－97=71（分）

  因为第6名是75分，所以第5名至少得了76分。

答：第五名同学至少得了76分。

5. 阿派家的小区里有3处游乐场，分别是A、B、C，从A出发经过B到达C要

   走36千米，从A经过C到B要走32千米，从B经过A到C要走48千米。

   相距最近的是哪两个游乐场？它们之间的距离是多少？

AB+BC=36（千米），AC+BC=32（千米），AB+AC=48（千米）

(AB+BC+AC)÷2=（36+32+48）÷2=58（千米）

AB=58－32=26（千米）

BC=58-48=10（千米）

AC=58－36=22（千米）

答：相距最近的是B、C两个游乐场，它们之间的距离是10千米。

家庭作业

主管评价

主管评分

课后反思

（不少于60字）

整体效果

设计不足之处

设计优秀之处