





还剩9页未读,
继续阅读
《复习题勾股定理》PPT课件1-八年级上册数学北师大版
展开
这是一份《复习题勾股定理》PPT课件1-八年级上册数学北师大版,共17页。
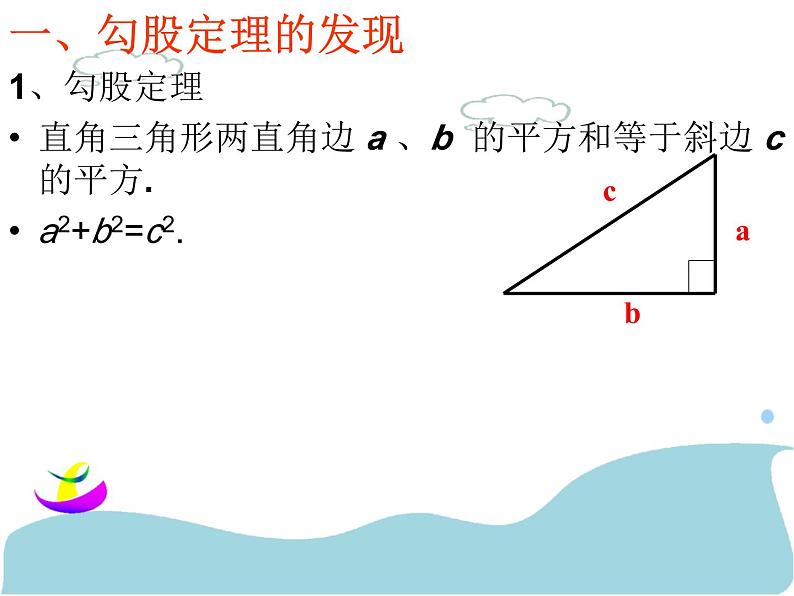
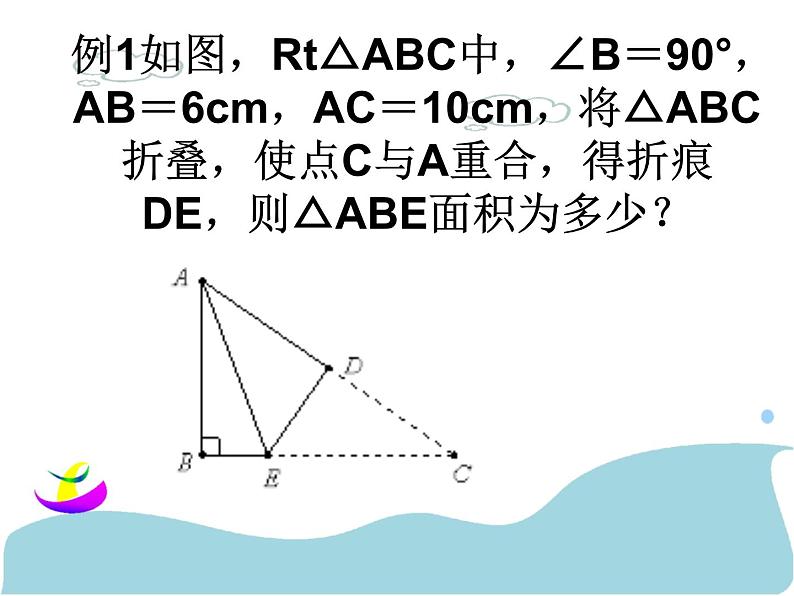
勾股定理的复习北师大版数学八年级上册1、勾股定理直角三角形两直角边 a 、b 的平方和等于斜边 c 的平方. a2+b2=c2.一、勾股定理的发现勾股定理的应用一 如图,一次“台风”过后,一根旗杆被台风从离地面3米处吹断,倒下的旗杆的顶端落在离旗杆底部4米处,那么这根旗杆被吹断裂前至少有多高?ABC34一根竹子AB原高10米,在点C处折断,竹稍A触及地面D处时,点D离竹根B有4米,试问折断处离地面有多高? 应用一 折叠 折叠和轴对称密不可分,利用折叠前后图形全等,找到对应边、对应角相等便可顺利解决折叠问题 例1如图,Rt△ABC中,∠B=90°,AB=6cm,AC=10cm,将△ABC折叠,使点C与A重合,得折痕DE,则△ABE面积为多少? 1: 已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为多少? 应用二 最短路线 1. 几何体的表面路径最短的问题,一般展开表面成平面。 2.利用两点之间线段最短,及勾股定理求解。例2: 如图,一长方体底面宽AN=5cm,长BN=10cm,高BC=16cm.D为BC的中点,一动点P从A点出发,在长方体表面移动到D点的最短距离是 葛藤是一种刁钻的植物,它绕树盘升的路线总是沿最短路线--螺旋前进的,难道植物也懂数学? 通过阅读以上信息,解决下列问题:(1)如果树干的周长(即图中圆柱体的底面周长)为30cm,绕一圈升高(即圆柱的高)40cm,则它爬行一圈的路程是多少? (2)如果已知树干高200cm,底面周长不变,葛藤自A点起缠绕而上,绕五周后其末端恰好到达B处,则葛藤最短长度是多少?AB二、勾股定理的逆定理若一个三角形三边长a、b、c满足 a2+b2=c2, 则这个三角形为直角三角形。1、已知:如图,AB=4,BC=3,∠B=90°,AD=13,CD=12,求四边形ABCD的面积谢谢
勾股定理的复习北师大版数学八年级上册1、勾股定理直角三角形两直角边 a 、b 的平方和等于斜边 c 的平方. a2+b2=c2.一、勾股定理的发现勾股定理的应用一 如图,一次“台风”过后,一根旗杆被台风从离地面3米处吹断,倒下的旗杆的顶端落在离旗杆底部4米处,那么这根旗杆被吹断裂前至少有多高?ABC34一根竹子AB原高10米,在点C处折断,竹稍A触及地面D处时,点D离竹根B有4米,试问折断处离地面有多高? 应用一 折叠 折叠和轴对称密不可分,利用折叠前后图形全等,找到对应边、对应角相等便可顺利解决折叠问题 例1如图,Rt△ABC中,∠B=90°,AB=6cm,AC=10cm,将△ABC折叠,使点C与A重合,得折痕DE,则△ABE面积为多少? 1: 已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为多少? 应用二 最短路线 1. 几何体的表面路径最短的问题,一般展开表面成平面。 2.利用两点之间线段最短,及勾股定理求解。例2: 如图,一长方体底面宽AN=5cm,长BN=10cm,高BC=16cm.D为BC的中点,一动点P从A点出发,在长方体表面移动到D点的最短距离是 葛藤是一种刁钻的植物,它绕树盘升的路线总是沿最短路线--螺旋前进的,难道植物也懂数学? 通过阅读以上信息,解决下列问题:(1)如果树干的周长(即图中圆柱体的底面周长)为30cm,绕一圈升高(即圆柱的高)40cm,则它爬行一圈的路程是多少? (2)如果已知树干高200cm,底面周长不变,葛藤自A点起缠绕而上,绕五周后其末端恰好到达B处,则葛藤最短长度是多少?AB二、勾股定理的逆定理若一个三角形三边长a、b、c满足 a2+b2=c2, 则这个三角形为直角三角形。1、已知:如图,AB=4,BC=3,∠B=90°,AD=13,CD=12,求四边形ABCD的面积谢谢









