中职高教版（2021）2.3 一元二次不等式教案

授课题目

2.3 一元二次不等式

选用教材

高等教育出版社《数学》

（基础模块上册）

授课

时长

3 课时

授课

类型

新授课

教学提示

本课从一元二次方程和二次函数之间的关系入手，引导学生借助一元二次方程的根和二次函数的图像求解一元二次不等式．

教学目标

能知道二次函数的图像，会分析一元二次方程的解与一元二次不等式的解集之间的关系，逐步提高直观想象和和逻辑推理等核心素养；能根据情况，选择求根公式法、因式分解法或配方法等求解一元二次方程， 结合二次函数的图像解一元二次不等式，逐步提高数学运算、直观想象

和逻辑推理等核心素养．

教学重点

二次函数、一元二次方程与一元二次不等式三者之间的联系，一元二次

不等式的解法

教学

难点

一元二次不等式的解法

教学

环节

教学内容

教师

活动

学生

活动

设计

意图

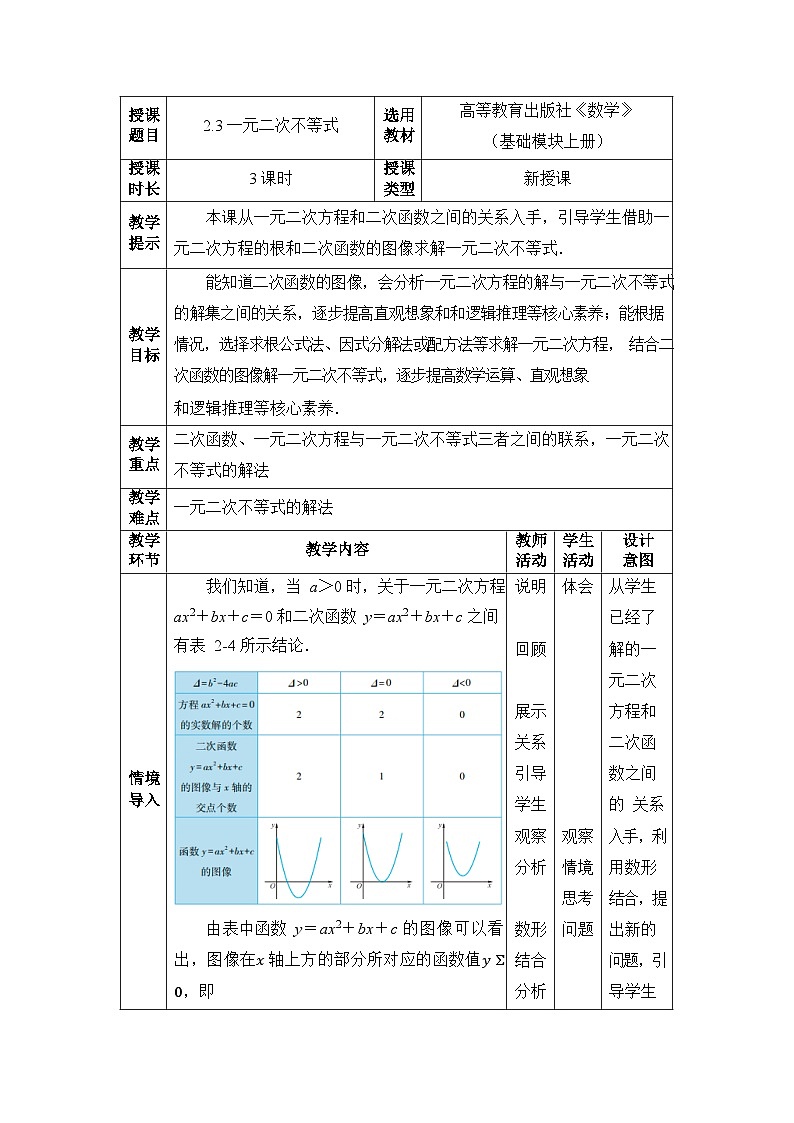
我们知道，当 a＞0 时，关于一元二次方程

ax2＋bx＋c＝0 和二次函数 y＝ax2＋bx＋c 之间有表 2-4 所示结论．

由表中函数 y＝ax2＋bx＋c 的图像可以看出，图像在?轴上方的部分所对应的函数值? Σ 0，即

说明

体会

从学生

已经了

回顾

解的一

元二次

展示

方程和

关系

二次函

情境

引导

数之间

导入

学生

的 关系

观察

观察

入手，利

分析

情境

用数形

思考

结合，提

数形

问题

出新的

结合

问题，引

分析

导学生

ax2＋bx＋c＞0，

图像在?轴下方的部分所对应的函数值? € 0， 即

ax2＋bx＋c＜0．

像这样，含有一个未知数，并且未知数的最高次数为 2 的不等式，称为一元二次不等式．其一般形式为

ax2  bx  c  0 （ a  0 ）．

上面不等式中的“  ”也可以换成“  ”、“≥”或

“≤”.

如，x2  9  0 ，3x2  2x 10 ，2x2  5x  4  0

等都是一元二次不等式．

我们知道，一元二次不等式与一元二次方程、二次函数形式上很接近，关系很密切，那么我们是能否借助它们之间的关系求解形如

ax2＋bx＋c＜0 或 ax2＋bx＋c＞0

这样的一元二次不等式呢？

主动思

说明

计算

考，培养

分析

学生直

判断

观想象、

逻辑推

理等核

心素养．

举例

提问

引导

学生

思考

下面就先来尝试分析一元二次不等式x2  2x  3  0 和二次函数 y  x2  2x  3 、一元二次方程 x2  2x  3=0 之间的关系.

如图(1)所示，二次函数 y  x2  2x  3 的图像与 x 轴交于两点，方程 x2  2x  3=0 的解是x1  1，x2  3 ，也就是抛物线与 x 轴交点(-1,0)和

(3,0)的横坐标．

提出

师生通

要求

体会

过具体

的实例，

共同总

数形

观察

结二次

探索

结合

函数、一

新知

分析

元二次

问题

方程与

一元二

次不等

思考

式三者

之间的

从图中我们可以看出，抛物线与 x 轴的两点交点将 x 轴分成了三部分．

如图(2)所示，当-1<x<3 时，函数的图像位于 x 轴的下方，此时 y<0.

如图(3)所示，当 x<-1 或 x>3 时，函数的图像位于 x 轴的上方，此时 y>0.

由此得到，不等式 x2  2x  3  0 的解集为(- 1,3)；不等式 x2  2x  3  0 的解集为(-∞，-1)∪ (3,+∞)．

按照上面的分析，我们就可以得到一般的一元二次不等式 ax2＋bx＋c＞0(a>0)和 ax2＋bx

＋c<0(a>0)的求解方法：

先求出一元二次方程的根，再根据二次函数图象与 x 轴的相关位置确定一元二次不等式的解集．

根据一元二次方程判别式的不同取值情况， 将二次函数图像、一元二次方程的解和一元二次不等式的解集列表如下，见下表，假设 x1  x2 .

强调

关系，并

利用数

形结合

进一步

解释

来分析

分析

和解决

问题，归

纳总结

归纳

领会

出一元

总结

二次不

等式的

解法，培

养学生

直观想

象、逻辑

推理和

数学抽

总结

象等核

记忆

心素养

例 1 求下列一元二次不等式的解集：

提问

观察

通过例

例题

（1） x 2  x  6  0 ；（2） x(x  3)  0 ；

题帮助

辨析

（3） 2x2  4x  3  0．

学生掌

握一元

解（1）因为不等式的二次项系数 1＞0，对应方

程 x2  x  6=0 的解为x =  2,x   3 ，对应的二次函

1 2

数的图像如图所示．所以不等式 x 2  x  6  0 的解集为(-2,3)．

（2）因为不等式的二次项系数为 1>0，对应方程 x(x-3)=0 的解为x1=0,x2  3 ，对应的二次函数的图像如图所示．所以不等式 x(x  3)  0 的解

集为,0 3,  ．

（3）因为不等式的二次项系数为 2>0，对应方程2x2  4x 3=0无实数根

（  42  4 2 3  8  0 ），对应二次函数图像如图所示，所以不等式2x2  4x  3  0 的解集为 ．

例2 若 3x2  2x 1 有意义，试求 x 的取值范围．

引导

二次不

分析

思考

等式的

解法，培

养学生

数形

求解

的数学

结合

运算、直

得到

观想象

结论

和逻辑

推理等

核心素

提问

观察

养

引导

思考

分析

数形

结合

得到

求解

结论

提问

引导

观察

分析

数形

结合

思考

得到

结论

解 要使 3x2  2 x  1 有意义， x 应该满足不等式

3x2  2x 1≥0 ．

因为不等式的二次项系数 3>0，对应方程

3x2  2 x  1  0 的解为x   1 ,x   1，对应的二次函

1 3 2

数图像如图所示，所以不等式3x2  2x 1≥0 的

解集为(,  1] [1, ) ．

3

即当 x (,  1] [1, ) 时， 3x2  2x 1 有

3

意义．

探究与发现

如何求解一元二次不等式

ax2  bx  c  0(a  0) ？

当二次项系数 a＜0 时，由不等式的性质， 不等式两边同乘−1，不等号方向改变，就可以将

a＜0 的情形转化为 a＞0 的情形，得到与原不等式同解的不等式，然后求解即可．

例 3 求一元二次不等式 x2  4 x  2  0 的解集． 解 因为不等式的二次项系数为-1<0，所以将不等式的两边同乘1，不等号方向改变，得到与原不等式同解的不等式

x2  4x  2  0 ，

其 对 应 方 程 x2  4x  2=0 的 解 为

x1  2    2 ,x2 = 2+   2 ，对应的二次函数图像如图

提问

求解

引导

思考

分析

分析

数形

结合

求解

得到

结论

提问

思考

引导

分析

分析

点明

要点

理解

解决

问题

提问

思考

引导

分析

分析

所示．

所以不等式 x2  4x  2  0 的解集为

（-,2-  2)(2+ 2，+)．

数形

结合

求解

即不等式x2  4x  2  0 的解集为

得到

（-,2-  2)(2+ 2，+)．

结论

练习 2.3

通过练

1 ．不等式  x  2 x  3  0 的解集为

习及时

  ．

掌握学

生的知

A．，2  3，  B．，2] [3， )

提问

思考

识掌握

C．[2, 3] D． 2，3

情况，查

2． 不等式2 x  x2 > 0 的解集为（ ）．

漏补缺

巩固

A． ,0 2,  B． 0, 2

练习

C． 0,2 D． R

动手

3． 不等式 x2  2x 1 0 的解集为（ ）．

巡视

求解

A．1 B． ,1  1, 

C．R D． 

4．求下列一元二次不等式的解集：

（1） 5x2  x  6  0 ； （2） x2  3x 10 ≥0 ；

（3） 2 x2  5 x  3  0 （4） 2x  x2  3  0 ．

（5）x2  2x 1  0 ； （6）4x2 12x  9  0 ；

指导

交流

（7） x2  3x  5  0 ；（8） 2x  x2  3  0．

5．当 x 在什么范围取值时， x2  3x 有意义？

6．若一元二次方程 x2  mx  1  0 无实数解，

求m的取值范围．

培养学

引导

反思

生总结

归纳

总结

总结

交流

学习过

程能力

1.书面作业：完成课后习题和学习与训练；

巩固提

布置

2.查漏补缺：根据个人情况对课堂学习复习回

高，查漏

作业

顾；

说明

记录

补缺

3.拓展作业：阅读教材扩展延伸内容．