2022-2023学年天津市第一中学高二下学期期末数学试题含答案

2022-2023学年天津市第一中学高二下学期期末数学试题

一、单选题

1．已知集合，，则（   ）

A． B．

C． D．

【答案】B

【解析】求出集合、，利用交集的定义可求得集合.

【详解】，，因此，.

故选：B.

2．已知命题，，则为（    ）．

A．， B．，

C．， D．，

【答案】B

【分析】“存在一个符合”的否定为“任意一个都不符合”

【详解】“存在一个符合”的否定为“任意一个都不符合”，故为，.

故选：B

3．设，则“”是“”的

A．充分而不必要条件 B．必要而不充分条件

C．充要条件 D．既不充分也不必要条件

【答案】D

【详解】若，则，故不充分；若，则，而，故不必要，故选D.

【解析】本小题主要考查不等式的性质，熟练不等式的性质是解答好本类题目的关键.

4．的展开式中的系数为（    ）

A．85 B．5 C．-5 D．-85

【答案】A

【分析】求出的展开式的通项，再令的指数等于和，即可得解.

【详解】的展开式的通项为，

则，，

从而的展开式中的系数为．

故选：A．

5．已知函数，则曲线在点处的切线方程为（    ）

A． B． C． D．

【答案】C

【分析】求出函数的导函数即可求出，再根据点斜式求出切线方程；

【详解】解：∵的导数为，

∴．∵，∴曲线在点处的切线方程为，即．

故选：C．

6．已知x＝2为函数f（x）＝x3﹣ax的极小值点，则f（x）的极大值为（    ）

A．﹣16 B．16 C．4 D．﹣4

【答案】B

【分析】根据x＝2为函数的极值点可得，从而求出，根据极值的定义即可求出极大值.

【详解】由，所以，

为函数的极小值点，

，即，解得,

，令

 解得或，

令，解得或，

所以函数的单调递增区间为和

令，解得，

所以函数的单调递减区间为

即为函数的极大值点，

 故选：B

【点睛】本题考查了函数的极值，需掌握函数极值的定义，解题的关键是求导函数，属于基础题.

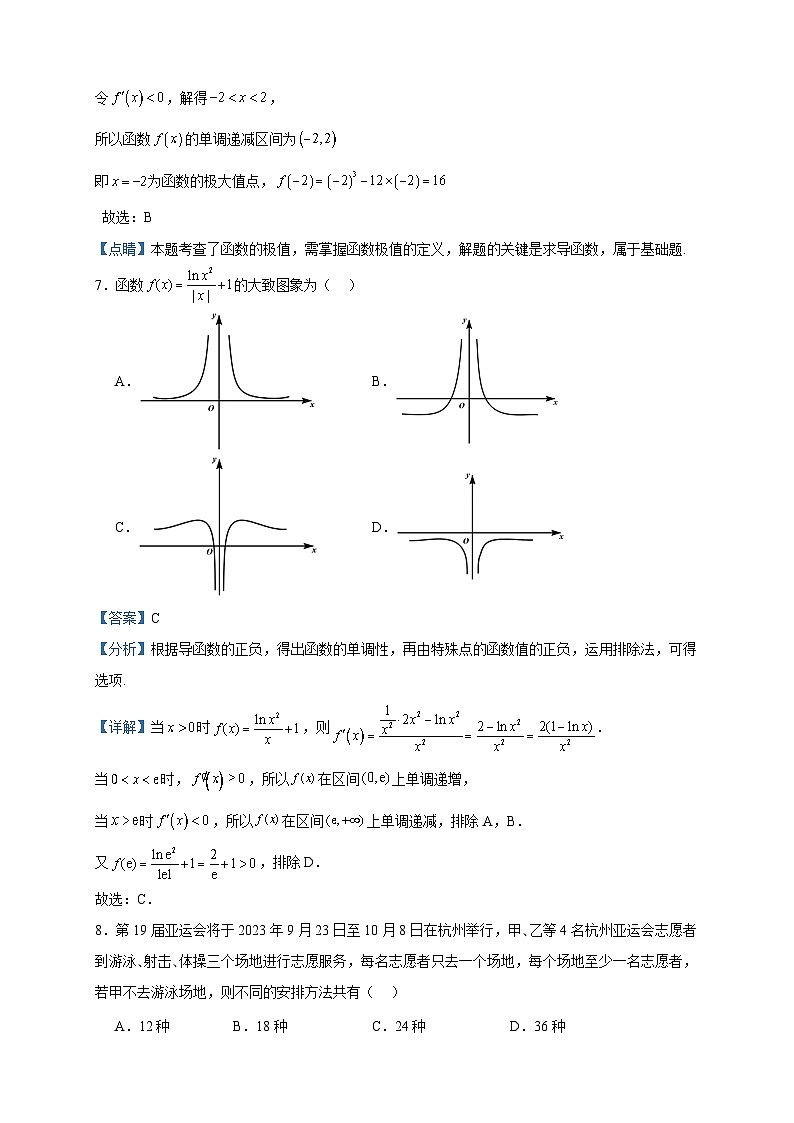
7．函数的大致图象为（    ）

A． B．

C． D．

【答案】C

【分析】根据导函数的正负，得出函数的单调性，再由特殊点的函数值的正负，运用排除法，可得选项.

【详解】当时，则．

当时，，所以在区间上单调递增，

当时，所以在区间上单调递减，排除A，B．

又，排除D．

故选：C．

8．第19届亚运会将于2023年9月23日至10月8日在杭州举行，甲､乙等4名杭州亚运会志愿者到游泳､射击､体操三个场地进行志愿服务，每名志愿者只去一个场地，每个场地至少一名志愿者，若甲不去游泳场地，则不同的安排方法共有（    ）

A．12种 B．18种 C．24种 D．36种

【答案】C

【分析】本题只需考虑游泳场有2名志愿者和1名志愿者两种情况即可.

【详解】①游泳场地安排2人，则不同的安排方法有种，

②游泳场地只安排1人，则不同的安排方法有种，

所以不同的安排方法有种.

故选：C

9．书包中装有大小相同的2本数学书和2本语文书，若每次从中随机取出一本书且不放回，则在第二次取出的是数学书的条件下，第一次取出的是语文书的概率为（    ）

A． B． C． D．

【答案】D

【分析】根据条件概率公式可求出结果.

【详解】设事件：第一次取出的是语文书，事件：第二次取出的是数学书，

则.

故选：D

10．若函数有两个极值点，且，则（    ）

A． B． C． D．

【答案】C

【分析】由极值点定义确定的关系，化简，由此求的范围.

【详解】因为函数有两个极值点，

又函数的定义域为，导函数为，

所以方程由两个不同的正根，且为其根，

所以，，，

所以，

则

，

又，即，可得，

所以或（舍去），

故选：C.

二、填空题

11．i是虚数单位，则复数      .

【答案】

【分析】根据复数代数形式的除法运算法则计算可得；

【详解】

故答案为：

12．若，则a4+a2+a0＝    

【答案】41

【分析】利用特殊值法，令x＝0，1，﹣1，将所得结果进行运算可得解．

【详解】令x＝0，可得a0＝1；

令x＝1，可得a0+a1+a2+a3+a4＝1，

即a1+a2+a3+a4＝0   ①；

令x＝﹣1，可得a0﹣a1+a2﹣a3+a4＝81，

即﹣a1+a2﹣a3+a4＝80  ②，

将①和②相加可得，2（a2+a4）＝80，

所以a2+a4＝40，

所以a0+a2+a4＝41．

故答案为41．

【点睛】本题考查二项式展开式的系数的求解方法：赋值法，对题目中的x合理赋值是解题的关键，属于基础题．

13．若，则      .

【答案】6

【分析】由求得，由此求得.

【详解】，即，

由题意可得，，解得且，

∴，解得．

∴．

故答案为：6．

14．一个盒子里装有大小相同的4个黑球，3个红球，2个白球，从中任取2个，其中红球的个数记为，则          

【答案】

【分析】先X的可能取值为：0，1，2，分别求出，直接求出数学期望即可.

【详解】红球的个数记为则，X的可能取值为：0，1，2，.

则；；.

所以.

故答案为：.

15．已知函数存在减区间，则实数a的取值范围为      .

【答案】

【分析】函数存在减区间，则有解可求解．

【详解】由题可知，

因为函数存在减区间，则在上有解，

即有解，

令，，

令，解得；令，解得，

所以在单调递减，单调递增，

所以，

因为有解，所以，

解得．

故答案为：

16．给图中A，B，C，D，E，F六个区域进行染色，每个区域只染一种颜色，且相邻的区域不同色.若有4种颜色可供选择，则共有   种不同的染色方案.

【答案】96

【分析】通过分析题目给出的图形，可知要完成给图中、、、、、六个区域进行染色，最少需要3种颜色，即同色，同色，同色，由排列知识可得该类染色方法的种数；也可以4种颜色全部用上，即，，三组中有一组不同色，同样利用排列组合知识求解该种染法的方法种数，最后利用分类加法求和．

【详解】解：要完成给图中、、、、、六个区域进行染色，染色方法可分两类，第一类是仅用三种颜色染色，

即同色，同色，同色，则从四种颜色中取三种颜色有种取法，三种颜色染三个区域有种染法，共种染法；

第二类是用四种颜色染色，即，，中有一组不同色，则有3种方案不同色或不同色或不同色），先从四种颜色中取两种染同色区有种染法，剩余两种染在不同色区有2种染法，共有种染法．

由分类加法原理得总的染色种数为种．

故答案为：96．

【点睛】本题考查了排列、组合、及简单的计数问题，解答的关键是正确分类，明确相邻的两区域不能染相同的颜色，属于中档题．

三、解答题

17．已知函数，.

(1)当时，求函数的极值；

(2)若对任意，不等式恒成立，求的取值范围.

【答案】(1)极大值为，无极小值

(2)

【分析】（1）求出函数的导函数，即可求出函数的单调区间，从而求出函数的极值；

（2）利用导数求出函数的最大值，依题意可得，解得即可.

【详解】（1）解：当时，，则，

令，得，令，得

∴函数在上单调递增，在上单调递减，

∴函数的极大值为，无极小值；

（2）解：

当，，则是增函数.

当时，则是减函数，

∴的最大值为，

∵恒成立，

∴，解得，

∴的取值范围为.

18．为弘扬体育精神，营造校园体育氛围，某校组织“青春杯”3V3篮球比赛，甲、乙两队进入决赛．规定：先累计胜两场者为冠军，一场比赛中犯规4次以上的球员在该场比赛结束后，将不能参加后面场次的比赛．在规则允许的情况下，甲队中球员都会参赛，他上场与不上场甲队一场比赛获胜的概率分别为和，且每场比赛中犯规4次以上的概率为．

(1)求甲队第二场比赛获胜的概率；

(2)用表示比赛结束时比赛场数，求的期望；

(3)已知球员在第一场比赛中犯规4次以上，求甲队比赛获胜的概率．

【答案】(1)

(2)

(3)

【分析】（1）设“第i场甲队获胜”，“球员第i场上场比赛”，，2，3．

根据对立事件的概率公式即可求解；

（2）由题意知的可能取值为2，3，结合对立事件和独立事件的概率公式和数学期望的计算公式即可求解；

（3）根据对立事件、独立事件的概率公式和条件概率公式计算即可求解.

【详解】（1）设“第i场甲队获胜”，“球员第i场上场比赛”，，2，3．

由全概率公式．

（2）的可能取值为2，3．

由题意知，由（1）知，

则，，

，

，．

（3），此时，

．

19．已知函数.

(1)求函数的单调区间;

(2)比较与的大小,并加以证明.

【答案】（1）在上单调递增，在上单调递减，在上单调递增.（2）

【详解】试题分析：（１）先求导数，再求导函数零点，列表分析导函数符号，对应确定单调区间，（２）构造差函数，求导得单调性，根据零点存在定理确定零点区间以及满足条件，根据单调性确定函数最小值取法，最后确定最小值大于零.

试题解析：解：（1），

令，得，；

令，得或；

令，得.

故在上单调递增，在上单调递减，在上单调递增.

（2）.

证明如下：

设 ，∵为增函数，

∴可设，∵，，∴.

当时，；当时，.

∴ ，

又，∴，

∴ .

∵，∴，

∴，.

点睛：利用导数证明不等式常见类型及解题策略(1) 构造差函数.根据差函数导函数符号，确定差函数单调性，利用单调性得不等量关系，进而证明不等式.（2）根据条件，寻找目标函数.一般思路为利用条件将求和问题转化为对应项之间大小关系，或利用放缩、等量代换将多元函数转化为一元函数.

20．已知函数，.

(1)讨论函数的单调性；

(2)若函数有两个零点，，且，曲线在这两个零点处的切线交于点，求证：小于和的等差中项；

(3)求证：，.

【答案】(1)答案见解析;

(2)证明见解析;

(3)证明见解析.

【分析】（1）求导，结合函数定义域为，分参数，来讨论导函数的符号即可；

（2）先根据导数的几何意义写出两条切线，联立切线得到的表达式，为证明题干只需证明，然后转化成双变量问题的不等式处理，接着通过换元：，把双变量问题转化成单变量问题解决；

（3）利用的结论进行辅助证明.

【详解】（1）的定义域为，

当时，，在上单调递减；

当时，令，又因为，可解得

单调递增，

单调递减；

（2）因为函数有两个零点,而单调函数至多只有一个零点，根据（1）可知.

 ， 所以曲线在和处的切线分别是：

.

联立两条切线解得：.

要证小于和的等差中项，即证，整理得：

由题意得

即证  

令，即证.

令.

所以在单调递减，所以

所以得证，故小于和的等差中项得证.

（3） ， ，

当 时， ， 时， ，

在x=0处取得最小值 ，知： 在上恒成立，

所以 ，当且仅当x=0时等号成立，

令 ， 代入上面不等式得： ，即 ，

；

综上，.

【点睛】关键点点睛: 关键点是令把二元函数变成一元函数，构造函数求导函数根据性质解题即可.