








































































新人教版高中数学选择性必修第三册全套教案word版带素养
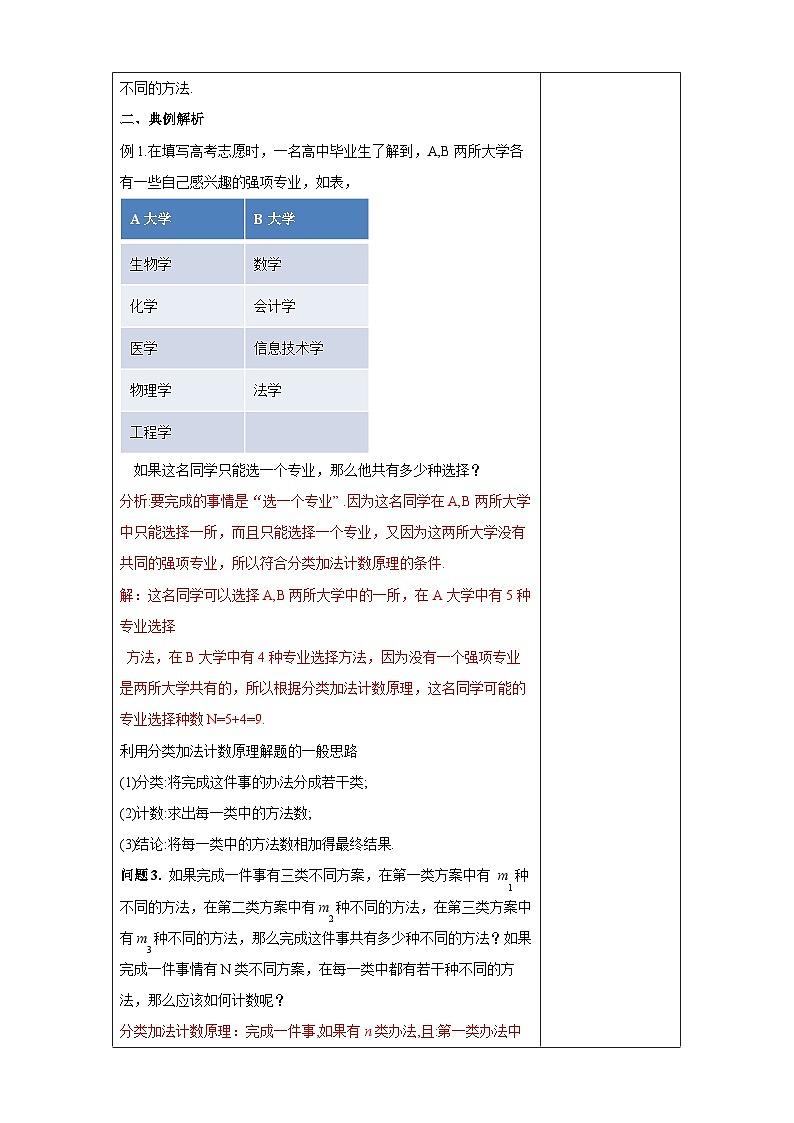
展开7.4.2超几何分布
本节课选自《2019人教A版高中数学选择性必修第三册》,第七章《随机变量及其分布列》,本节课主本节课主要学习超几何分布
超几何分布是一类应用广泛的概率模型,常常与二项分布问题综合运用,本节是学生已经学习了随机事件、等可能事件概率、互斥事件概率、条件概率和相互独立事件概率的求法、也学习了分布列的有关内容。它是对前面所学知识的综合应用。节课是从实际出发,通过抽象思维,建立数学模型,进而认知数学理论,应用于实际的过程。
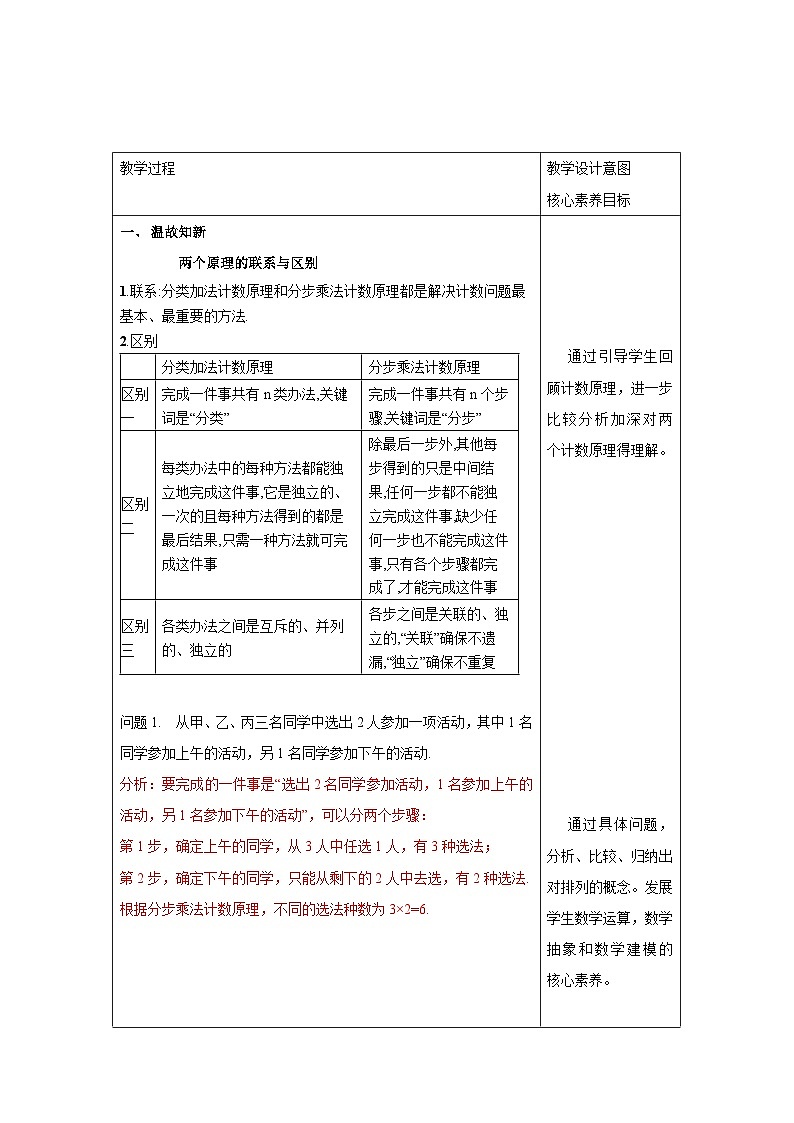
课程目标 | 学科素养 |
A. 理解超几何分布,能够判定随机变量是否服从超几何分布; B.能够利用随机变量服从超几何分布的知识解决实际问题,会求服从超几何分布的随机变量的均值. | 1.数学抽象:超几何分布的概念 2.逻辑推理: 超几何分布与二项分布的联系与区别 3.数学运算:超几何分布的有关计算 4.数学建模:模型化思想 |
重点:超几何分布的概念及应用
难点:超几何分布与二项分布的区别与联系
多媒体
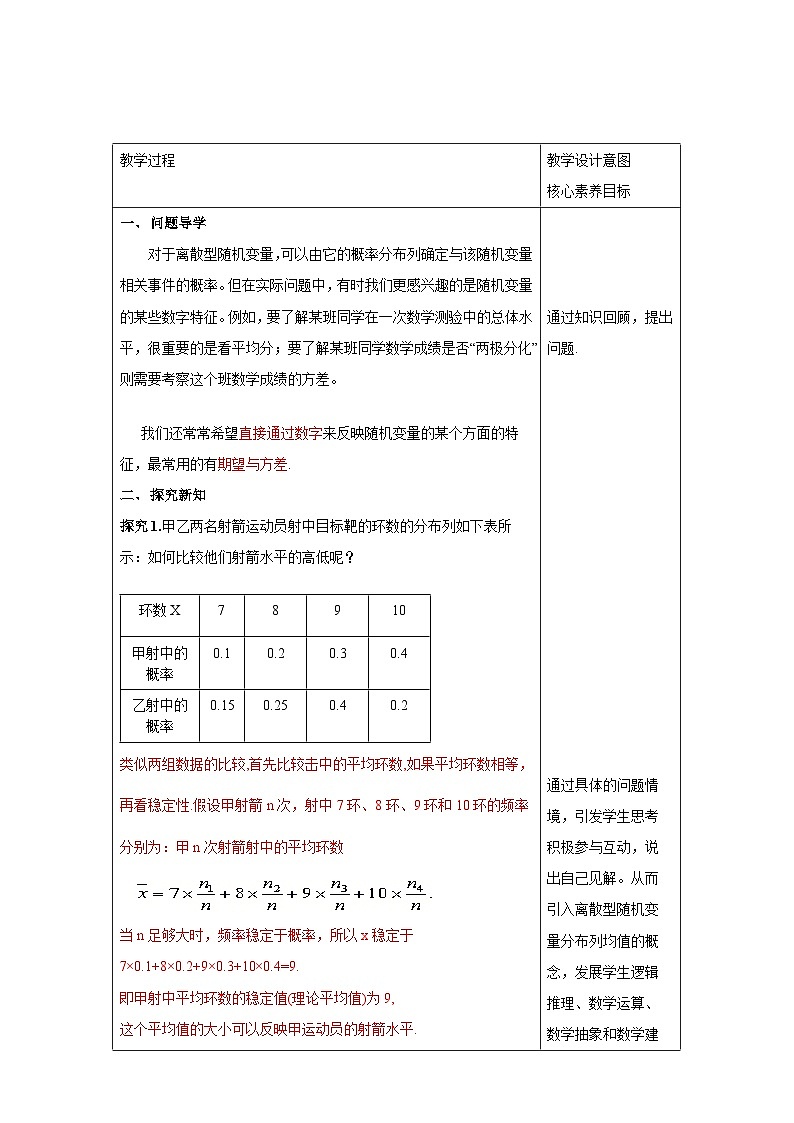
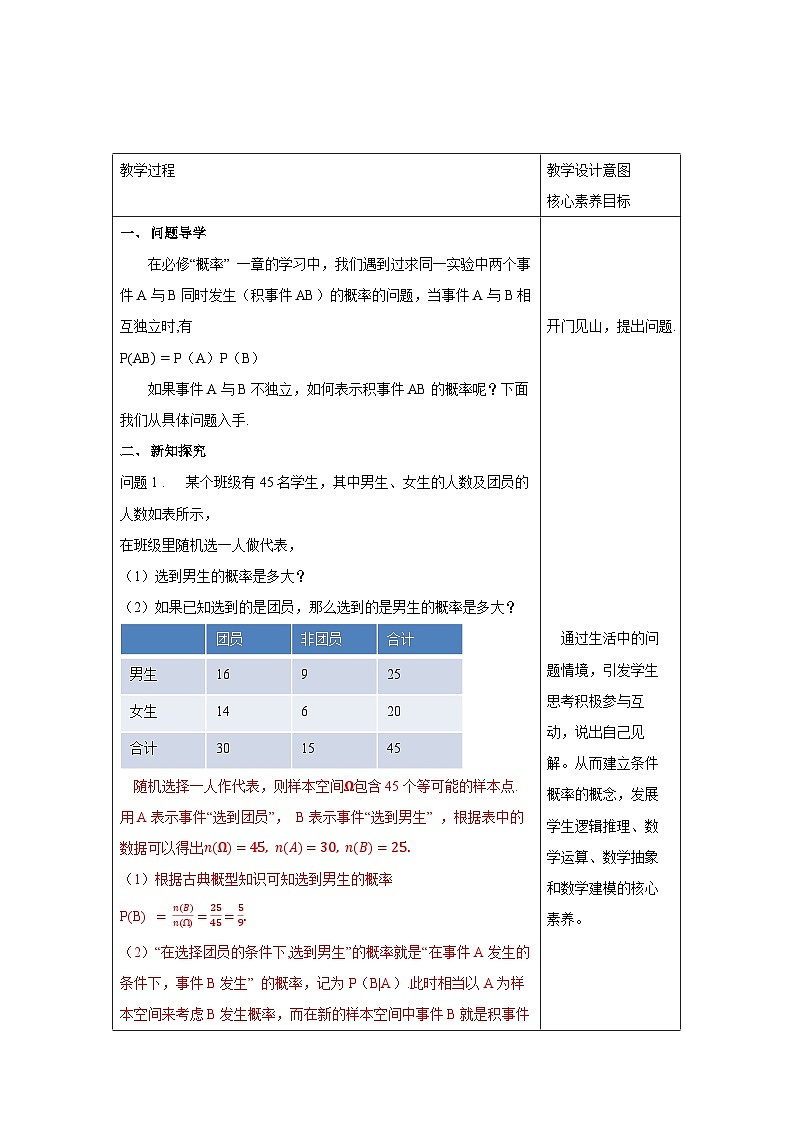
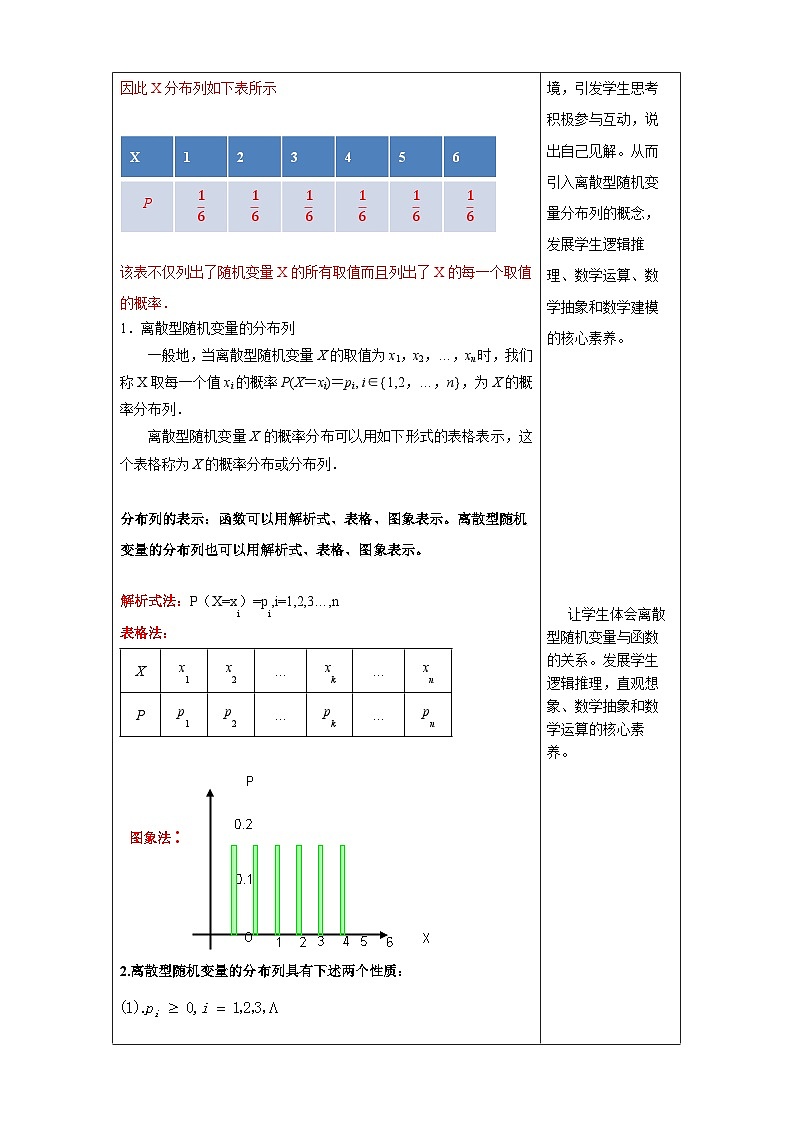
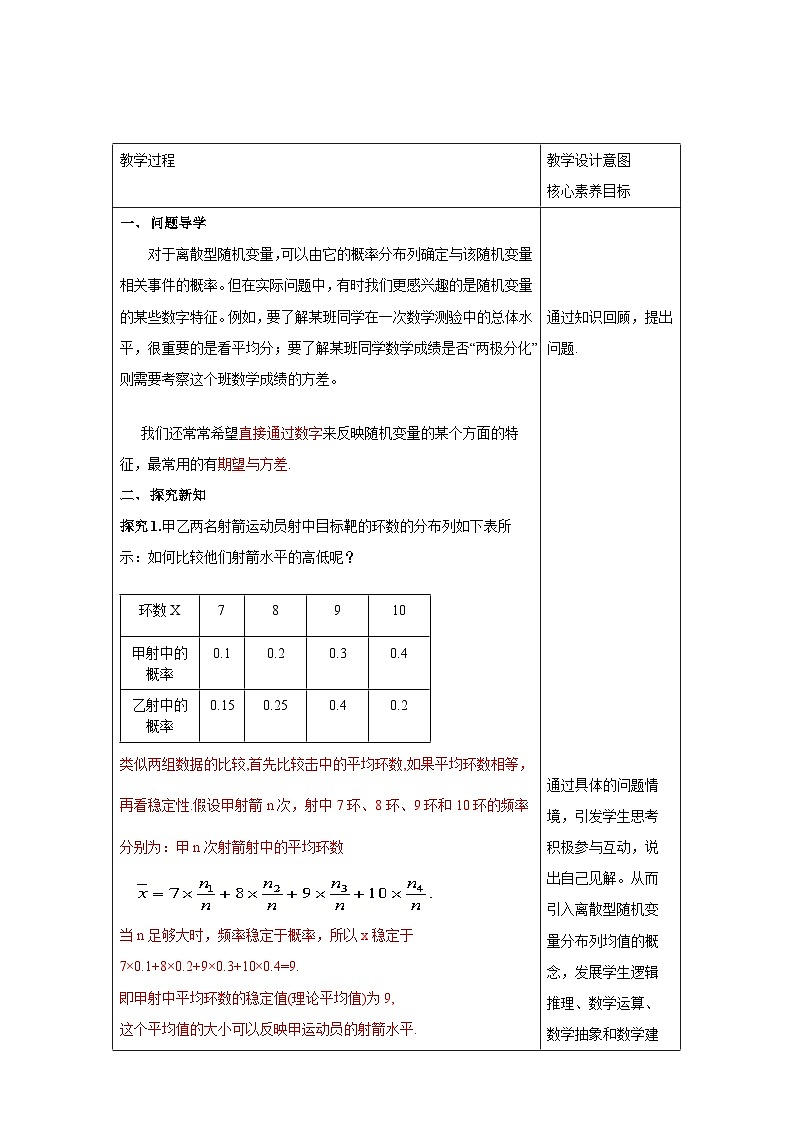
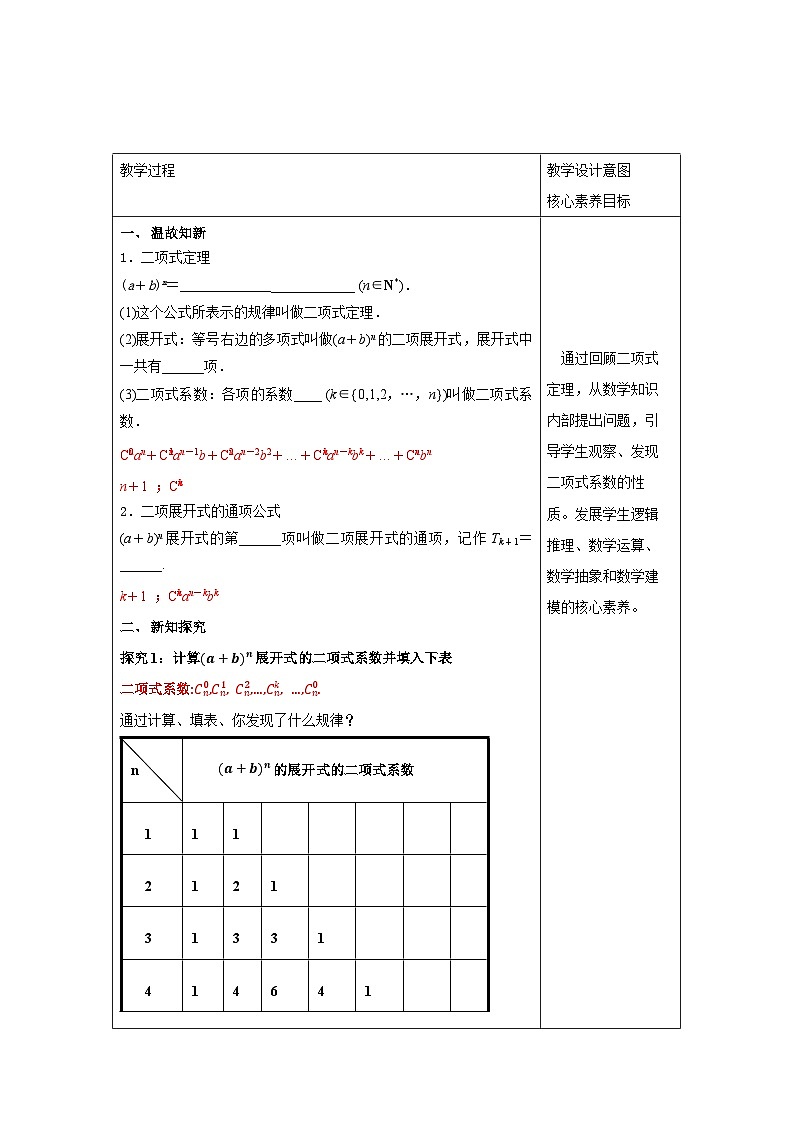
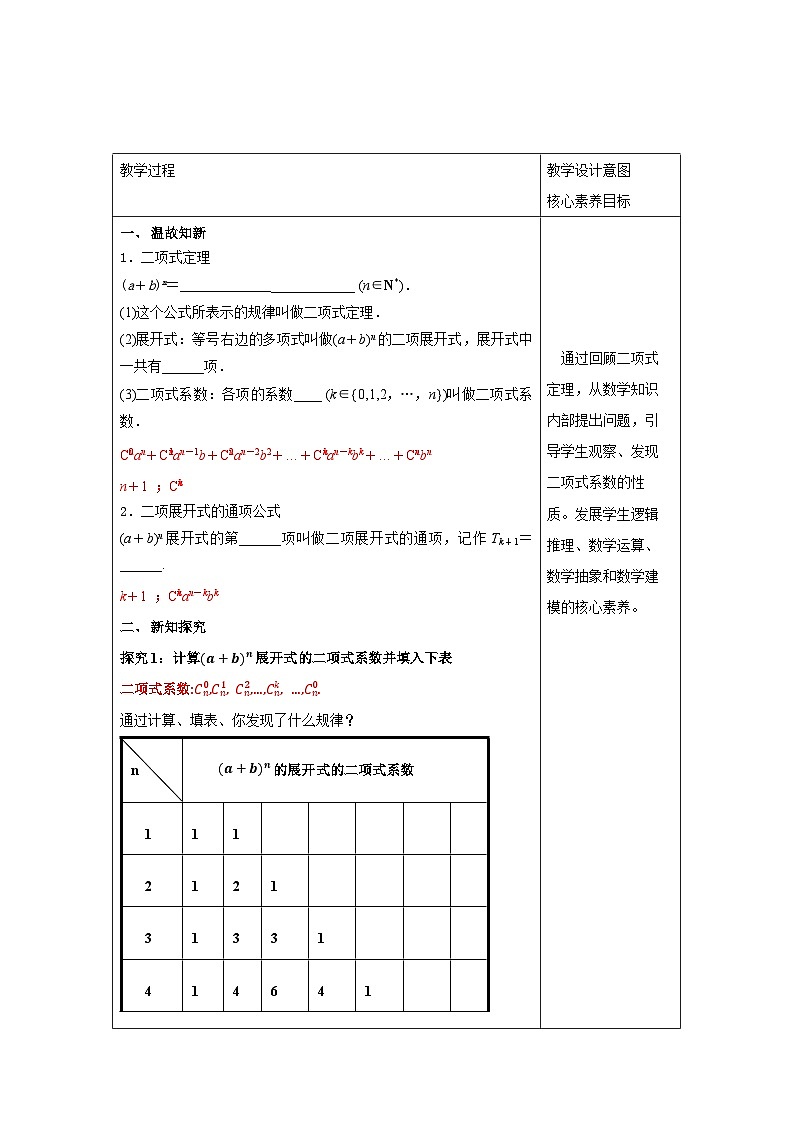
教学过程 | 教学设计意图 核心素养目标 | ||||||||||||||||||||||||
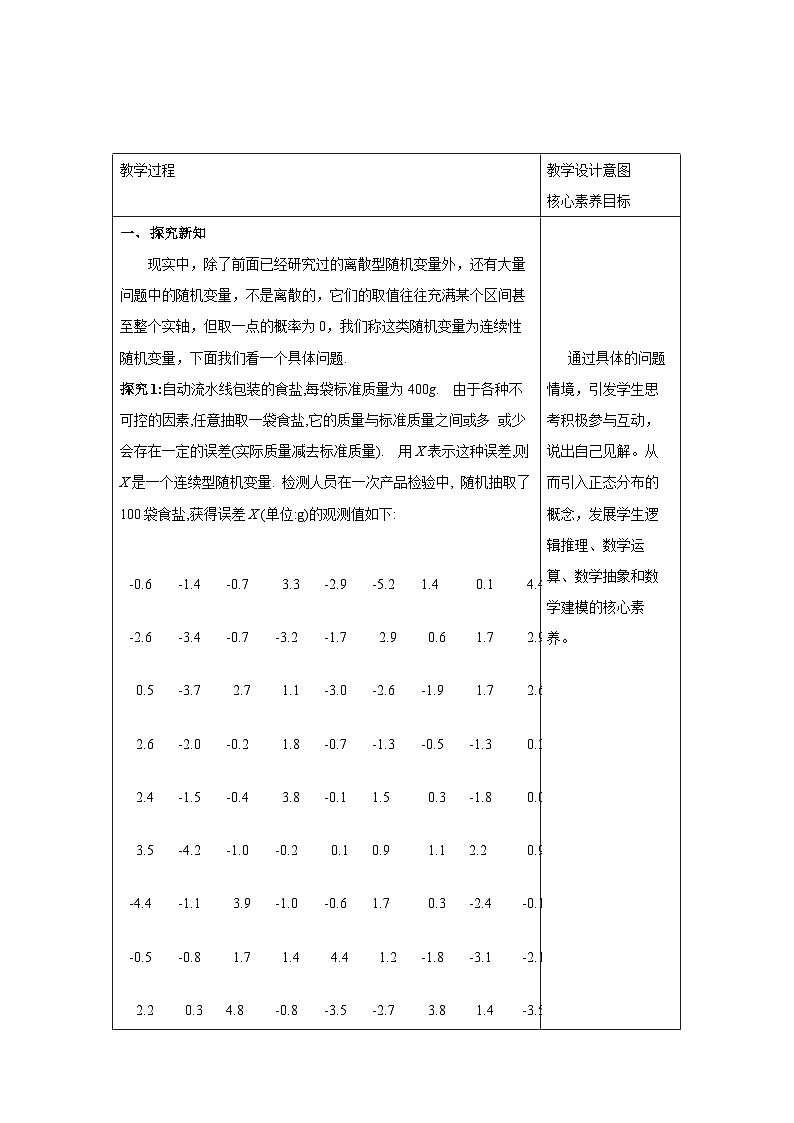
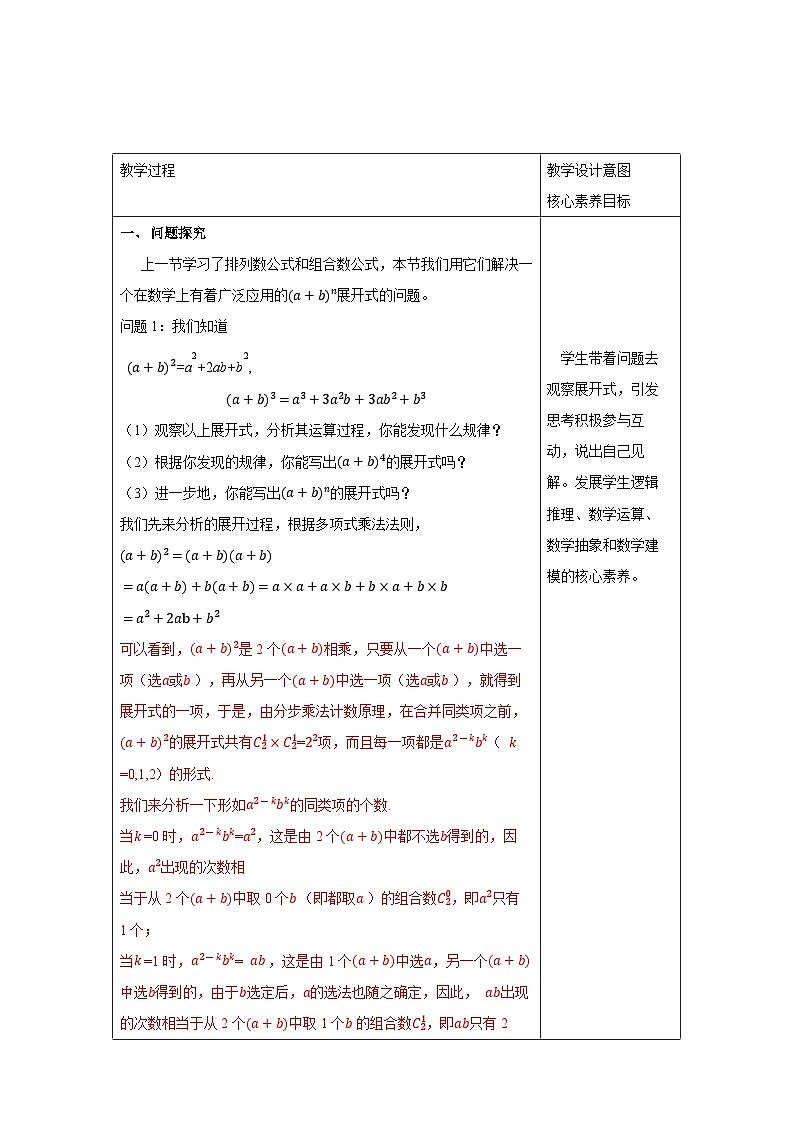
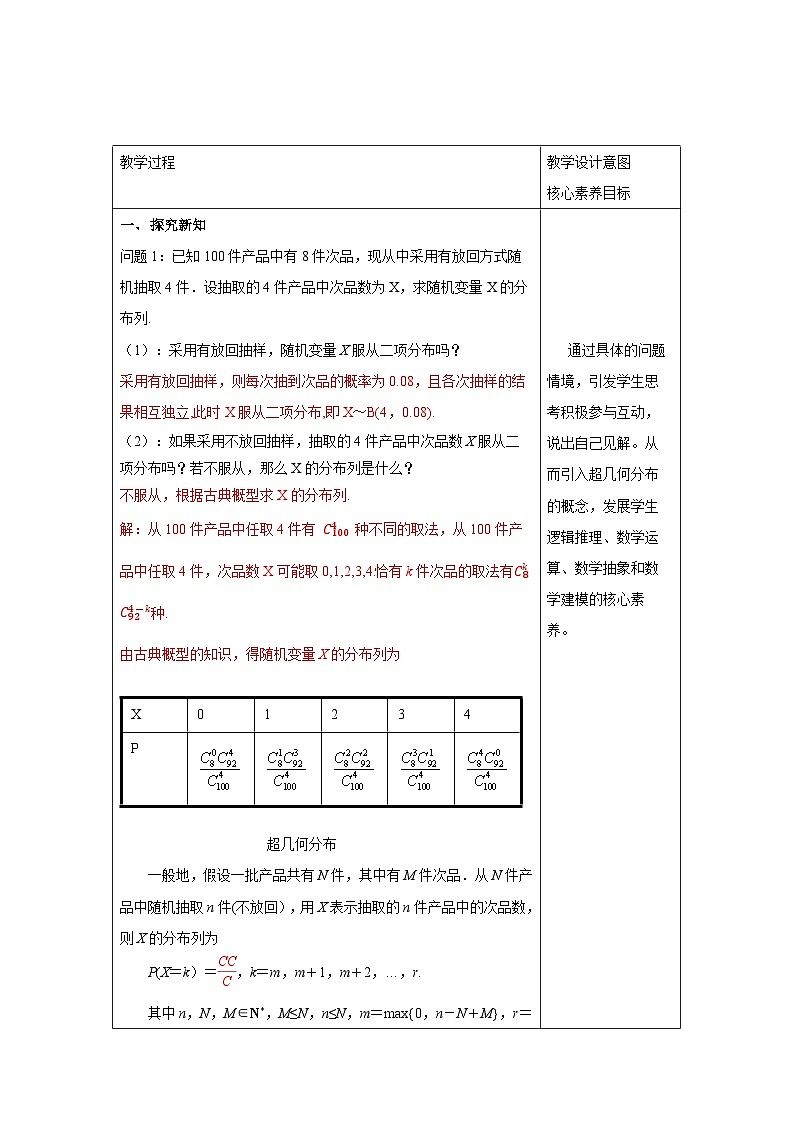
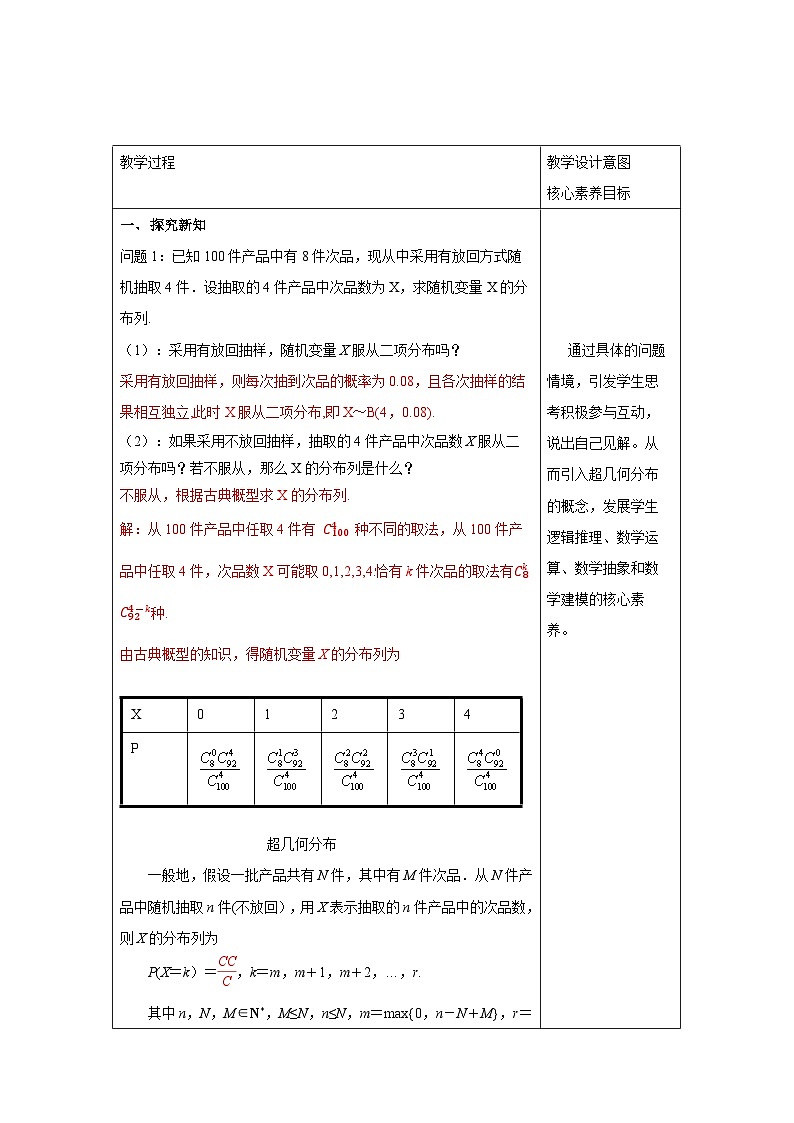
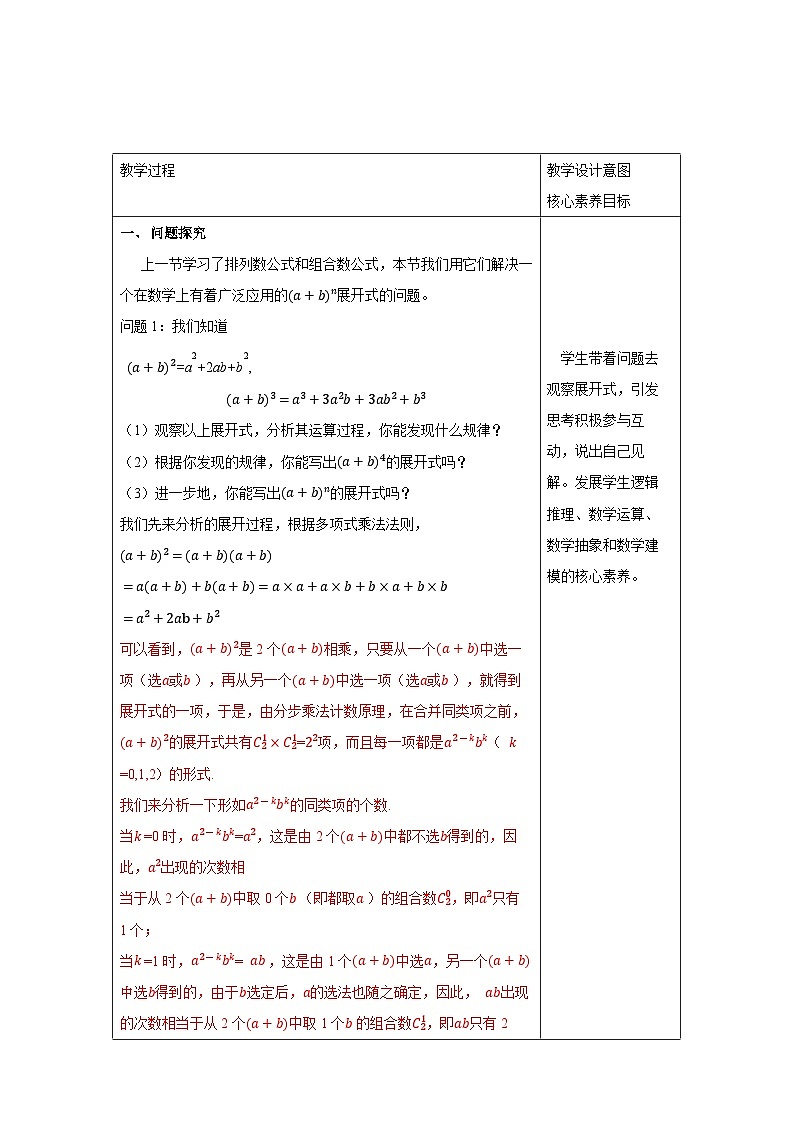
一、 探究新知 问题1:已知100件产品中有8件次品,现从中采用有放回方式随机抽取4件.设抽取的4件产品中次品数为X,求随机变量X的分布列. (1):采用有放回抽样,随机变量X服从二项分布吗? 采用有放回抽样,则每次抽到次品的概率为0.08,且各次抽样的结果相互独立,此时X服从二项分布,即X~B(4,0.08). (2):如果采用不放回抽样,抽取的4件产品中次品数X服从二项分布吗?若不服从,那么X的分布列是什么? 不服从,根据古典概型求X的分布列. 解:从100件产品中任取4件有 种不同的取法,从100件产品中任取4件,次品数X可能取0,1,2,3,4.恰有k件次品的取法有种. 由古典概型的知识,得随机变量X的分布列为
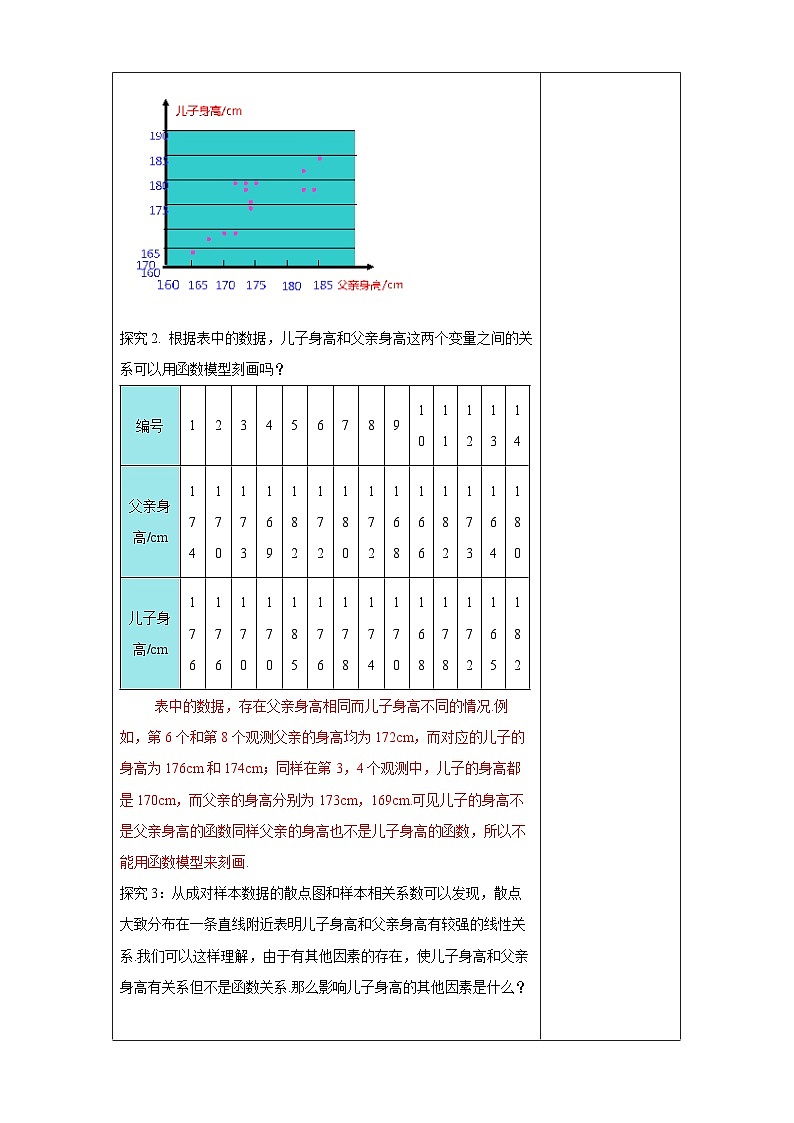
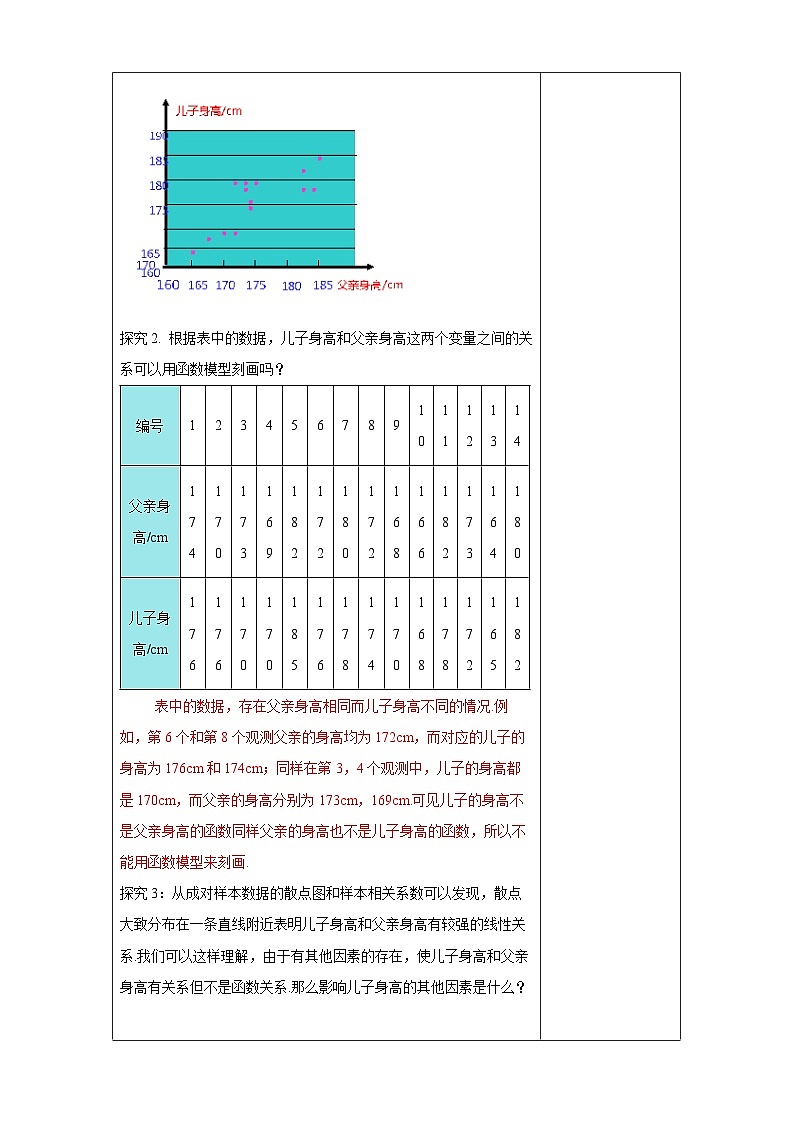
超几何分布 一般地,假设一批产品共有N件,其中有M件次品.从N件产品中随机抽取n件(不放回),用X表示抽取的n件产品中的次品数,则X的分布列为 P(X=k)=,k=m,m+1,m+2,…,r. 其中n,N,M∈N*,M≤N,n≤N,m=max{0,n-N+M},r=min{n,M},则称随机变量X服从超几何分布. 1.公式 中个字母的含义 N—总体中的个体总数 M—总体中的特殊个体总数(如次品总数) n—样本容量 k—样本中的特殊个体数(如次品数) 2.求分布列时可以直接利用组合数的意义列式计算,不必机械记忆这个概率分布列. 3. “任取n件,恰有k件次品”是一次性抽取,用组合数列式. 4.各对应的概率和必须为1. 1.下列随机事件中的随机变量X服从超几何分布的是( ) A.将一枚硬币连抛3次,正面向上的次数X B.从7名男生与3名女生共10名学生干部中选出5名优秀学生干部,选出女生的人数X C.某射手射击的命中率为0.8,现对目标射击1次,记命中目标的次数为X D.盒中有4个白球和3个黑球,每次从中摸出1个球且不放回,X是首次摸出黑球时的总次数 解析:由超几何分布的定义可知B正确. 答案:B 二、典例解析 例1:从50名学生中随机选出5名学生代表,求甲被选中的概率. 解: 设X表示选出的5名学生中含甲的人数(只能取0或1),则X服从超几何分布,且N=50,M=1,n=5.因此,甲被选中的概率为 例2. 一批零件共有30个,其中有3个不合格,随机抽取10个零件进行检测,求至少有1件不合格的概率. 解:设抽取的10个零件中不合格品数为?,则?服从超几何分布,且?=30,?=3,?=10, ?的分布列为, 至少有1件不合格的概率为?(?≥1)=?(?=1)+?(?=2)+?(?=3) 另解:(?≥1)=1−?(?=0) (1)当研究的事物涉及二维离散型随机变量(如:次品、两类颜色等问题)时的概率分布可视为一个超几何分布; (2)在超几何分布中,只要知道参数N,M,n就可以根据公式求出X取不同值时的概率. 跟踪训练1.在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用.现有6名男志愿者A1,A2,A3,A4,A5,A6和4名女志愿者B1,B2,B3,B4,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示. (1)求接受甲种心理暗示的志愿者中包含A1但不包含B1的概率; (2)用X表示接受乙种心理暗示的女志愿者人数,求X的分布列. 解析:(1)记“接受甲种心理暗示的志愿者中包含A1, 但不包含B1”的事件为M,则P(M)==. (2)由题意知X的所有可能取值为0,1,2,3,4,则 P(X=0)==,P(X=1)==, P(X=2)==,P(X=3)==, P(X=4)==. 因此X的分布列为
探究1:服从超几何分布的随机变量的均值是什么? 设随机变量X服从超几何分布,则X可以解释为从包含M件次品的N件产品中,不放回地随机抽取n件产品中的次品数.令p=,则p是N件产品的次品率,而 是抽取的n件产品的次品率, E()=p,即E(X)=np. 超几何分布的均值 设随机变量X服从超几何分布,则X可以解释为从包含M件次品的N件产品中,不放回地随机抽取n件产品中的次品数.令p=,则E(X)=__ np_. 例6.一袋中有100个大小相同的小球,其中有40个黄球,60个白球,从中随机摸出20个球作为样本.用X表示样本中黄球的个数. (1).分别就有放回和不放回摸球,求X的分布列; (2).分别就有放回和不放回摸球,用样本中黄球的比例估计总体中黄球的比例, 求误差不超过0.1的概率.
解:(1)对于有放回摸球,由题意知?~?(20,0.4),?的分布列为
对于不放回摸球,由题意知?服从超几何分布,?的分布列为 (2) 样本中黄球的比例 是一个随机变量 有放回摸球:P(||≤0.1)=P(6≤X≤10)≈0.7469; 不放回摸球:P(||≤0.1)=P(6≤X≤10)≈0.7988. 因此,在相同的误差限制下,采用不放回摸球估计的结果更可靠些。
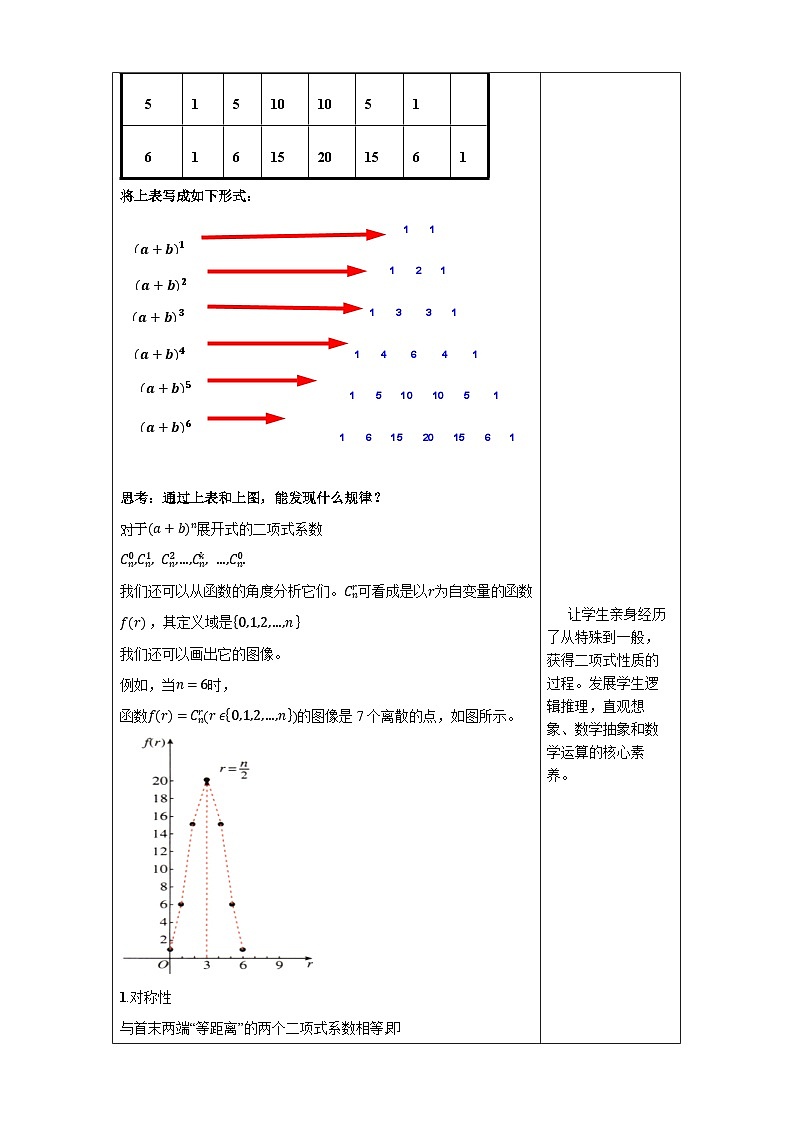
两种摸球方式下,随机变量X服从二项分布和超几何分布.这两种分布的均值相等都等于8. 但从两种分布的概率分布图看,超几何分布更集中在均值附近. 当n远远小于N时,每次抽取一次,对N的影响很小.此时,超几何分布可以用二项分布近似. 二项分布与超几何分布区别和联系 1.区别:一般地,超几何分布的模型是“取次品”是不放回抽样,而二项分布的模型是“独立重复试验”对于抽样,则是有放回抽样. 2.联系:当次品的数量充分大,且抽取的数量较小时,即便是不放回抽样,也可视其为二项分布.
|
通过具体的问题情境,引发学生思考积极参与互动,说出自己见解。从而引入超几何分布的概念,发展学生逻辑推理、数学运算、数学抽象和数学建模的核心素养。
通过问题分析,让学生掌握超几何分布的概念及其特点。发展学生逻辑推理,直观想象、数学抽象和数学运算的核心素养。
通过典例解析,在具体的问题情境中,深化对超几何分布的理解。发展学生逻辑推理,直观想象、数学抽象和数学运算的核心素养。
| ||||||||||||||||||||||||
三、达标检测 1.一袋中装5个球,编号为1,2,3,4,5,从袋中同时取出3个,以ξ表示取出的三个球中的最小号码,则随机变量ξ的分布列为( )
解析:随机变量ξ的可能值为1,2,3,P(ξ=1)==, P(ξ=2)==,P(ξ=3)==.故选C. 答案:C 2.已知100件产品中有10件次品,从中任取3件,则任意取出的3件产品中次品数的数学期望为________. 解析:次品数服从超几何分布,则E(X)=3×=0.3. 答案:0.3 3. 在高二年级的联欢会上设计了一个摸奖游戏,在一个口袋中装有5个红球和10个白球,这些球除颜色外完全相同,一次从中摸出3个球,至少摸到2个红球就中奖,求中奖的概率. 解析:由题意知,摸到红球个数X为离散型随机变量,X服从超几何分布,则至少摸到2个红球的概率为 P(X≥2)=P(X=2)+P(X=3) =+=. 故中奖的概率为. 4.在10件产品中有2件次品,连续抽3次,每次抽1件,求: (1)不放回抽样时,抽取次品数ξ的均值; (2)放回抽样时,抽取次品数η的均值. 解析:(1)方法一 P(ξ=0)==; P(ξ=1)==;P(ξ=2)==, ∴随机变量ξ的分布列为
E(ξ)=0×+1×+2×=. 方法二 由题意知P(ξ=k)=(k=0,1,2), ∴随机变量ξ服从超几何分布,n=3,M=2,N=10, ∴E(ξ)===. (2)由题意,知每次取到次品的概率为=, ∴η~B, ∴E(η)=3×=. |
通过练习巩固本节所学知识,通过学生解决问题,发展学生的数学运算、逻辑推理、直观想象、数学建模的核心素养。
| ||||||||||||||||||||||||
二、 小结 1.超几何分布 2.超几何分布的均值 五、课时练 |
通过总结,让学生进一步巩固本节所学内容,提高概括能力。 |
课后通过对教学过程的反思与研究, 才能不断完善教学设计中的不足, 才能提升教材分析的能力和课堂教学实效.
1. 多元展示, 多方评价. 在教学过程中我借问题牵引,保证了课堂教学的顺利实施;而在整个过程中,我对学生所作练习、疑问及时解析评价;学生之间、小组之间的互相评价补充,使学生共享成果分享喜悦,坚定了学好数学的信念,实现了预期目标.
2. 创造性的使用教材. 有别于教材,我在教学中,让学生考察了分别考察了两类题型之后再引导学生进行归纳, 这样更贴近学生的认知水平, 学生课后反馈,效果较为理想.
新人教版高中数学五本书全套系列选择性必修第一册: 这是一份人教A版 (2019)选择性必修 第一册全册综合教学设计及反思,共634页。
新人教版高中数学五本书全套系列选择性必修第三册: 这是一份人教A版 (2019)全册综合教学设计,共532页。
新人教版高中数学五本书全套系列选择性必修第二册: 这是一份高中全册综合教学设计及反思,共356页。













