






高教版(2021·十四五)基础模块 上册1.1 集合及其表示评课ppt课件
展开这是一份高教版(2021·十四五)基础模块 上册1.1 集合及其表示评课ppt课件,共26页。PPT课件主要包含了集合的概念,集合的表示法等内容,欢迎下载使用。
图书馆专区内所有数学书可以组成一个集合.
中国古代四大发明可以组成一个集合.
平面上到原点O的距离等于1的所有点可以组成一个集合.
1.1.1 集合的概念
一般地,由某些确定的对象组成的整体称为集合,简称为集.组成这个集合的对象称为这个集合的元素.
集合常用大写英文字母表示.如,A,B,C,….;集合的元素常用小写英文字母表示.如,a,b,c,….
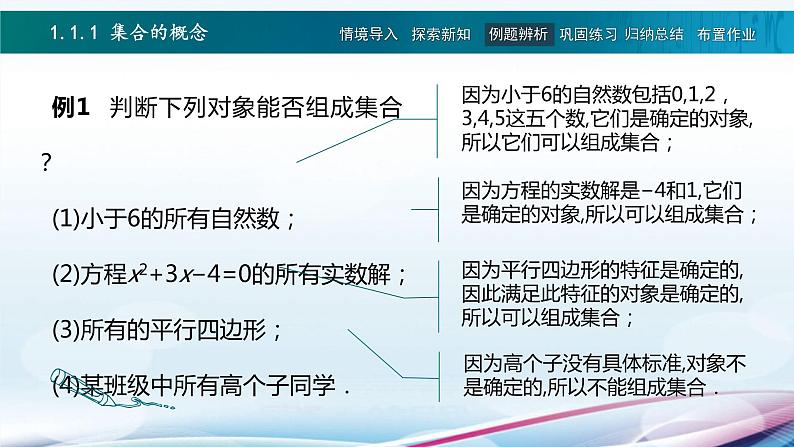
例1 判断下列对象能否组成集合?(1)小于6的所有自然数;(2)方程x2+3x−4=0的所有实数解;(3)所有的平行四边形;(4)某班级中所有高个子同学.
如果a是集合A的元素,就说a属于A,记作a∈A, 读作“a属于A”.如果a不是集合A的元素,就说a不属于A,记作a∉A,读作“a不属于A”.
组成集合的对象必须是确定的;同一个集合中的元素必须是互不相同的.
例2 方程x2=4的所有实数解组成的集合为A,则-2_____A,5_____A(用符号“∈ ”或“∉”填空).
解 因为(-2)²=4,所以-2是方程 x ²=4的解,故-2∈A .因为5 ²≠4, 所以5不是方程 x ²=4的解,故5∉ A .
1.下列各语句中的对象能否组成集合?如果能组成集合,写出它的元素.如果不能组成集合, 请说明理由.
(1)某校汉字录入速度快的学生;(2)某校汉字录入速度为90字符/min及以上的所有学生;(3)方程(2x-3)(x+1)=0的所有实数解;(4)大于-5且小于5的整数;(5)大于3且小于1的所有实数;(6)非常接近0的数.
2.用符号“∈”或“∉”填空.
3.判断下列集合是有限集还是无限集. (1)你所在班级的所有同学组成的集合; (2)方程 x+2=0的所有正整数解组成的集合; (3)小于3的所有整数组成的集合; (4)数轴上表示大于0且小于1的所有点组成的集合.
1.1.2 集合的表示法
小于6的正整数组成一个集合, 大于3的实数也组成一个集合.那么, 除了用这种自然语言表示集合, 还可以如何表示集合呢?
1.列举法:把集合的所有元素一一列举出来,中间用逗号隔开,再用花括号“{ }”把它们括起来,这种表示集合的方法称为列举法.
例3 用列举法表示下列集合. (1)中国古典长篇小说四大名著组成的集合; (2) 大于-3且小于10的所有偶数组成的集合.
解 (1)中国古典长篇小说四大名著组成的集合用列举法表示为{《水浒传》,《三国演义》,《西游记》,《红楼梦》}
(2)大于-3且小于10的所有偶数为-2,0,2,4,6,8它们组成的集合用列举法表示为{-2,0,2,4,6,8}.
2.描述法:利用元素的特征性质来表示集合的方法称为描述法.描述法表示集合时,在花括号“{ }”中画一条竖线,竖线的左侧是集合的代表元素及取值范围,竖线的右侧是元素所具有的特征性质.
例4 用描述法表示下列集合:(1)小于1的所有整数组成的集合 ;(2)所有偶数组成的集合(3)在平面直角坐标系中,由第一象限内的所有点组成的集合
{x| x=2k, x∈Z},也可以表示为{偶数}
{(x,y) | x>0,y>0}
例5 用写出不等式2x+1>9的解集.
解 由不等式2x+1>9 , 得 2x>8 , 故 x>4 .因此不等式 2x+1>9的解集可以用描述法表示为{x|x>4} .
例6 分别用列举法和描述法表示方程x²-9=0的解集.
解 解方程x²-9=0,得x1=-3, x2=3.故方程的解组成的集合用列举法表示为 {-3,3} ,
用描述法表示为 {x|x=-3或 x=3} .
有些集合只能用列举法或描述法表示,有些集合两种方法都适用,要根据需要具体问题进行具体分析.
1. 用列举法表示下列集合:(1)大于-5且小于9的所有奇数组成的集合;(2)方程x²-2x-3=0的解集.
2. 用描述法表示下列集合. (1)大于-1且小于3 的所有实数组成的集合; (2)平方等于9的所有实数组成的集合.
1.书面作业:完成课后习题和学习与训练;2.查漏补缺:根据个人情况对课题学习复习与回顾;3.拓展作业:阅读教材扩展延伸内容.
相关课件
这是一份数学基础模块上册1.1 集合及其表示教学课件ppt,共25页。PPT课件主要包含了集合的概念,集合的表示法等内容,欢迎下载使用。
这是一份中职数学第1章 集合1.1 集合及其表示背景图ppt课件,共16页。PPT课件主要包含了测测你们的文化底蕴,中国四大名著,东北三省,对象是明确的,例题1,例题2,确定性,互异性,无序性,整数以及分数等内容,欢迎下载使用。
这是一份高中数学高教版(中职)基础模块上册(2021)1.1.2 集合的表示法授课课件ppt,共17页。PPT课件主要包含了学习目标,温馨提示,课堂小结,作业布置等内容,欢迎下载使用。












