人教版七年级上册第四章 几何图形初步4.2 直线、射线、线段授课ppt课件

这是一份人教版七年级上册第四章 几何图形初步4.2 直线、射线、线段授课ppt课件，共36页。PPT课件主要包含了课前导入，新课精讲，学以致用，课堂小结，情景导入，探索新知，典题精讲，小试牛刀，同学们下节课见等内容，欢迎下载使用。
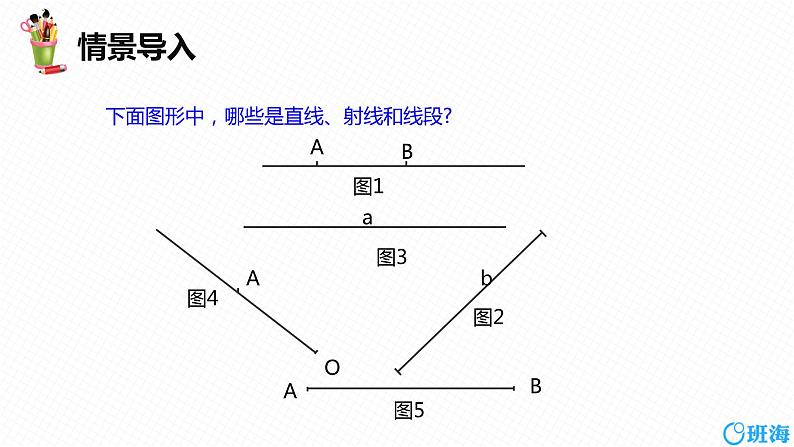
下面图形中，哪些是直线、射线和线段?
尺规作图：在数学中，我们常限定用无刻度的直尺和圆规作图，这就是尺规作图，利用尺规作图可以将一条线段移到另一条线段上．用直尺(无刻度)和圆规作一条线段等于已知线段的步骤：(1)利用直尺(无刻度)作一条射线AB；(2)用圆规量出已知线段的长度a(测量时使圆规两只脚的顶点分别与线 段两端点重合，则圆规两只脚的顶点之间的距离即为线段的长度)；
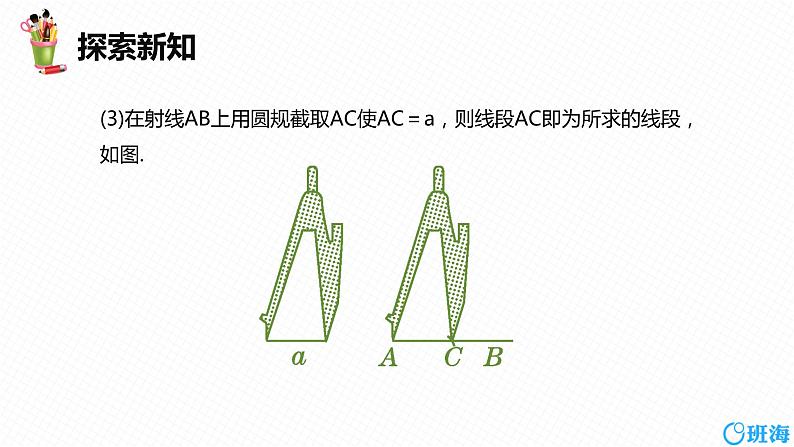
(3)在射线AB上用圆规截取AC使AC＝a，则线段AC即为所求的线段，如图.
例1 已知线段a，b，如图①，画线段AC＝a＋b.导引：通过尺规作图把两条线段转移到同一条直线上，连接在一起即可． 解：步骤1：画直线AD； 步骤2：在直线AD上依次截取AB＝a，BC＝b， 则线段AC＝a＋b，如图②.
作线段的和及倍数问题，一般都在所作直线上依次截取；作线段的差在被减数的线段内也依次截取，余下的线段即为所求线段的差．
1.尺规作图的工具是(　　) A．刻度尺和圆规 B．三角尺和圆规 C．直尺和圆规 D．没有刻度的直尺和圆规
2.如图，已知线段a，b，作线段AB，使AB＝2a－b(注明作图步骤)．
解：如图，(1)作射线AE；(2)在射线AE上顺次截取AC＝CD＝a；(3)在线段AD上截取DB＝b，则线段AB即为所求作的线段．
线段AB和线段CD哪一条长?
思考 请同学们思考并回答下面的问题：(1) 怎样比较两个同学的高矮? (2) 怎样比较两根筷子的长短?
比较两根筷子的长短的方法：
① 一头对齐，两根棒靠紧， 观察另一头的位置；
注意：在几何里更多的用前面所说的方法进行比较.
② 用刻度尺分别度量出筷子的长度.
同一长度单位下，数量大的较长.
线段长短的比较方法：(1)度量法，用刻度尺分别量出两条线段的长度再比较；(2)叠合法，使两条线段的一个端点重合，另一个端点在同一侧，从而比较出两条线段的长短．
例2 如图所示，是一张三角形纸片，你能比较线段AB与线段BC的长短吗？导引：可以利用度量法，分别量出每条线段的长度，然后进行比较，或者利用叠合法进行比较． 解：把边BC折到AB上，使AB与BC重合，可知点C在线段AB上，所以AB＞BC.
比较两条线段的长短可以用叠合法或度量法，如果使用叠合法，就设法将两线段一端端点重合，另外两个端点放在公共端点的同侧，再观察另外两个端点的位置关系；如果使用度量法，则分别度量出两条线段的长，然后比较度量值的大小．
1.下列图形中能比较大小的是(　　) A．两条线段 B．两条直线 C．直线与射线 D．两条射线2.比较线段a和b的大小，其结果一定是(　　) A．a＝b B．a＞b C．a＜b D．a＞b或a＝b或a＜b
3.为了比较线段AB与CD的大小，小明将点A与点C重合使两条线段在一 条直线上，结果点B在CD的延长线上，则(　　) A．AB＜CD B．AB＞CD C．AB＝CD D．以上都不对
若点M把线段AB分成相等的两条线段AM和BM， 则点M叫线段AB的中点.
2.对线段的中点的认识： (1)线段的中点是线段上的点，且把线段分成相等的两条线段； (2)一条线段的中点有且只有一个； (3)如图，若M是AB的中点，则①AM＝BM＝ AB；②AB＝2AM＝2BM；③AM＋BM＝AB且AM＝BM.反过来也成立．
例3 如图，M是线段AB的中点，N是线段AM上一点，则下列结论不一定成立的是(　　)A．MN＝BM－AN　　　　 B．MN＝ AB－ANC．MN＝ AM D．MN＝BN－AM导引：由图知MN＝AM－AN，由线段中点定义知AM＝BM＝ AB，所以A，B正确；又由图知MN＝BN－BM，易知D正确．
解答有关线段之间关系的题，一般要根据题中给定的条件，结合图中已有条件进行解答，如本例我们是根据线段中点定义得出的线段关系，结合图中MN与其他线段关系来进行解答的．
例4 画线段MN＝3 cm，在线段MN上取一点Q，使MQ＝NQ；延长线段MN到点A，使AN＝ MN；延长线段NM到点B，使BM＝ BN. 计算：(1)线段BM的长；(2)线段AN的长．导引：首先根据题意画出图形，再从图形中寻找数量关系进行计算．
解：如图. (1)因为MN＝3 cm，MQ＝NQ，所以MQ＝NQ＝1.5 cm. 又因为BM＝ BN，所以MN＝ BN，即BN＝ MN＝4.5 cm. 所以BM＝BN－MN＝1.5 cm. (2)因为AN＝ MN，MN＝3 cm， 所以AN＝1.5 cm.
1.点C在线段AB上，下列条件中不能确定点C是线段AB中点的是(　　) A．AC＝BC B．AC＋BC＝AB C．AB＝2AC D．BC＝ AB2.下列说法正确的是(　　) A．若AC＝ AB，则C是AB的中点 B．若AB＝2CB，则C是AB的中点 C．若AC＝BC，则C是AB的中点 D．若AC＝BC＝ AB，则C是AB的中点
3.如图，C是线段AB上的一点，M是线段AC的中点，若AB＝8 cm，BC＝2 cm，则MC的长是(　　) A．2 cm B．3 cm C．4 cm D．6 cm
1．为了比较线段AB与CD的大小，小明将点A与点C重合使两条线段 在一条直线上，结果点B在CD的延长线上，则（ ) A．ABCD C．AB=CD D．无法确定哪条长
2．如图，AB=CD，则AC与BD的大小关系是（ )  A．AC>BD B．ACBC .
7．如图所示，在一条笔直公路a的两侧，分别有A，B两个村庄，现要在公路a上建一个汽车站C，使汽车站到A，B两村的距离之和最小，问汽车站C的位置应如何确定？ 
2.线段的两种比较方法：叠合法和度量法.
3.线段的中点的概念及表示方法.