初中沪科版1.6 有理数的乘方备课ppt课件

这是一份初中沪科版1.6 有理数的乘方备课ppt课件，共22页。PPT课件主要包含了学习目标，本节要点，学习流程，课时导入，知识点，乘方的意义，感悟新知，乘方的运算法则，5原式，本节小结等内容，欢迎下载使用。

乘方的意义乘方的运算法则
1.看下面的故事：从前，有个“聪明的乞丐”他要到了一块面包。他想，天天要饭太辛苦，如果我第一天吃这块面包的一半，第二天再吃剩余面包的一半，……依次每天都吃前一天剩余面包的一半，这样下去，我就永远不用去要饭了！请你们交流讨论，再算一算，如果把整块面包看成整体“1”，那第十天他将吃到面包的______.
2.拉面馆的师傅用一根很粗的面条，把两头捏合在一起拉伸，再捏合，再拉伸，反复多次，就能把这根很粗的面条，拉成许多很细的面条.想想看，捏合　　　次后，就可以拉出32根面条.
1.乘方 ：求n个相同因数的积的运算，叫做乘方，乘方的结果叫做幂，如： ，记作an，读作a的n次方，其中a叫做底数，n叫做a的幂的指数，简称指数，当an看作a的n次方的结果时，也可读作“a的n次幂”．如：
2. 乘方的意义 a n 表示n 个相同因数a 的积，其中相同的因数是底数，因数的个数是指数，因此，可以把相同因数的乘法转化为乘方或把乘方转化为乘法.
特别提醒1. 有理数的乘方可以看作是一种特殊的乘法运算.2. 乘方具有双重意义，它不仅表示一种运算——求几个相同因数的积的运算，还表示这种运算的结果——幂.
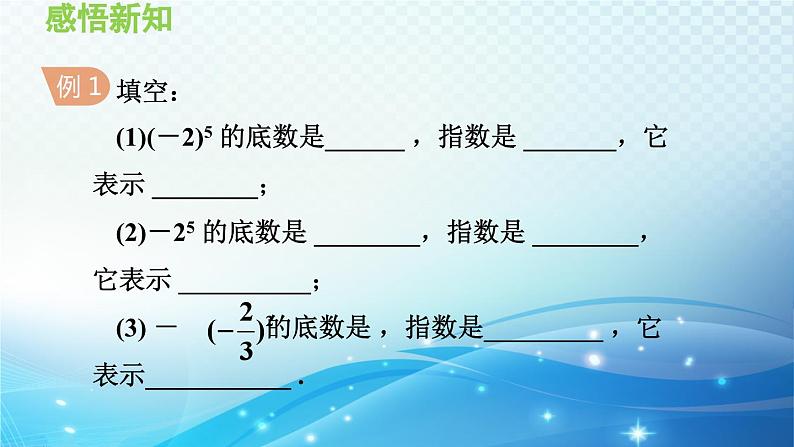
填空：(1)(－2)5 的底数是______ ，指数是 _______，它表示 ________；(2)－25 的底数是 ________，指数是 ________，它表示 __________；(3) － 的底数是 ，指数是_________ ，它表示___________ .
误区警示当底数是分数或负数时，要用括号将底数括起来，若没有括号，则底数就改变了.一个数可以看作这个数本身的一次方，例如4 就是41，m就是m1，指数1通常省略不写.
解题秘方：利用乘方的意义确定底数、指数.
解：(1)(－2)5 的底数是－2，指数是5，它表示(－2)×(－2)×(－2)×(－2)×(－2)；(2)－25 的底数是2，指数是5，它表示－2×2×2×2×2；(3) 的底数是 ，指数是2，它表示 × .
答案：(1)－2；5；(－2)×(－2)×(－2)×(－2)×(－2)(2)2；5；－2×2×2×2×2 (3)
1. 有理数的乘方运算法则(1)正数的任何次乘方都取正号；(2)负数的奇次乘方取负号，负数的偶次乘方取正号；(3)0 的任何正整数次幂都是0.
特别解读有理数的乘方运算法则主要揭示幂的符号法则.一看底数，二看指数，确定符号后还是按照有理数的乘法算出其结果.
2. 有理数的乘方运算计算一个有理数的乘方时，应将乘方运算转化为乘法运算，先确定幂的符号，再计算幂的绝对值. 特别地，当底数较大时，可借助于计算器计算.3. 用计算器计算乘方不同类型的计算器操作方法可能有所不同，用计算器计算时，要弄清计算器中每个键的作用，结合有理数运算的顺序，进行计算.
计算：(1)(－5)4； (2)－54；
(5)(－1)2 022；
解题秘方：先确定幂的符号，再转化为乘法运算算出结果.
特别解读1. 若两个数互为相反数，则它们的奇次幂(指数相同)互为相反数，偶次幂(指数相同)相等.2. －1 的奇次幂等于－1，－1 的偶次幂等于1. 3. 当求带分数的乘方时，要先把带分数化成假分数，然后分子、分母分别乘方.
解：：(1)原式=(－5)×(－5)×(－5)×(－5)=625.(2)原式=－(5×5×5×5)=－625.
方法总结：an，－an 及(－a)n 的区别与联系：
有理数的乘方运算主要是将它转化为有理数的乘法运算来进行计算的，因此它具有如下性质：(1)负数的奇次幂是负数，负数的偶次幂是正数；(2)正数的任何次幂都是正数，0的任何正整数次幂都是0.