还剩7页未读，继续阅读

下载需要10学贝 1学贝=0.1元

使用下载券免费下载

加入资料篮

立即下载

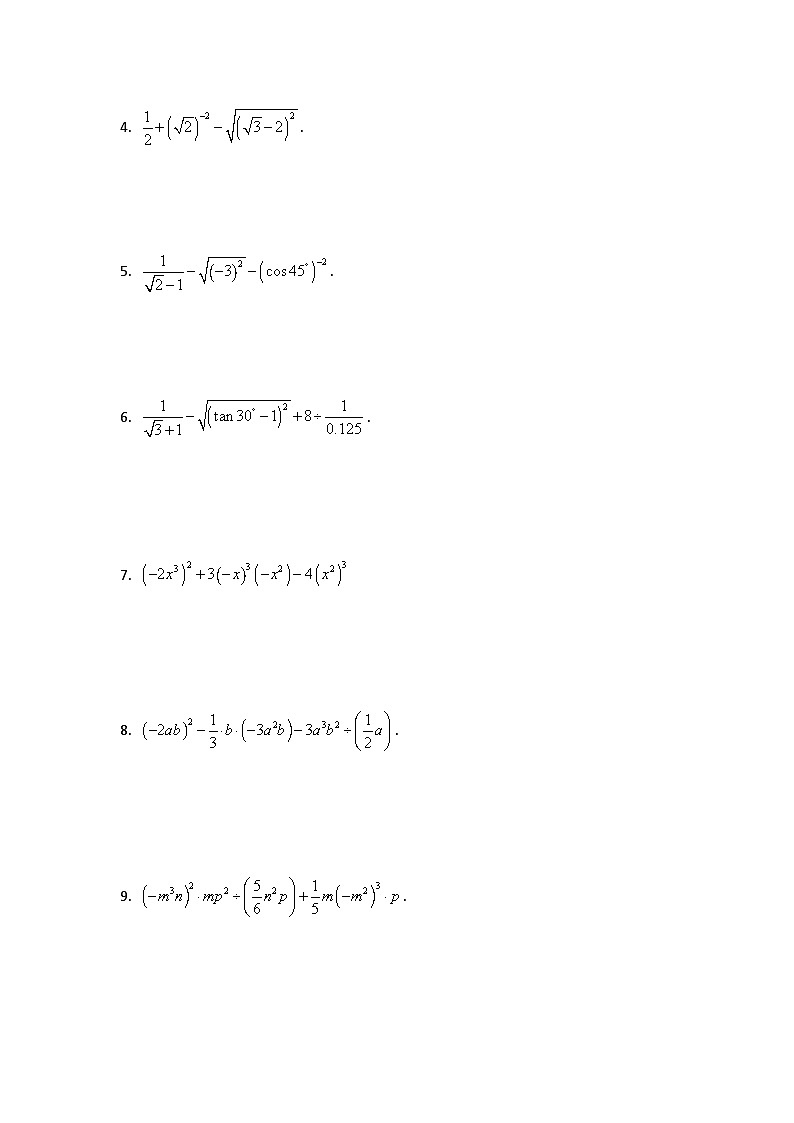
所属成套资源：2024年中考数学专题复习

成套系列资料，整套一键下载

浏览整套资料 (共5份)

2024年中考数学专题复习——专题一计算

展开

这是一份2024年中考数学专题复习——专题一计算，共10页。

2024年中考数学专题复习

专题一计算

第01讲基本运算

课前预习

1. 回顾三角函数的相关概念，借助直角三角形（图1，图2）填写下表。


正弦
余弦
正切

（备注：，，）

图1

图2

2. 填空.

（1）若分式有意义，则的取值范围为 .

（2）已知，则的取值范围为 .

（3）若不等式的解集为，则的取值范围为 .

（4）如图，在中，，，，则 .

3. 解方程并回答下列问题： .

使方程左右两边相等的末知数的值叫做方程的；对于分式方程而言，如果化简后的整式方程的解恰好使得原分式方程的分母为零，那么这个解叫做分式方程的，所以解分式方程的最后一个环节是检验.

知识精讲

实数运算

数与式整式运算

分式运算→消元

方程组（多元） →消元

一元二次方程（高次）→降次

→整式方程→一元一次方程

→验根

→消元/降次→一元一次不等式

→数形结合

1. 基本运算的操作规程

看结构，分部分；依法则，不跳步；警异常，巧检验.

检验原则： .

2. 解方程的依据是；解多元方程组的基本思路是；解高次方程的基本思路是 .分式方程先转化为，结果必须。

3. 解不等式的依据是；解不等式组的基本思路是转化为；求解集时，常借助找公共部分.

4. 方程（组）、不等式（组）有时也会用思想求解。

精讲精练

一、计算下列各题.

1. .

2. .

3. .

4. .

5. .

6. .

8. .

9. .

10.

二、化简求值

11. 先化简，然后从的范围内选取一个合适的整数作为的值代入求值.

12. 已知为一元二次方程的实数根，求代数式的值.

三、解下列方程（组）

13. .

14.

15. .

16. .

17.

18.

四、解不等式（组）

19. 已知，，求的取值范围.

20. 已知，，求的取值范围.

21. 已知，求的取值范围.

22. 已知，求的取值范围.

23. 已知且，求的取值范围及的最大值.

24. 已知，且为整数，当为何值时，最大？最大值为多少？

第02讲综合运算

知识精讲

一、综合运算问题的处理思路

1. 分析问题，明确目标；

2. 观察结构，分析特征；

3. 边运算，边调整.

注：

显性条件：正整数、负整数、无解、增根等。

隐性条件：由定义、性质、指代不明等造成的范围限制。

如：中；中；不等式的解集为，隐含，且与相等；解一元二次方程使用时，要保证二次项系数不为0。

二、变换思考角度是处理综合运算问题的常用手段

如：既可以看做一元二次方程，也可以看做一次函数。

精讲精练

1. 若，为实数，且满足，则 .

2. 若关于的分式方程有非负实数解，则的取值范围是 .

3. （1）已知关于的不等式的解集是，求关于的不等式的解集.

（2）已知，，求的取值范围.

4. 已知关于的方程（为实数）.

（1）求证：无论为何值，该方程总有解.

（2）若方程有两个不相等的实数根，求的取值范围.

（3）若为整数，且方程的两个实数根均为正整数，求的值.

（4）是否存在实数，使得方程的两个实数根互为相反数？如果存在，求出的值；如果不存在，请说明理由.

5. （1）若，，且，则 .

（2）已知，，且，则 .

6. 函数的自变量的取值范围是 .

7. 若方程有增根，则它的增根 .

8. 已知关于的方程的解也是不等式组的一个解，则的取值范围是 .

9. 若为实数，且满足，则 .

10. 已知关于的不等式的解集是，求的解集.

11. 已知，（为任意实数），则，的大小关系为（）

D.不能确定

12. 已知，若，则的取值范围是（）

13. 若关于的不等式组恰有三个整数解，则一次函数的图象与反比例函数的图象的交点有个.

14. 设关于的方程有两个不相等的实数根，，且，那么的取值范围是（）

15. 已知，为实数，则当时，最小，此时 .

16. 已知，，且，则 .

17. 已知实数，，满足，，，则的最小值为 .