2024年中考数学专题复习——专题四 动态几何

2024年中考数学专题复习

专题四  动态几何

第01讲  动点问题

课前预习

按要求完成下列题目：

如图1，直线和轴，轴的交点分别为点，点，点的坐标是.动点以每秒3个单位长度的速度从点出发沿方向运动，同时动点以每秒1个单位长度的速度从点出发沿线段向点运动. 当其中一个动点到达终点时，它们都停止运动. 设点运动秒时，的面积为.求出与的函数关系式.

要求：

（1）研究背景图形，将信息标注到图形上，发现为        三角形.

（2）补全运动过程分析图（图2），确定起点、终点及各个分段.

（3）根据运动过程，画出各段对应图形情况.

（4）借助，三角形相似表达相关线段长，并求出与之间的函数关系式.

图2

图3（备用）         

知识精讲

一、动点问题的处理思路

1. 研究背景图形.

2. 分析运动过程，画线段图，分段，定范围。（关注四要素）

（1）根据起点、终点，确定运动路径；

（2）速度（注意速度是否变化），借助s=ut确定时间（范围）；

（3）状态转折点，确定分段，常见状态转折点为拐点；

（4）所求目标——明确思考方向。

3.表达，分析几何特征，设计方案求解。

画出符合题意的图形，表达线段长，根据几何特征列方程求解，结合范围验证结果。

精讲精练

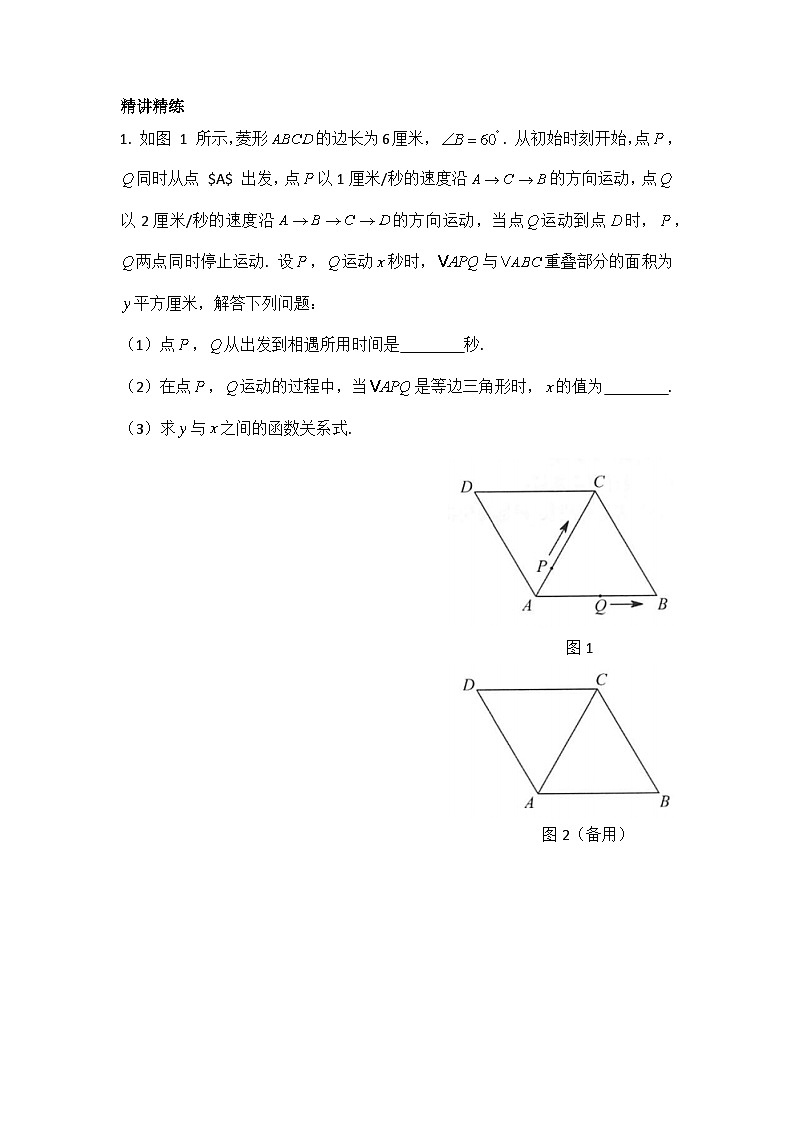
1. 如图 1 所示，菱形的边长为6厘米，. 从初始时刻开始，点，同时从点 $A$ 出发，点以1厘米/秒的速度沿的方向运动，点以2厘米/秒的速度沿的方向运动，当点运动到点时，，两点同时停止运动. 设，运动秒时，与重叠部分的面积为平方厘米，解答下列问题：

（1）点，从出发到相遇所用时间是        秒.

（2）在点，运动的过程中，当是等边三角形时，的值为        .

（3）求与之间的函数关系式.

图1         

图2（备用）    

2. 如图1，在边长为2的正方形中，是延长线上一点，且，动点从出发，以每秒1个单位长度的速度沿着的路线向点匀速运动（不与，重合），设运动时间为秒. 连接并延长交射线于.

（1）当为何值时，是等腰三角形？

（2）设四边形的面积为，请写出与之间的函数关系式.

（3）当点在边上时（不与，重合），若，交的平分线于点，当点恰好落在边上时，求此时的长.

图1             

图2（备用）       

图3（备用）      

图4（备用）     

3. 如图1，正方形中，点，的坐标分别为，，点在第一象限. 动点在正方形的边上，从点出发沿匀速运动，同时动点以相同的速度在轴正半轴上运动，当点到达点时，两点同时停止运动，设运动的时间为秒.

（1）当点在边上运动时，点的横坐标（长度单位）关于运动时间（秒）的函数图象如图2所示，请求出点开始运动时的坐标及点的运动速度.

（2）求正方形的边长及顶点的坐标.

（3）在（1）中当为何值时，的面积最大？并求出此时点的坐标.

（4）如果点，保持原速度不变，当点沿匀速运动时，与能否相等？若能，请求出所有符合条件的值；若不能，请说明理由.

图1        

图2        

图3（备用）  

图4（备用）  

图5（备用）  

4. 如图1，在中，，，，，，分别是，，的中点.点从点出发，沿折线以每秒7个单位长度的速度匀速运动；点从点出发，沿方向以每秒4个单位长度的速度匀速运动. 过点作射线，交折线于点. 点，同时出发，当点绕行一周回到点时，，两点都停止运动，设点，运动的时间是秒（）.

（1），两点间的距离是        .

（2）射线能否把四边形分成面积相等的两部分？若能，求出相应的值；若不能，说明理由.

（3）当点运动到折线上，且点又恰好落在射线上时，求的值.

（4）连接，当时，请直接写出的值.

图1             

图2（备用）        

图3（备用）        

图4（备用）        

图5（备用）        

第02讲  图形运动产生的面积问题

课前预习

按要求解决下列问题：

如图，正方形的边长为，在等腰中，，，且点，，，都在直线上.从点 $G$ 与点 $B$ 重合的位置开始，以的速度沿直线按图中箭头所示的方向做匀速直线运动，到点与点重合时停止运动. 设移动时间为（），与正方形重叠部分的面积为（），尝试画出运动状态分析图，并求出当时，关于的函数关系式.

要求：

（1）画运动通道，找碰撞点，计算碰撞时的值.

碰撞点 碰撞时的值

（2）根据上述碰撞点对应的碰撞时刻，画出运动状态分析图.

（3）画出对应图象.

（4）求出当时，关于的函数关系式.

知识精讲

1. 研究背景图形。

2. 分析运动过程，画线段图，分段，定范围。（需关注四要素）

（1）根据起始位置、终止位置、速度，确定的范围；

（2）状态转折点——确定分段，状态转折通常是边与顶点碰撞的时刻；

（3）所求目标——明确方向。

3. 分段画图，表达，分析形成因素，求解验证。

精讲精练

1. 如图 1，在平行四边形中，，，.以为斜边，在平行四边形的内部作，其中，.

（1）求的周长；

（2）若以每秒2个单位长度的速度沿向右平行移动，得到，当与重合时停止移动.设移动时间为秒，与重叠部分的面积为，请求出与之间的函数关系式，并写出的取值范围.

图1              

图2（备用）        

图3（备用）        

2. 已知，在矩形中，为边上一点，，，，为线段上一点，，连接. 如图1，现有一张硬质纸片，，，，斜边与边在同一直线上，点与点重合，点在线段上.如图2，从图1的位置出发，以每秒1个单位长度的速度沿向点匀速移动，同时点从点出发，以每秒1个单位长度的速度沿向点匀速移动，点为直线与线段的交点，连接. 当点到达终点时，和点同时停止运动. 设运动时间为秒，解答下列问题：

（1）在整个运动过程中，当点在线段上时，求的值.

（2）在整个运动过程中，是否存在点，使是等腰三角形？若存在，求出的值；若不存在，请说明理由.

（3）在整个运动过程中，设与重叠部分的面积为.请直接写出与之间的函数关系式以及自变量的取值范围.

图1           

图2           

图3（备用）      

图4（备用）        

图5（备用）        

3. 如图 1，在中，，，，点，同时从点出发，以的速度分别沿，匀速运动，当点到达点时，，两点同时停止运动. 过点作的垂线交于点，连接，，并作关于直线对称的图形，得到.设点的运动时间为（），与重叠部分的面积为（）.

（1）当为何值时，点恰好落在上？

（2）求与之间的函数关系式，并写出的取值范围.

图1         

图2（备用）     

图3（备用）    

4. 如图 1，在中，，，，动点从点出发，沿方向以的速度向点运动，动点从点同时出发，沿方向以的速度向点运动. 当点到达点时，，两点同时停止运动. 以为边向上作正方形，过点作，交于点. 设点的运动时间为（），正方形和梯形重叠部分的面积为（）.

（1）当        时，点与点重合；

（2）当        时，点在上；

（3）当点在，两点之间（不包括，两点）时，求与之间的函数关系式.

图1      

图2（备用）

图3（备用） 

图4（备用） 

图5（备用） 

第03讲  动态几何综合

知识点精

动态几何问题，是在动态背景下，探究图形性质和图形间关系的问题。动态背景主要涉及图形运动（点、线、形）及图形变换（平移、旋转、对称），常考查面积、存在性问题等。

解决此类问题，通常需要分析运动过程、分段画图，进而将整个运动过程拆分为几段逐一解决。

精讲精练

1. 如图, 四边形为矩形, , 射线 过点 且与 轴平行, 点分别是 和 轴正半轴 上的动点, 且满足 .

(1)①点 的坐标是        ；

②        ；

③当点 与点 重合时, 点 的坐标为        ；

(2) 设的中点为与线段相交于点 , 是否存 在点 , 使 为等腰三角形? 若存在, 请求出点 的横 坐标; 若不存在, 请说明理由.

(3) 设点 的横坐标为 与矩形重叠部分的 面积为 , 试求 与 之间的函数关系式和相应的自变量 的取值范围.

2. 如图, 在 Rt 中, , 点分别是边的中点, 连接. 动 点分别从点同时出发, 运动速度均为 , 点 沿 的方向运动到点 停止: 点 沿方向运动, 当点 停止运动时, 点 也随之停止运动. 在运动过程中, 过点 作的垂线交于点 , 以为顶点作 . 设 与矩形重叠部分的面积为 (这里规定线段是面积为 0 的几何图形), 点 的运 动时间为 .

(1) 当点 运动到点 时,         .

(2) 在点 从点 运动到点 的过程中, 某一时刻, 点 恰好落在上, 求此时的长度.

(3) 当点 在线段 $F D$ 上运动时, 求 与 之间的函数关系式.

3. 如图, 在矩形中, , 点 是的中 点, 点 在的延长线上, 且 , 一动点 从点 出发, 以每秒 1 个单位长度的速度沿匀速运动, 到达点 后, 立即以原速度沿返回; 另一动点 从点 出发, 以每秒 1 个単位长度的速度沿射线匀速运动, 点同时出发, 当两点相遇时停止运动. 在点的运动过程中, 以为 边作等边 , 使 和矩形在射线的同侧, 设运动的时间为 秒 .

(1) 当等边 的边恰好经过点 时, 求运动时间 的值.

(2) 在整个运动过程中, 设等边 和矩形重叠部分的面积为 , 请求出 与 之间的函数关系式及相应的自 变量 的取值范围.

(3) 设与矩形的对角线的交点为 , 是否存 在这样的 , 使 是等腰三角形? 若存在, 求出相应的 值; 若不存在, 请说明理由.

4. 如图, 在 Rt 中, , 点 在边上, 且 . 点同时从点 出发, 分别沿以每秒 1 个单位长度的速度向点匀速运动, 点 到达 点 后立刻以原速度沿向点 运动, 当点 运动到点 时, 点同时停止运动. 在点运动的过程中, 以为边作正方形, 使它与 在线段的同侧. 设运动的时间为 秒 , 正方形与 重 叠部分的面积为 , 求 与 之间的函数关系式.