【同步讲义】（人教A版2019）高中数学必修二：第九章 统计单元测试（强化卷）

第九章 统计单元测试强化卷

一、单选题

1．学校开展学生对食堂满意度的调查活动，已知该校高一年级有学生550人，高二年级有学生500人，高三年级有学生450人.现从全校学生中用分层抽样的方法抽取60人进行调查，则抽取的高二年级学生人数为（    ）

A．18 B．20 C．22 D．30

【答案】B

【分析】求出高一年级学生、高二年级学生、高三年级学生人数比，再列式计算作答.

【详解】依题意，该校高一年级学生、高二年级学生、高三年级学生人数比为：，

所以抽取的高二年级学生人数为.

故选：B

2．某沙漠地区经过治理，生态系统得到很大改善，野生动物数量有所增加．为调查该地区某种野生动物的数量，将其分成面积相近的150个地块，从这些地块中用简单随机抽样的方法抽取15个作为样区，调查得到样本数据，其中和分别表示第个样区的植物覆盖面积（单位：公顷）和这种野生动物的数量，经统计得，，则该地区这种野生动物数量的估计值（这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数）（    ）

A．60 B．1200 C．12000 D．6000

【答案】C

【分析】先计算15个样区的野生动物的平均数，然后再乘以地块数计算即可.

【详解】由题可知：15个样区的野生动物的平均数为

所以该地区这种野生动物数量的估计值为

故选：C

3．为了解某班学生每周购买零食的支出情况，利用分层随机抽样的方法抽取了15人进行调查，调查结果如下表，则估算全班学生每周购买零食的支出的方差是（    ）

A．10.3 B．11.2 C．12 D．13.4

【答案】B

【分析】根据平均数和方差公式，直接计算求值.

【详解】估算全班学生每周购买零食的支出的平均数，

方差．

故选：B．

4．某校有语文教师30人，数学教师42人，英语教师30人，现就新课程改革问题用分层抽样的方法抽取一个容量为17的样本，则数学教师被抽取的人数是（    ）

A．4 B．5 C．6 D．7

【答案】D

【分析】根据分层抽样的性质求解即可.

【详解】因为用分层抽样的方法抽取一个容量为17的样本，所以数学教师被抽取的人数是.

故选：D

5．在一次体检中，甲、乙两个班学生的身高统计如下表：

其中甲－乙＝5，则两个班学生身高的方差为（    ）

A．19 B．18 C．18.6 D．20

【答案】A

【分析】求出总平均值，再根据方差公式计算方差．

【详解】由已知，所以，

设两个班总均值为，则，

所以两个班的方差为

．

故选：A．

6．新能源汽车是指采用非常规的车用燃料作为动力来源的汽车，包括纯电动汽车和其他类型车辆（如增程式电动汽车､混合动力汽车､燃料电池电动汽车等）.具有环保､节能､效率高､使用成本低､噪音小等优势.近年来，我国新能源汽车市场飞速发展.如图所示为2015年至2021年H1（H1表示上半年）中国新能源汽车保有量统计情况，根据图中所给信息，以下说法错误的是（    ）

A．中国新能源汽车保有量在2017年首次突破百万辆

B．自2015年起至2021年H1，中国新能源汽车保有量每年都在增加

C．2016年纯电动汽车保有量增长率最大

D．相比2018年，2019年纯电动汽车保有量占新能源汽车保有量的比率降低了

【答案】D

【分析】结合表中数据，依次分析各选项即可得答案；

【详解】解：对于A选项，2015，2016，2017年中国新能源汽车保有量分别为42万辆，91万辆，153万辆，故A正确；

对于B选项，由表中数据可知，自2015年起，中国新能源汽车保有量每年都在增加，B正确；

对于C选项，由表中数据可知，2016年纯电动汽车保有量增长率大于100%，其他年份都小于100%，故C正确；

对于D选项，2019年纯电动汽车保有量占新能源汽车保有量的比率为，2018年为，计算得，故相比2018年，2019年纯电动汽车保有量占新能源汽车保有量的比率增加了.

故选：D.

7．如果数据、、、的平均值为，方差为，则数据：、、、的平均值和方差分别为（    ）

A．， B．， C．， D．，

【答案】A

【分析】计算出数据、、、的平均值和方差的值，然后利用平均数和方差公式计算出数据、、、的平均值和方差.

【详解】设数据、、、的平均值为，方差为，

由题意，得，

由方差公式得，.

所以，数据、、、的平均值为，

方差为.

故选：A.

【点睛】本题考查平均数与方差的计算，熟练利用平均数与方差的公式计算是解题的关键，考查计算能力，属于中等题.

8．已知一个容量为的样本数据的平均值为90，方差为10，若去掉其中5个为90的样本数据，剩余样本数据的平均值为，方差为，则下列结论正确的是（    ）

A．， B．，

C．， D．，

【答案】A

【分析】根据题意，其平均值不变，，再根据方差公式即可得答案.

【详解】由题意可知，个样本数据之和为，

去掉5个相同的样本数据90后，个样本数据之和为，

所以，排除选项C；

因为样本数据中有5个相同的数据90，且，

不妨设去掉的5个相同的样本数据90都排在最后，

则，

所以，即．

故选：A

二、多选题

9．某篮球爱好者在一次篮球训练中，需进行五轮投篮，每轮投篮5次.统计各轮投进球的个数，获知其前四轮投中的个数分别为2，3，4，4，则第五轮结束后下列数字特征有可能发生的是（    ）

A．平均数为3，极差是3 B．中位数是3，极差是3

C．平均数为3，方差是0.8 D．中位数是3，方差是0.56

【答案】BCD

【分析】由题知，前四轮投中的个数总和为13，从选项看，分两大类讨论：

①平均数为3，则第五轮投中2个，再根据极差和方差的计算公式求解后，即可判断选项A和C；②中位数为3，则第五轮投中的个数为0或1或2或3，然后分4种情况，逐一计算极差和方差，从而判断选项B和D．

【详解】2+3+4+4＝13，

①若平均数为3，则第五轮投中的个数为2，

所以极差为4﹣2＝2，方差为，

即选项A错误，C正确；

②若中位数为3，则第五轮投中的个数为0或1或2或3，

当投中的个数为0时，极差为4，方差为

当投中的个数为1时，极差为3，方差为；

当投中的个数为2时，极差为2，方差为0.8；

当投中的个数为3时，极差为2，方差为

即选项B和D均正确．

故选：BCD．

【点睛】此题为基础题，考查统计中相关概念.

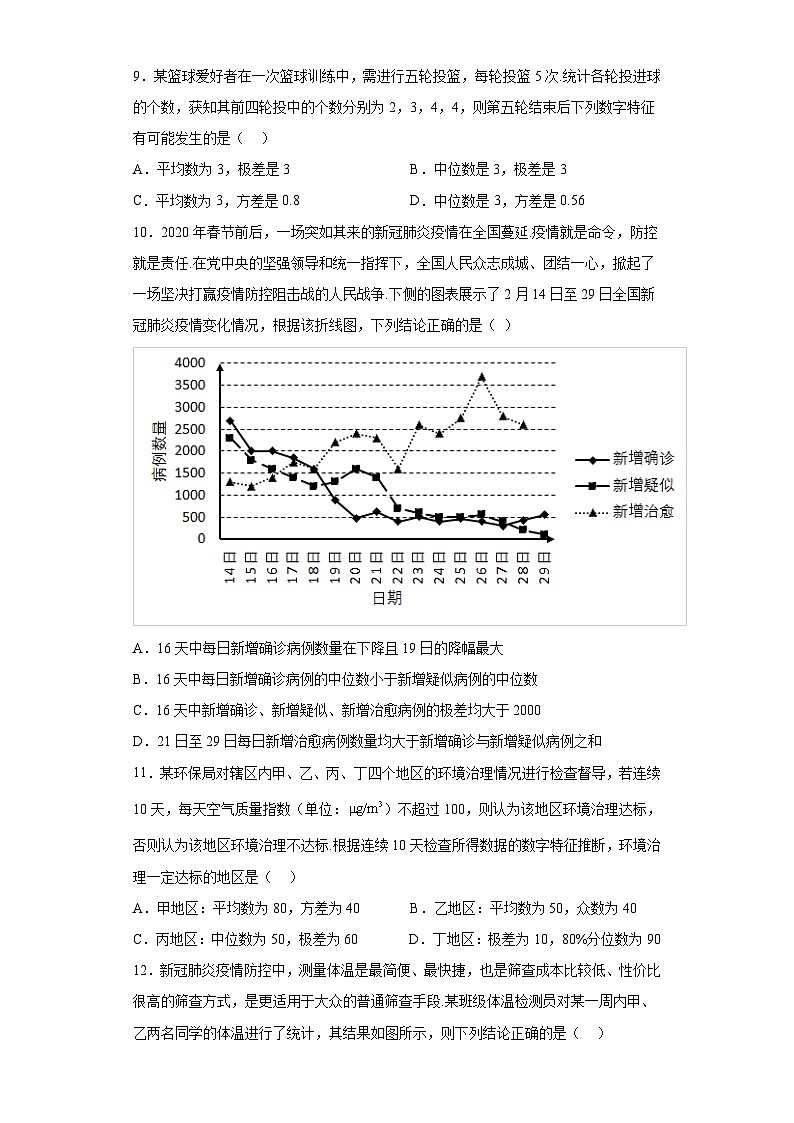
10．2020年春节前后，一场突如其来的新冠肺炎疫情在全国蔓延.疫情就是命令，防控就是责任.在党中央的坚强领导和统一指挥下，全国人民众志成城、团结一心，掀起了一场坚决打赢疫情防控阻击战的人民战争.下侧的图表展示了2月14日至29日全国新冠肺炎疫情变化情况，根据该折线图，下列结论正确的是（ ）

A．16天中每日新增确诊病例数量在下降且19日的降幅最大

B．16天中每日新增确诊病例的中位数小于新增疑似病例的中位数

C．16天中新增确诊、新增疑似、新增治愈病例的极差均大于2000

D．21日至29日每日新增治愈病例数量均大于新增确诊与新增疑似病例之和

【答案】BCD

【分析】根据折线图，中位数、极差的概念，判断各选项．

【详解】20日新增确诊病例数量比19日多，A错；

新增确诊病例的中位数小于新增疑似病例的中位数在21、22日左右，比较可得B正确；

新增确诊极差、新增疑似极差、新增治愈病例的极差，均大于2000，C正确；

21日至29日每日新增治愈病例数量均大于新增确诊与新增疑似病例之和，D正确．

故选：BCD．

【点睛】本题考查统计图表，考查折线图，中位数、极差等概念，解题关键是正确认识统计图，能从图表中抽象出所需数据，并对数据进行处理．

11．某环保局对辖区内甲、乙、丙、丁四个地区的环境治理情况进行检查督导，若连续10天，每天空气质量指数（单位：）不超过100，则认为该地区环境治理达标，否则认为该地区环境治理不达标.根据连续10天检查所得数据的数字特征推断，环境治理一定达标的地区是（    ）

A．甲地区：平均数为80，方差为40 B．乙地区：平均数为50，众数为40

C．丙地区：中位数为50，极差为60 D．丁地区：极差为10，80%分位数为90

【答案】AD

【分析】根据平均数、方差、众数、中位数、极差、百分位数的知识对选项进行分析，从而确定正确选项.

【详解】设每天的空气质量指数为，则方差.

对于A选项，由，得，

如果这10天中有1天的空气质量指数超过100，则必有矛盾，

所以这10天每天的空气质量指数都不超过100，A正确.

对于B选项，有天为40，有天为，有天为，此时：平均数为50，众数为40，

但该地区环境治理不达标，所以B选项错误.

对于C选项，第天为，后面天为，此时中位数为50，极差为60，

但该地区环境治理不达标，所以C选项错误.

对于D选项，如果最大值超过100，根据极差为10，则最小值超过90，

这与80%分位数为90矛盾，故最大值不超过100，D正确.

故选：AD

12．新冠肺炎疫情防控中，测量体温是最简便、最快捷，也是筛查成本比较低、性价比很高的筛查方式，是更适用于大众的普通筛查手段.某班级体温检测员对某一周内甲、乙两名同学的体温进行了统计，其结果如图所示，则下列结论正确的是（    ）

A．甲同学的体温的极差为0.5℃ B．甲同学的体温的众数为36.3℃

C．乙同学的体温的中位数与平均数不相等 D．乙同学的体温比甲同学的体温稳定

【答案】ABD

【分析】根据折线图，进行数据分析，对四个选项一一验证：

对于A：直接计算极差即可；

对于B：直接计算众数即可；

对于C：直接计算中位数和平均数即可判断；

对于D：从折线图上直接可以看出.

【详解】对于A：甲同学的体温的极差为℃，故A选项正确；

对于B：甲同学的体温从低到高依次为36.1℃，36.1℃，36.3℃，36.3℃，36.3℃，36.5℃，36.6℃，故众数为36.3℃，故B选项正确；

对于C：乙同学的体温从低到高依次为36.2℃，36.3℃，36.3℃，36.4℃，36.5℃，36.5℃，36.6℃，故中位数为36.4℃，而平均数也是36.4℃，故C选项错误；

对于D：从折线图上可以看出，乙同学的体温比甲同学的体温稳定，故D选项正确.

故选：ABD

三、填空题

13．某公司有工程师6人，技术员12人，技工18人，要从这些人中抽取n个人参加科技大会．如果采用系统抽样和分层抽样的方法抽取，不用剔除个体，如果参会人数增加1个，则在采用系统抽样时，需要在总体中先剔除1个个体，则n=_______.

【答案】6

【详解】试题分析：单位有技工18人，技术员12人，工程师6人，共有36人，

∵需要从这些人中抽取一个容量为n的样本；

如果采用系统抽样和分层抽样方法抽取，都不用剔除个体；

∴18，12，6，36都能被n整除，

则可以去掉A，B两个答案

如果容量增加一个，则在采用系统抽样时，需要从总体中剔除1个个体，

总体数变为37时，要剔除一个，

∴n=6

考点：分层抽样方法；系统抽样方法

14．若的方差为3，则的方差为______.

【答案】12

【详解】分析：根据方差公式计算即可．

详解：设的平均值为，则，

显然的平均值为，

∴它们的方差为

．

点睛：本题考查方差的计算，掌握方差的计算公式是解题基础，当然方差还具有如下性质：

样本数据的方差为，则样本数据的方差为．

15．随机抽取100名年龄在年龄段的市民进行问卷调查，由此得到样本的频率分布直方图如图所示，从不小于40岁的人中按年龄段分层抽样的方法随机抽取8人，则在年龄段抽取的人数为__________．

【答案】2.      

【详解】分析：根据频率分布直方图，求出样本中不小于40岁的人的频率与频数，再求用分层抽样方法抽取的人数.

详解：根据频率分布直方图，

得样本中不小于40岁的人的频率是，

所以不小于40岁的人的频数是；

从不小于40岁的人中按年龄段分层抽样的方法随机抽取8人，

在年龄段抽取的人数为，

故答案为2.

点睛：该题考查的是有关频率分布直方图的问题，在解题的过程中，需要时刻关注直方图的意义，以及相关的公式，注意频率、频数以及样本容量之间的关系，再者就是抽样过程中每个个体被抽到的概率是相等的，从而求得结果.

16．某电池厂有A，B两条生产线制造同一型号可充电电池.现采用样本量比例分配的分层随机抽样，从某天两条生产线上的成品中随机抽取样本，并测量产品可充电次数的平均数及方差，结果如下：

则20个产品组成的总样本的平均数为__________，方差为__________.

【答案】     204     28

【分析】先由平均数的定义求得，再利用方差与平均数的公式分别求得，进而求得.

【详解】依题意，设A生产线产品的样本为，平均数为，B生产线产品的样本为，平均数为，两生产线的样本为，平均数为，

则，

又，，

所以，

所以.

故答案为：.

四、解答题

17．某班从50名学生中选1人作为校运动会的志愿者为师生服务，采用下面两种选法：

选法一  将这50名学生按1～50进行编号，相应地制作50个号签，把这50个号签放在一个暗箱中搅匀，最后随机地从中抽取1个号签，与这个号签编号一致的学生入选；

选法二  将除颜色外完全相同的49个白球与1个红球放在一个暗箱中搅匀，让50名学生逐一从中摸取1球，摸到红球的学生成为志愿者．

(1)这两种选法是否都是抽签法，为什么？

(2)这两种选法每名学生被选中的可能性是否相等？

【答案】(1)选法一是抽签法，选法二不是抽签法，理由见解析

(2)可能性相等

【分析】（1）根据抽签法的特征判断；（2）两种选法中每名学生被选中的可能性相等.

【详解】（1）选法一满足抽签法的特征，是抽签法．

选法二不是抽签法，因为抽签法要求所有的号签编号互不相同，而选法二中的49个白球无法相互区分．

（2）这两种选法中每名学生被选中的可能性相等，均为．

18．在去年高考体检中，某校随机选取了20名男生，测得其身高（单位：cm）如下表．

由于统计时出现了失误，导致5、6、7、8号的身高数据丢失，先用字母a、b、c、d表示，但是已知这4人的身高都在区间内（单位：cm），且这20组身高数据的平均数，标准差．

(1)为了更好地研究本校男生的身高数据，决定用这20个数据中在区间内的数据，重新计算其平均数与方差，据此估计，高校男生身高的平均值与方差分别为多少（方差结果保留2位小数）？

(2)说明区间内的数据与原数据对比，有什么特点（主要用平均数与方差进行说明）？

（参考公式：）

【答案】(1)平均值172，方,32.67

(2)答案见解析

【分析】（1）由题先算出，故需剔除158和，新数据的平均数为：，方差为：，化简计算即可；

（2）由新数据样本数占总数据的90%可知，样本数据较集中，平均数无变化，即平均身高无变化，方差变小，即数据更集中，更具代表性.

(1)

由条件可得区间，

在区间外的数据有158和，剔除后，剩余18个数据，其平均数为：，

方差为：，

.

(2)

以内的数据与原数据对比，有以下特点：

①以内的数据的的占总数据个数的，

说明该校左右的男生身高都在区间以内；

②以内的数据与原数据对比，平均数没变，即平均身高没有变化；

③原数据的方差为49，而以内的数据的方差约为32.67，方差变小了，

说明剔除两个极端数据后，数据更趋于集中，更具有代表性.

19．本学期某校举行了有关垃圾分类知识测试活动（满分10分，分值为整数），并从该校七年级和八年级中各随机抽取40名学生的测试成绩，整理如下：

小明将样本中的成绩进行了数据处理，如表为数据处理的一部分：

根据图表，解答问题：

(1)填空：表中的______，______；

(2)你认为______年级的成绩更加稳定，理由是______；

(3)若规定6分及6分以上为合格，该校八年级共1200名学生参加了此次测试活动，估计参加此次测试活动成绩合格的学生人数是多少？

【答案】(1)7.5、7.5

(2)八，八年级成绩的方差小于七年级

(3)（人）

【分析】（1）由条形统计图求出平均数与中位数；

（2）判断七年级、八年级的方差的大少关系，即可得解；

（3）求出样本中合格学生的频率，即可估计八年级合格学生人数；

(1)

解：平均数，

因为，所以数据从小到大排列的第个数是，第个数是，

所以数据的中位数；

(2)

解：因为，，，所以八年级成绩更稳定，因为八年级成绩的方差小于七年级；

(3)

解：样本中八年级学生成绩合格的频率为，

所以估计参加此次测试活动成绩合格的学生人数是（人）；

20．从某小区抽取100户居民用户进行月用电量调查，发现他们的用电量都在50~350（单位：）之间，进行适当分组后（每组为左闭右开的区间），画出频率分布直方图如图所示：

(1)求在被调查的用户中，用电量落在区间的户数；

(2)求直方图中x的值；

(3)求这组数据的平均数.

【答案】(1)30户

(2)0.0044

(3)

【分析】（1）根据频率分布直方图估计频数即可；

（2）根据频率分布直方图的各矩形面积和为求解即可；

（3）根据频率分布直方图估计平均数即可.

(1)

解：，

所以在被调查的用户中，用电量落在区间的户数为30户

(2)

解：

所以直方图中x的值为0.0044.

(3)

解：各区间的中点值分别为：75､125､175､225､275､325，

所以这组数据的平均数为.

21．心绞痛是冠状动脉供血不足，心肌急剧地暂时缺血与缺氧所引起的以发作性胸痛或胸部不适为主要表现的临床综合征．在某地随机调查10位心绞痛患者第一次出现症状的年龄，得到如图所示的样本数据频率分布直方图．

(1)求直方图中的值；

(2)估计这组数据的平均数；（同一组中的数据以该组区间的中点值为代表）

【答案】(1)；

(2).

【分析】（1）根据频率分布直方图的性质，列出方程，即可得出的值；

（2）根据频率分布直方图中的数据，列出式子，计算即可得出答案.

【详解】（1）由频率分布直方图可知，，

所以.

（2）由频率分布直方图可知，这组数据的平均数为

.

22．某学校在上报《国家学生体质健康标准》高一年级学生的肺活量单项数据中，采用样本量按比例分配的分层随机抽样方法.如果不知道样本数据，只知道抽取了男生20人，其肺活量平均数，方差为10；抽取了女生30人，其肺活量平均数为，方差为20，估计高一年级全体学生肺活量的平均数与方差.

【答案】平均数为2700ml，方差为60016.

【分析】根据按比例分配分层抽样的平均数与各层平均数关系,即可求得总体平均数;由方程定义,即可将方差公式变形,结合和,代入两组样本的方差,即可求解.

【详解】把男生样本记为,其平均数记为,方差记为；把女生样本记为,其平均数记为,方差记为；把总样本数据的平均数记为,方差记为.

由,,根据按比例分配分层随机抽样总样本平均数与各层样本平均数的关系,可得总样本平均数为.

根据方差的定义,总样本方差为

由,可得..

同理可得.因此

据此估计高一年级全体学生肺活量的平均数为,方差为60016.

【点睛】本题考查了分层抽样中各层的平均数与方差和总体的关系,方差关系式的变形较为复杂,属于中档题.