





2022-2023学年度浙江省杭州十四中凤起康桥校区高一上学期期末数学试题
展开杭十四中2022-2023学年第一学期期末测试
高一年级数学学科试卷
考生须知:
1.本试卷分试题卷和答题卷两部分.满分150分,考试时间120分钟.
2.请用黑色字迹的钢笔或签字笔在答题卡指定的区域(黑色边框)内作答,超出答题区域的作答无效!
3.考试结束,只需上交答题卡.
一、选择题:本大题共8小题,每小题5分,共40分.每小题列出的四个选项中只有一个是符合题目要求的,不选、多选、错选均不得分.
1. 若全集![]() ,且
,且![]() ,则集合
,则集合![]() ( )
( )
A. {1,4} B. {0,4} C. {2,4} D. {0,2}
2. 命题“∀x>0,都有x2﹣x+3≤0”的否定是( )
A. ∃x>0,使得x2﹣x+3≤0 B. ∃x>0,使得x2﹣x+3>0
C. ∀x>0,都有x2﹣x+3>0 D. ∀x≤0,都有x2﹣x+3>0
3. 中国宋代的数学家秦九韶曾提出“三斜求积术”,即假设在平面内有一个三角形,边长分别为a,b,c,三角形的面积S可由公式![]() 求得,其中
求得,其中![]() 为三角形周长的一半,这个公式也被称为海伦一秦九韶公式,现有一个三角形的边长满足
为三角形周长的一半,这个公式也被称为海伦一秦九韶公式,现有一个三角形的边长满足![]() ,则此三角形面积的最大值为( )
,则此三角形面积的最大值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
4. 函数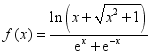 的图象大致是( )
的图象大致是( )
A. 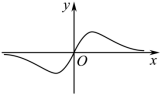 B.
B. 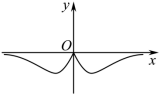
C. 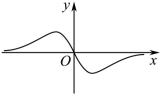 D.
D. 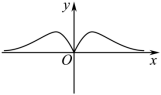
5. 若![]() ,则
,则![]() 的值为( )
的值为( )
A. 3 B. ![]() C.
C. ![]() D.
D. ![]()
6. 基本再生数![]() 与代间隔T是流行病学基本参数,其中基本再生数指一个感染者传染
与代间隔T是流行病学基本参数,其中基本再生数指一个感染者传染平均人数,代间隔指相邻两代间传染所需的平均时间,在新冠肺炎疫情初始阶段,可以用指数模型:
![]() 描述累计感染病例数
描述累计感染病例数![]() 随时间t(单位:天)的变化规律,指数增长率r与
随时间t(单位:天)的变化规律,指数增长率r与![]() ,T近似满足
,T近似满足![]() .有学者基于已有数据估计出
.有学者基于已有数据估计出![]() .据此,在新冠肺炎疫情初始阶段,累计感染病例数是原来的2倍需要的时间约为(备注:
.据此,在新冠肺炎疫情初始阶段,累计感染病例数是原来的2倍需要的时间约为(备注:![]() )( )
)( )
A. 0.9天 B. 1.8天 C. 12天 D. 3.6天
7. 设正实数![]() ,
,![]() ,
,![]() 分别满足
分别满足![]() ,则
,则![]() ,
,![]() ,
,![]() 的大小关系为( )
的大小关系为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
8. 定义在![]() 内的函数
内的函数![]() 满足
满足![]() ,且当
,且当![]() ,
,![]() 时,
时, ,对
,对![]() ,
,![]() ,
,![]() ,
,![]() ,使得
,使得![]() ,则实数
,则实数![]() 的取值范围为( )
的取值范围为( )
A. ![]() B.
B. ![]()
C
![]() ,
,![]() D.
D. ![]()
二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求全部选对的得5分,有选错的得0分,部分选对的得2分.
9. 已知函数![]() 在R上单调递减,且为奇函数,若
在R上单调递减,且为奇函数,若![]() ,则满足
,则满足![]() 的x值可能为( )
的x值可能为( )
A. ![]() B. 0 C. 1 D. 2
B. 0 C. 1 D. 2
10. 下列选项正确的是( )
A. 若![]() ,则
,则![]() 的最小值为4 B. 若
的最小值为4 B. 若![]() ,则
,则![]() 的最小值是2
的最小值是2
C. 若![]() ,则
,则![]() 的最大值为
的最大值为![]() D. 若正实数x,y满足
D. 若正实数x,y满足![]() ,则
,则![]() 的最小值为6
的最小值为6
11. 设函数![]() ,则下列结论正确的是( )
,则下列结论正确的是( )
A. 若![]() ,
,![]()
B. 存在![]() ,使
,使![]() 的图象向左平移
的图象向左平移![]() 个单位长度后得到的图象关于原点对称
个单位长度后得到的图象关于原点对称
C. 若![]() 在
在![]() 上有且仅有4个零点,则
上有且仅有4个零点,则![]() 的取值范围
的取值范围![]()
D. ![]()
![]() 上单调递增
上单调递增
12. 函数![]() ,以下四个结论正确的是( )
,以下四个结论正确的是( )
A. ![]() 的值域是
的值域是![]()
B. 对任意![]() ,都有
,都有![]()
C. 若规定![]() ,则对任意的
,则对任意的![]()
D. 对任意的![]() ,若函数
,若函数![]() 恒成立,则当
恒成立,则当![]() 时,
时,![]() 或
或![]()
三、填空题:本题共4小题,每小题5分,共20分.
13. 已知圆锥的底面半径为3,其侧面展开扇形的圆心角大小为![]() ,则这个圆锥的母线长为____________.
,则这个圆锥的母线长为____________.
14. 用![]() 表示a、b两个数中的最大值,设函数
表示a、b两个数中的最大值,设函数![]() ,若
,若![]() 恒成立,则m的最大值是____________.
恒成立,则m的最大值是____________.
15. 物体在常温下的温度变化可以用牛顿冷却规律来描述:设物体的初始温度是![]() ,经过一定时间t(单位:
,经过一定时间t(单位:![]() )后的温度是T,则
)后的温度是T,则![]() ,其中
,其中![]() 称为环境温度,h称为半衰期,现有一杯用
称为环境温度,h称为半衰期,现有一杯用![]() 热水冲的速溶咖啡,放在
热水冲的速溶咖啡,放在![]() 的房间中,如果咖啡降到
的房间中,如果咖啡降到![]() 需要
需要![]() ,那么这杯咖啡要从
,那么这杯咖啡要从![]() 降到
降到![]() ,还需要__________
,还需要__________![]() .
.
16. 设函数 ,若关于x的函数
,若关于x的函数![]() 恰好有四个零点,则实数a的取值范围是____________.
恰好有四个零点,则实数a的取值范围是____________.
四、解答题:本题共6小题,共70分解答应写出文字说明、证明过程或演算步骤.
17. 已知全集![]() ,集合
,集合![]() ,
,![]() .
.
(1)求![]()
![]() ;
;
(2)若集合![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
18. 设![]() ,已知
,已知![]() .
.
(1)求![]() 的值;
的值;
(2)求![]()
值.
19. 已知函数![]() 是定义在R上的偶函数.
是定义在R上的偶函数.
(1)求实数m的值;
(2)利用定义证明![]() 在
在![]() 上的单调性;
上的单调性;
(3)若![]() ,求实数a的取值范围.
,求实数a的取值范围.
20. 小李同学大学毕业后,决定利用所学专业进行自主创业.经过调查,生产某小型电子产品需投入年固定成本5万元,每年生产x万件,需另投入流动成本![]() 万元,在年产量不足8万件时,
万元,在年产量不足8万件时,![]() (万元);在年产量不小于8万件时,
(万元);在年产量不小于8万件时,![]() (万元).每件产品售价为10元,经分析,生产的产品当年能全部售完.
(万元).每件产品售价为10元,经分析,生产的产品当年能全部售完.
(1)写出年利润![]() (万元)关于年产量x(万件)的函数解析式.(年利润=年销售收入-固定成本-流动成本)
(万元)关于年产量x(万件)的函数解析式.(年利润=年销售收入-固定成本-流动成本)
(2)年产量为多少万件时,小李在这一产品的生产中所获利润最大?最大利润是多少?
21. 已知函数![]() .
.
(1)求![]() 的单调递增区间;
的单调递增区间;
(2)若![]() 在
在![]() 上存在最小值,求实数t的取值范围;
上存在最小值,求实数t的取值范围;
(3)方程![]() 在
在![]() 上的两解分别为
上的两解分别为![]() ,求
,求![]() 的值.
的值.
22. 已知函数![]() ,其中实数a>0且a≠1.
,其中实数a>0且a≠1.
(1)若关于x函数
![]() 在
在![]() 上存在零点,求a的取值范围;
上存在零点,求a的取值范围;
(2)求所有的正整数m的值,使得存在a∈(0,1),对任意x∈[m,7],均有不等式![]() 成立.
成立.
2022-2023学年浙江省杭州十四中凤起康桥校区高二(上)期末数学试卷(含解析): 这是一份2022-2023学年浙江省杭州十四中凤起康桥校区高二(上)期末数学试卷(含解析),共21页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年浙江省杭州第十四中学高一上学期期中数学试题(解析版): 这是一份2022-2023学年浙江省杭州第十四中学高一上学期期中数学试题(解析版),共17页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年度浙江省浙大附中丁兰校区高一上学期期末数学试题: 这是一份2022-2023学年度浙江省浙大附中丁兰校区高一上学期期末数学试题,文件包含浙江省浙大附中丁兰校区高一上学期期末数学试题原卷版docx、浙江省浙大附中丁兰校区高一上学期期末数学试题解析版docx等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。












