


数学八年级下册第1章 直角三角形1.3 直角三角形全等的判定同步训练题
展开[直角三角形全等的判定]
一、选择题
1.如图,AC=BC,AC⊥OA,CB⊥OB,则直接判定Rt△AOC≌Rt△BOC的理由是 ( )
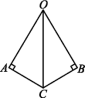
A.SSS B.ASA C.SAS D.HL
2.如图,在△ABC中,AB=AC,D是BC边的中点,DE⊥AB于点E,DF⊥AC于点F,则图中的全等三角形共有 ( )
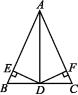
A.2对 B.3对 C.4对 D.5对
3.下列条件中,不能作出唯一直角三角形的是( )
A.已知两个锐角
B.已知两条直角边长
C.已知一条直角边长和斜边长
D.已知一个锐角和其所对直角边长
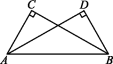
4.如图,∠ACB=∠EDB=90°,AC=ED,则下列条件中,不能判定△ABC≌△EBD的是( )

A.∠A=∠E B.AB=BD C.BC=BD D.∠ABE=∠CBD
二、填空题
5.如图,已知AC⊥BC,AD⊥BD,垂足分别是C,D,若要用“HL”得到Rt△ABC≌Rt△BAD,则应添加的条件是 (写一种即可).
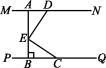
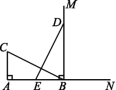
6.如图,MN∥PQ,AB⊥PQ于点B,交MN于点A,点D,C分别在直线MN与PQ上,点E在AB上,AD+BC=7,AD=BE,DE=EC,则AB= .
7.如图,已知CA⊥AB,垂足为A,AB=8米,AC=4米,射线BM⊥AB,垂足为B.一动点E从点A出发以2米/秒的速度沿射线AN运动,D为射线BM上一动点,随着点E的运动而运动,且始终保持ED=CB,当点E运动 秒时,△DEB与△BCA全等.
三、解答题
8.如图,已知∠C=∠D=90°,BC与AD交于点E,AC=BD.求证:AE=BE.
图
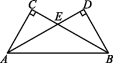
9.如图,已知AD,AF分别是钝角三角形ABC和钝角三角形ABE的高,且AD=AF,AC=AE.求证:BC=BE.
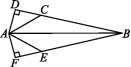
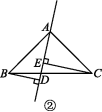
10.在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于点D,CE⊥DE于点E.
(1)若点B,C在DE的同侧(如图①所示),且AD=CE.求证:AB⊥AC.
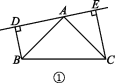
(2)若点B,C在DE的两侧(如图②所示),且AD=CE,其他条件不变,AB与AC仍垂直吗?若垂直,请给出证明;若不垂直,请说明理由.
![]()
[阅读理解与分类讨论] 问题提出:学习了全等三角形的判定方法(“SSS”“SAS”“ASA”“AAS”“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
初步思考:将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠ABC=∠DEF,则AB是否等于DE?可对∠ABC进行分类,分为“∠ABC是锐角、直角、钝角”三种情况进行探究.
第一种情况:若∠ABC是锐角,则AB不一定等于DE;
第二种情况:若∠ABC是直角,根据“HL”,可得△ABC≌△DEF,则AB=DE;
第三种情况:若∠ABC是钝角,则AB=DE.
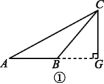
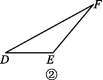
问题解决:如图,在△ABC和△DEF中,AC=DF,BC=EF,∠ABC=∠DEF,且∠ABC是钝角.求证:AB=DE.
方法归纳:化归是一种有效的数学思维方式,一般是将未解决的问题通过变换转化为已解决的问题,观察发现第三种情况可以转化为第二种情况,如图①,过点C作CG⊥AB交AB的延长线于点G.
(1)在△DEF中用尺规作出DE边上的高FH,不写作法,保留作图痕迹;
(2)请你在完成(1)中作图的基础上,证明AB=DE.
答案
1.D 2.B 3.A
4. B A项符合ASA;C项符合SAS;D项符合AAS;B项中AB与BD不是对应边.故选B.
5.答案不唯一,如BC=AD
6. 7
∵MN∥PQ,AB⊥PQ,∴AB⊥MN,
∴∠DAE=∠EBC=90°.
在Rt△ADE和Rt△BEC中,
∵DE=EC,AD=BE,
∴Rt△ADE≌Rt△BEC(HL),∴AE=BC.
∵AD+BC=7,
∴AB=BE+AE=AD+BC=7.
7. 0或2或6或8
①当点E在线段AB上,AC=BE时,△ACB≌△BED.
∵AC=4米,∴BE=4米,
∴AE=8-4=4(米),
∴点E的运动时间为4÷2=2(秒);
②当点E在射线BN上,AC=BE时,△ACB≌△BED,
∵AC=4米,∴BE=4米,
∴AE=8+4=12(米),
∴点E的运动时间为12÷2=6(秒);
③当点E在线段AB上,AB=EB时,△ACB≌△BDE,这时点E在点A处未动,因此运动时间为0秒;
④当点E在射线BN上,AB=EB时,△ACB≌△BDE,AE=8+8=16(米),点E的运动时间为16÷2=8(秒).
8.证明:在Rt△ACB和Rt△BDA中,
∵AB=BA,AC=BD,
∴Rt△ACB≌Rt△BDA(HL),
∴∠ABC=∠BAD,∴AE=BE.
9.证明:∵AD,AF分别是钝角三角形ABC和钝角三角形ABE的高,
∴∠ADC=∠AFE=90°.
在Rt△ADC和Rt△AFE中,
∵AD=AF,AC=AE,
∴Rt△ADC≌Rt△AFE(HL),∴CD=EF.
在Rt△ABD和Rt△ABF中,
∵AD=AF,AB=AB,
∴Rt△ABD≌Rt△ABF(HL),∴BD=BF,
∴BD-CD=BF-EF,即BC=BE.
10.解:(1)证明:∵BD⊥DE,CE⊥DE,
∴∠ADB=∠CEA=90°.
在Rt△ABD和Rt△CAE中,
∵AB=CA,AD=CE,
∴Rt△ABD≌Rt△CAE,
∴∠DAB=∠ECA.
∵∠EAC+∠ECA=90°,
∴∠DAB+∠EAC=90°,
∴∠BAC=180°-(∠DAB+∠EAC)=90°,∴AB⊥AC.
(2)AB与AC仍垂直.
证明:同(1)可证得Rt△ABD≌Rt△CAE,
∴∠DAB=∠ECA.
∵∠EAC+∠ECA=90°,
∴∠EAC+∠DAB=90°,即∠BAC=90°,
∴AB⊥AC.
[素养提升]
解:(1)如图所示,FH即为所作.
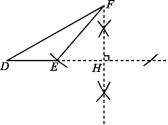
(2)证明:∵∠ABC=∠DEF,
∴∠CBG=∠FEH.
∵CG⊥AB,FH⊥DE,
∴∠BGC=∠EHF=90°.
又∵BC=EF,
∴△CBG≌△FEH(AAS),
∴BG=EH,CG=FH.
在Rt△ACG和Rt△DFH中,
∵AC=DF,CG=FH,
∴Rt△ACG≌Rt△DFH(HL),
∴AG=DH,
∴AG-BG=DH-EH,
即AB=DE.
初中数学湘教版八年级下册1.3 直角三角形全等的判定课堂检测: 这是一份初中数学湘教版八年级下册<a href="/sx/tb_c95338_t7/?tag_id=28" target="_blank">1.3 直角三角形全等的判定课堂检测</a>,共8页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
初中湘教版第1章 直角三角形1.3 直角三角形全等的判定课时作业: 这是一份初中湘教版第1章 直角三角形1.3 直角三角形全等的判定课时作业,共6页。试卷主要包含了选择题,填空题,计算题等内容,欢迎下载使用。
数学八年级下册1.3 直角三角形全等的判定优秀练习: 这是一份数学八年级下册1.3 直角三角形全等的判定优秀练习,共8页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。














