浙江省鄞州区四校联考2022-2023学年数学七年级第二学期期末教学质量检测试题含答案

浙江省鄞州区四校联考2022-2023学年数学七年级第二学期期末教学质量检测试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

考生请注意：

1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。

2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。

3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。

一、选择题(每小题3分,共30分)

1．△ABC与△DEF的相似比为，则△ABC与△DEF的面积比为（　　）

A． B． C． D．

2．点A（x1，y1），B（x2，y2），C（x3，y3）在反比例函数y= 的图象上，若x1＜x2＜0＜x3，则y1，y2，y3的大小关系是（　　）

A．y1＜y2＜y3 B．y2＜y3＜y1 C．y3＜y2＜y1 D．y2＜y1＜y3

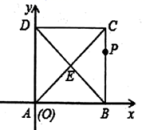
3．如图，以正方形的顶点为坐标原点，直线为轴建立直角坐标系，对角线与相交于点，为上一点，点坐标为，则点绕点顺时针旋转90°得到的对应点的坐标是(    )

A． B． C． D．

4．下列关系不是函数关系的是（　　）

A．汽车在匀速行驶过程中，油箱的余油量y（升）是行驶时间t（小时）的函数

B．改变正实数x，它的平方根y随之改变，y是x的函数

C．电压一定时，通过某电阻的电流强度I（单位：安）是电阻R（单位：欧姆）的函数

D．垂直向上抛一个小球，小球离地的高度h（单位：米）是时间t（单位：秒）的函数

5．下列说法中：①样本中的方差越小，波动越小，说明样本稳定性越好；②一组数据的众数只有一个；③一组数据的中位数一定是这组数据中的某一个数据；④数据3，3，3，3，2，5中的众数为4；⑤一组数据的方差一定是正数．其中正确的个数为(　　)

A．0 B．1 C．2 D．4

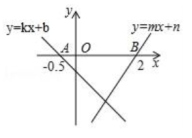
6．如图，直线与分别交x轴于点，，则不等式的解集为（    ）

A． B． C． D．或

7．若顺次连结四边形各边中点所得的四边形是菱形，则原四边形（ ）

A．一定是矩形 B．一定是菱形 C．对角线一定互相垂直 D．对角线一定相等

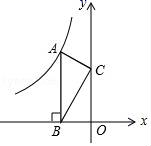
8．如图所示，点A是反比例函数y＝的图象上的一点，过点A作AB⊥x轴，垂足为B，点C为y轴上的一点，连接AC、BC．若△ABC的面积为5，则k的值为(    )

A．5 B．﹣5 C．10 D．﹣10

9．下列选择中，是直角三角形的三边长的是（　　）

A．1，2，3 B．，， C．3，4，6 D．4，5，6

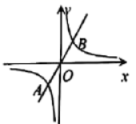
10．如图，直线与反比例函数的图象交于，两点．若点的坐标是，则点的坐标是（    ）

A． B． C． D．

二、填空题(本大题共有6小题，每小题3分，共18分)

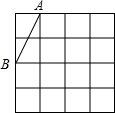
11．如图是由16个边长为1的正方形拼成的图案，任意连结这些小格点的三个顶点可得到一些三角形．与A，B点构成直角三角形ABC的顶点C的位置有___________个．

12． “两直线平行，内错角相等”的逆命题是__________．

13．函数是y关于x的正比例函数，则______．

14．将分别写有“绿色闵行”、“垃圾分类”、“要先行”的三张大小、质地相同的卡片随机排列，那么恰好排列成“绿色闵行垃圾分类要先行”的概率是__________．

15．若△ABC的三边长分别为5、13、12，则△ABC的形状是            ．

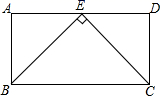
16．如图，在矩形ABCD中，E是AD的中点，且若矩形ABCD的周长为48cm，则矩形ABCD的面积为______．

三、解下列各题(本大题共8小题，共72分)

17．（8分）解不等式组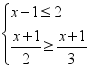，并写出不等式组的整数解.

18．（8分）一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，到达目的地后停止，设慢车行驶时间为小时，两车之间的距离为千米，两者的关系如图所示，根据图象探究：

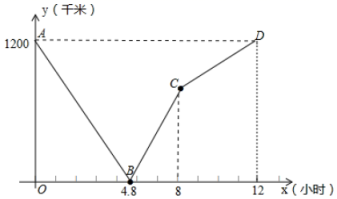
（1）看图填空：两车出发        小时，两车相遇；

（2）求快车和慢车的速度；

（3）求线段所表示的与的关系式，并求两车行驶小时两车相距多少千米．

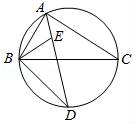
19．（8分）如图，∠BAC的平分线交△ABC的外接圆于点D，∠ABC的平分线交AD于点E．

（1）求证：DE＝DB；

（2）若∠BAC＝90°，BD＝4，求△ABC外接圆的半径．

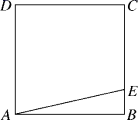
20．（8分）如图，有一块边长为40米的正方形绿地ABCD，在绿地的边BC上的E处装有健身器材，BE＝9米．有人为了走近路，从A处直接踏过绿地到达E处，小明想在A处树立一个标牌“少走■米，踏之何忍”．请你计算后帮小明在标牌的■处填上适当的数．

21．（8分）如图，在平面直角坐标系中，过点B（6，0）的直线AB与直线OA相交于点A（4，2）.

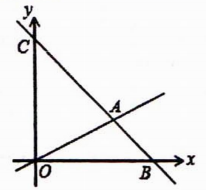
（1）求直线AB的解析式.

（2）求△OAC的面积.

（3）在y轴的负半轴上是否存在点M，使△ABM是以AB为直角边的直角角形？如果存在，求出点M的坐标；如果不存在，说明理由.

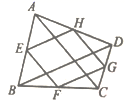
22．（10分）如图，点、、、是四边形各边的中点，、是对角线，求证：四边形是平行四边形.

23．（10分）如图所示，直线y＝－x＋8与x轴、y轴分别相交于点A，B，设M是OB上一点，若将△ABM沿AM折叠，使点B恰好落在x轴上的点B′处．

求：(1)点B′的坐标；

(2)直线AM所对应的函数表达式．

24．（12分）某市团委举办“我的中国梦”为主题的知识竞赛，甲、乙两所学校参赛人数相等，比赛结束后，发现学生成绩分别为70分，80分，90分，100分，并根据统计数据绘制了如下不完整的统计图表：

乙校成绩统计表

（1）在图①中，“80分”所在扇形的圆心角度数为；

（2）请你将图②补充完整；

（3）求乙校成绩的平均分；

（4）经计算知S甲2=135，S乙2=175，请你根据这两个数据，对甲、乙两校成绩作出合理评价．

参考答案

一、选择题(每小题3分,共30分)

1、D

2、D

3、D

4、B

5、B

6、D

7、D

8、D

9、B

10、A

二、填空题(本大题共有6小题，每小题3分，共18分)

11、1

12、内错角相等,两直线平行

13、1

14、

15、直角三角形

16、128

三、解下列各题(本大题共8小题，共72分)

17、不等式组的解集是；不等式组的整数解是.

18、（1）两车出发1.8小时相遇；（2）快车速度为；慢车速度为；（3），

19、 (1)证明见解析(2)2

20、8.

21、（1）y=﹣x+6；（2）12；（3）点M的坐标为（0，-2）或（0，-6）.

22、见解析.

23、（1）点B′的坐标为(－4，0)；（2）直线AM的函数表达式为y＝－x＋3.

24、（1）54°；（2）见解析；（3）85；（4）甲班20同名同学的成绩比较整齐．