


浙江省绍兴柯桥区七校联考2022-2023学年数学七下期末教学质量检测模拟试题含答案
展开浙江省绍兴柯桥区七校联考2022-2023学年数学七下期末教学质量检测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考试结束后,请将本试卷和答题卡一并交回.
2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.
4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.
5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗.
一、选择题(每小题3分,共30分)
1.一次函数![]() 的图象经过第二、三、四象限,则化简
的图象经过第二、三、四象限,则化简![]() 所得的结果是( )
所得的结果是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交
长为半径画弧,交![]() 于点
于点![]() ,则
,则![]() ()
()
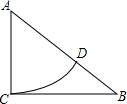
A.2.5 B.3 C.2 D.3.5
3.下列计算中,正确的是![]()
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.下列结论中,不正确的是( )
A.对角线互相垂直的平行四边形是菱形
B.对角线相等的平行四边形是矩形
C.一组对边平行,一组对边相等的四边形是平行四边形
D.对角线互相垂直的四边形面积等于对角线乘积的一半
5.如果a为任意实数, 下列各式中一定有意义的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.下图表示一次函数y=mx+n与正比例函数y=mnx(m,n是常数,且mn![]() 0)的大致图像是( )
0)的大致图像是( )
A.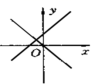 B.
B.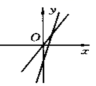
C.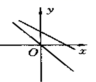 D.
D.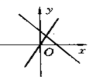
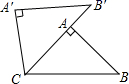
7.如图,在![]() 中,
中,![]() ,将
,将![]() 绕点C按逆时针方向旋转
绕点C按逆时针方向旋转![]() 得到
得到![]() ,点A在边
,点A在边![]() 上,则
上,则![]() 的大小为
的大小为![]()
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.点![]() ,点
,点![]() 是一次函数
是一次函数![]() 图象上的两个点,且
图象上的两个点,且![]() ,则
,则![]() 与
与![]() 的大小关系是( )
的大小关系是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.化简![]() 的结果是( )
的结果是( )
A.9 B.3 C.3![]() D.2
D.2![]()
10.如图,在同一平面直角坐标系中,一次函数y1=kx+b(k、b是常数,且k≠0)与反比例函数y2=![]() (c是常数,且c≠0)的图象相交于A(﹣3,﹣2),B(2,3)两点,则不等式y1>y2的解集是( )
(c是常数,且c≠0)的图象相交于A(﹣3,﹣2),B(2,3)两点,则不等式y1>y2的解集是( )
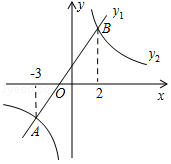
A.﹣3<x<2 B.x<﹣3或x>2 C.﹣3<x<0或x>2 D.0<x<2
二、填空题(本大题共有6小题,每小题3分,共18分)
11.设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回.设![]() 秒后两车间的距离为
秒后两车间的距离为![]() 千米,
千米,![]() 关于
关于![]() 的函数关系如图所示,则甲车的速度是______米/秒.
的函数关系如图所示,则甲车的速度是______米/秒.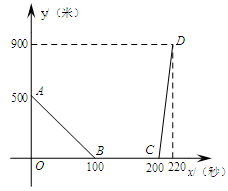
12.因式分解:![]() ___.
___.
13.不等式4x﹣6≥7x﹣15的正整数解的个数是______.
14.关于 x 的方程![]() (a≠0)的解 x=4,则
(a≠0)的解 x=4,则![]() 的值为__.
的值为__.
15.已知点P(m-3,m+1)在第二象限,则m的取值范围是_______________.
16.若m=![]() +5,则mn=___.
+5,则mn=___.
三、解下列各题(本大题共8小题,共72分)
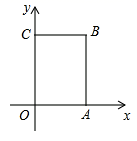
17.(8分)如图,在长方形![]() 中,
中,![]() 为平面直角坐标系的原点,点
为平面直角坐标系的原点,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,点
轴上,点![]() 在第一象限内,点
在第一象限内,点![]() 从原点出发,以每秒
从原点出发,以每秒![]() 个单位长度的速度沿着
个单位长度的速度沿着![]() 的路线移动(即沿着长方形的边移动一周).
的路线移动(即沿着长方形的边移动一周).
(1)分别求出![]() ,
,![]() 两点的坐标;
两点的坐标;
(2)当点![]() 移动了
移动了![]() 秒时,求出点
秒时,求出点![]() 的坐标;
的坐标;
(3)在移动过程中,当三角形![]() 的面积是
的面积是![]() 时,求满足条件的点
时,求满足条件的点![]() 的坐标及相应的点
的坐标及相应的点![]() 移动的时间.
移动的时间.
18.(8分)因式分解:
(1)2x3﹣8x;
(2)(x+y)2﹣14(x+y)+49
19.(8分)2019年4月25日至27日,第二届“一带一路”国际合作高峰论坛在北京举行,本届论坛期间,中国同30多个国家签署经贸合作协议。我国准备将![]() 地的茶叶1000吨和
地的茶叶1000吨和![]() 地的茶叶500吨销往“一带一路”沿线的
地的茶叶500吨销往“一带一路”沿线的![]() 地和
地和![]() 地,
地,![]() 地和
地和![]() 地对茶叶需求分别为900吨和600吨,已知从
地对茶叶需求分别为900吨和600吨,已知从![]() 、
、![]() 两地运茶叶到
两地运茶叶到![]() 、
、![]() 两地的运费(元/吨)如下表所示,设
两地的运费(元/吨)如下表所示,设![]() 地运到
地运到![]() 地的茶叶为
地的茶叶为![]() 吨,
吨,
|
|
|
| 35 | 40 |
| 30 | 45 |
(1)用含![]() 的代数式填空:
的代数式填空:![]() 地运往
地运往![]() 地的茶叶吨数为___________,
地的茶叶吨数为___________,![]() 地运往
地运往![]() 地的茶叶吨数为___________,
地的茶叶吨数为___________,![]() 地运往
地运往![]() 地的茶叶吨数为___________.
地的茶叶吨数为___________.
(2)用含![]() (吨)的代数式表示总运费
(吨)的代数式表示总运费![]() (元),并直接写出自变量
(元),并直接写出自变量![]() 的取值范围;
的取值范围;
(3)求最低总运费,并说明总运费最低时的运送方案.
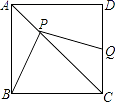
20.(8分)如图,正方形![]() ,点
,点![]() 为对角线
为对角线![]() 上一个动点,
上一个动点,![]() 为
为![]() 边上一点,且
边上一点,且![]() .
.
(1)求证:![]() ;
;
(2)若四边形![]() 的面积为25,试探求
的面积为25,试探求![]() 与
与![]() 满足的数量关系式;
满足的数量关系式;
(3)若![]() 为射线
为射线![]() 上的点,设
上的点,设![]() ,四边形
,四边形![]() 的周长为
的周长为![]() ,且
,且![]() ,求
,求![]() 与
与![]() 的函数关系式.
的函数关系式.
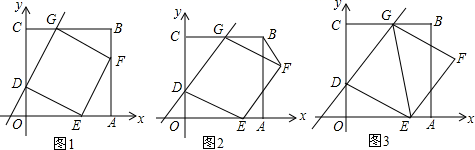
21.(8分)在平面直角坐标系xOy中,边长为6的正方形OABC的顶点A,C分别在x轴和y轴的正半轴上,直线y=mx+2与OC,BC两边分别相交于点D,G,以DG为边作菱形DEFG,顶点E在OA边上.
(1)如图1,当菱形DEFG的一顶点F在AB边上.
①若CG=OD时,求直线DG的函数表达式;
②求证:![]() OED≌
OED≌![]() BGF.
BGF.
(2)如图2,当菱形DEFG的一顶点F在AB边右侧,连接BF,设CG=a,![]() FBG面积为S.求S与a的函数关系式;并判断S的值能否等于1?请说明理由;
FBG面积为S.求S与a的函数关系式;并判断S的值能否等于1?请说明理由;
(3)如图3,连接GE,当GD平分∠CGE时,m的值为 .(直接写出答案).
22.(10分)综合与实践
(问题情境)
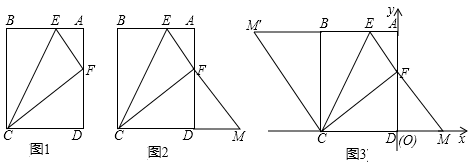
在综合与实践课上,同学们以“矩形的折叠”为主题展开数学活动,如图1,在矩形纸片ABCD中,AB=4,BC=5,点E,F分别为边AB,AD上的点,且DF=3。
(操作发现)
(1)沿CE折叠纸片,B点恰好与F点重合,求AE的长;
(2)如图2,延长EF交CD的延长线于点M,请判断△CEM的形状,并说明理由。
(深入思考)
(3)把图2置于平面直角坐标系中,如图3,使D点与原点O重合,C点在x轴的负半轴上,将△CEM沿CE翻折,使点M落在点M′处.连接CM′,求点M′的坐标.
23.(10分)如图,在![]() 中,点D、E分别是边BC、AC的中点,过点A作
中,点D、E分别是边BC、AC的中点,过点A作![]() 交DE的延长线于F点,连接AD、CF.
交DE的延长线于F点,连接AD、CF.
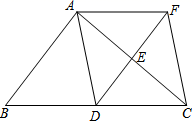
(1)求证:四边形ADCF是平行四边形;
(2)当![]() 满足什么条件时,四边形图ADCF是菱形?为什么?
满足什么条件时,四边形图ADCF是菱形?为什么?
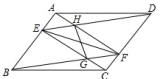
24.(12分)如图,在平行四边形ABCD中,点E.F分别在AB、CD上,AE=CF,连接AF,BF,DE,CE,分别交于H、G.
求证:(1)四边形AECF是平行四边形.(2)EF与GH互相平分.
参考答案
一、选择题(每小题3分,共30分)
1、D
2、C
3、D
4、C
5、C
6、C
7、A
8、A
9、B
10、C
二、填空题(本大题共有6小题,每小题3分,共18分)
11、20
12、2a(a-2)
13、3
14、4
15、﹣1<m<1
16、1.
三、解下列各题(本大题共8小题,共72分)
17、(1)点![]() ,点
,点![]() ;(2)点
;(2)点![]() ;(3)①P(0,5),移动时间为
;(3)①P(0,5),移动时间为![]() 秒;②P(
秒;②P(![]() ,6),移动时间为
,6),移动时间为![]() 秒;③P(4,1),移动时间为:
秒;③P(4,1),移动时间为:![]() 秒;④P(
秒;④P(![]() ,0),移动时间为:
,0),移动时间为:![]() 秒
秒
18、(1)1x(x+1)(x﹣1);(1)(x+y﹣7)1.
19、(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ;(3)由
;(3)由![]() 地运往
地运往![]() 地400吨,运往
地400吨,运往![]() 地600吨;由
地600吨;由![]() 地运往
地运往![]() 地500吨时运费最低
地500吨时运费最低
20、 (1)见解析;(2) ![]() ;(3)
;(3) ![]() .
.
21、(6)①y=2x+2;②见解析;(2)S≠6,见解析;(6)![]()
22、 (1) AE的长为![]() ;(2)ΔCEM是等腰三角形,理由见解析; (3)M′(-
;(2)ΔCEM是等腰三角形,理由见解析; (3)M′(-![]() ,5).
,5).
23、(1)见解析;(2)当△ABC是直角三角形,且∠BAC=90°时,四边形ADCF是菱形,理由见解析.
24、见解析
浙江省绍兴柯桥区七校联考2023-2024学年数学九上期末学业水平测试试题含答案: 这是一份浙江省绍兴柯桥区七校联考2023-2024学年数学九上期末学业水平测试试题含答案,共7页。试卷主要包含了答题时请按要求用笔等内容,欢迎下载使用。
浙江省绍兴柯桥区七校联考2023-2024学年九上数学期末达标测试试题含答案: 这是一份浙江省绍兴柯桥区七校联考2023-2024学年九上数学期末达标测试试题含答案,共8页。
浙江省绍兴市柯桥区六校联盟2023-2024学年数学九上期末联考试题含答案: 这是一份浙江省绍兴市柯桥区六校联盟2023-2024学年数学九上期末联考试题含答案,共7页。试卷主要包含了抛物线可由抛物线如何平移得到的,方程x2=3x的解为等内容,欢迎下载使用。












