浙江省绍兴市越城区2022-2023学年七年级数学第二学期期末质量跟踪监视试题含答案

浙江省绍兴市越城区2022-2023学年七年级数学第二学期期末质量跟踪监视试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项:

1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2．答题时请按要求用笔。

3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。

4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题(每小题3分,共30分)

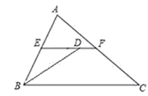
1．在△ABC中，D、E分别是BC、AC中点，BF平分∠ABC．交DE于点F．AB＝8，BC＝6，则EF的长为(　　)

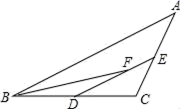
A．1 B．2 C．3 D．4

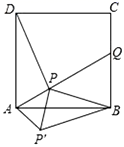
2．如图，点P是正方形内一点，连接并延长，交于点.连接，将绕点顺时针旋转90°至，连结.若，，，则线段的长为(    )

A． B．4 C． D．

3．如图，在□ABCD中，点E、F分别在边AB、DC上，下列条件不能使四边形EBFD是平行四边形的条件是（      ）

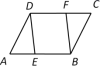
A．DE=BF B．AE=CF C．DE∥FB D．∠ADE=∠CBF

4．将直线沿轴向下平移1个单位长度后得到的直线解析式为（   ）

A． B． C． D．

5．已知四边形，对角线与交于点，从下列条件中：①；②；③；④.任取其中两个，以下组合能够判定四边形是平行四边形的是（    ）

A．①② B．②③ C．②④ D．①④

6．下列各组数中，以它们为边的三角形是直角三角形的是（    ）

A．1，2，3 B．9，16，25 C．12，15，20 D．1，2，

7．如图，在矩形纸片ABCD中，AD＝4cm，把纸片沿直线AC折叠，使点D落在E处，CE交AB于点O，若BO＝3m，则AC的长为（　　）

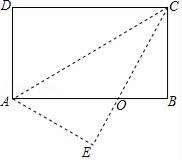
A．6cm B．8cm C．5cm D．4cm

8．在直角坐标系中，点关于原点对称的点为，则点的坐标是（     ）

A． B． C． D．

9．在某次实验中，测得两个变量m和v之间的4组对应数据如右表，则m与v之间的关系最接近于下列各关系式中的（    ）

A． B． C． D．

10．多项式与多项式的公因式是（ ）

A． B． C． D．

二、填空题(本大题共有6小题，每小题3分，共18分)

11．若,则=______

12．如图，为的中位线，平分，交于，，则的长为_______。

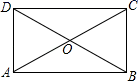
13．如图，矩形ABCD的两条对角线相交于点O，若∠AOD＝60°，AD＝2，则AC的长为_____．

14．已知中，，，直线经过点，分别过点，作直线的垂线，垂足分别为点，，若，，则线段的长为__________．

15．分解因式：=_________________________．

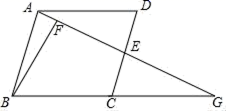
16．如图，在▱ABCD中，E为CD的中点，连接AE并延长，交BC的延长线于点G，BF⊥AE，垂足为F，若AD＝AE＝1，∠DAE＝30°，则EF＝_____．

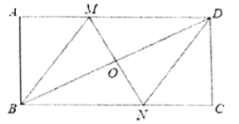
三、解下列各题(本大题共8小题，共72分)

17．（8分）如图，在矩形中，对角线的垂直平分线与相交于点，与相交于点，连接，.求证：四边形是菱形；

18．（8分） “五一”期间，小明一家乘坐高铁前往某市旅游，计划第二天租用新能源汽车自驾出游．

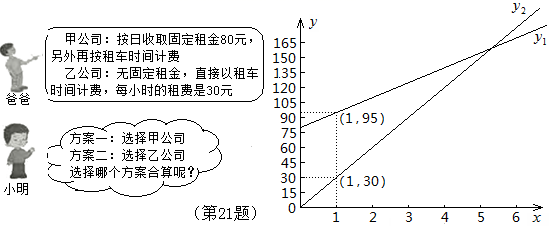[来

根据以上信息，解答下列问题：

（1）设租车时间为小时，租用甲公司的车所需费用为元，租用乙公司的车所需费用为元，分别求出，关于的函数表达式；

（2）请你帮助小明计算并选择哪个出游方案合算．

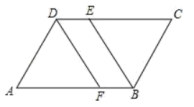
19．（8分）如图，在平行四边形中，的平分线交于点，的平分线交于点.

（1）若，，求的长.

（2）求证：四边形是平行四边形.

20．（8分）为改善生态环境，防止水土流失，某村计划在江汉堤坡种植白杨树，现甲、乙两家林场有相同的白杨树苗可供选择，其具体销售方案如下：

设购买白杨树苗x棵，到两家林场购买所需费用分别为y甲（元）、y乙（元）．

（1）该村需要购买1500棵白杨树苗，若都在甲林场购买所需费用为　   　元，若都在乙林场购买所需费用为　   　元；

（2）分别求出y甲、y乙与x之间的函数关系式；

（3）如果你是该村的负责人，应该选择到哪家林场购买树苗合算，为什么？

21．（8分）已知二次函数（，为常数）.

（1）当，时，求二次函数的最小值；

（2）当时，若在函数值的情况下，只有一个自变量的值与其对应，求此时二次函数的解析式；

（3）当时，若在自变量的值满足≤≤的情况下，与其对应的函数值的最小值为21，求此时二次函数的解析式.

22．（10分）本工作，某校对八年级一班的学生所穿校服型号情况进行了摸底调查，并根据调查结果绘制了如图所示的两幅不完整的统计图（校服型号以身高作为标准，共分为6种型号）。

条形统计图

扇形统计图

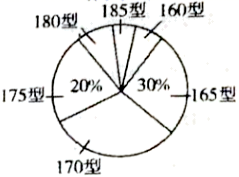
根据以上信息，解答下列问题：

（1）该班共有多少名学生？其中穿型校服的学生有多少名？

（2）在条形统计图中，请把空缺部分补充完整；

（3）在扇形统计图中，请计算型校服所对应的扇形圆心角的大小；

（4）求该班学生所穿校服型号的中位数。

23．（10分）本学期开学后，某校为了宣传关于新冠肺炎的防控知识，需印制若干份资料，印刷厂有甲、乙两种收费方式，甲种方式每份资料收费0.1元，另需收取制版费20元；乙种方式每份资料收费0.15元，不需要收取制版费．

（1）设资料印刷的费用为y元，印刷的数量为x份，请分别写出两种收费方式下y与x之间的函数关系式；

（2）该校某年级每次需印制100～600（含100和600）份资料，选择哪种印刷方式较合算？

24．（12分）已知y是x的函数，自变量x的取值范围是，下表是y与x的几组对应值．

小华根据学习函数的经验，利用上述表格所反映出的y与x之间的变化规律，对该函数的图象与性质进行了探究．下面是小华的探究过程，请将其补充完整：

（1）如图，在平面直角坐标系xOy中，描出了以上表中各组对应值为坐标的点．根据描出的点，画出该函数的图象．

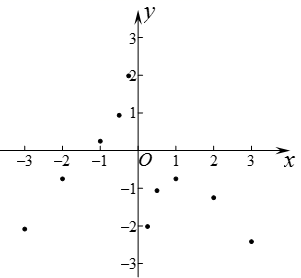
（2）根据画出的函数图象，写出：

①时，对应的函数值y约为          （结果精确到0.01）；

②该函数的一条性质：                                                  ．

参考答案

一、选择题(每小题3分,共30分)

1、A

2、D

3、A

4、A

5、D

6、D

7、D

8、B

9、B

10、A

二、填空题(本大题共有6小题，每小题3分，共18分)

11、

12、

13、1

14、或

15、．

16、﹣1

三、解下列各题(本大题共8小题，共72分)

17、见解析

18、（1）y1=15x+80（x≥0）；y2=30x（x≥0）；（2）当租车时间为小时，选择甲乙公司一样合算；当租车时间小于小时，选择乙公司合算；当租车时间大于小时，选择甲公司合算．

19、（1）；（2）证明见解析.

20、（1）5900，6000；（2）见解析；（3）当0≤x≤1000或x=3000时，两家林场购买一样，当1000＜x＜3000时，到甲林场购买合算；当x＞3000时，到乙林场购买合算．

21、（1）二次函数取得最小值-1；（2）或；

（3）或．

22、（1）50，10；（2）见解析；（3）14.4°；（4）170型

23、（1）y1＝0.1x＋20；y2＝0.15x；（2）当100≤x＜400时，选择乙种方式较合算；当x＝400时，甲、乙两种方式一样合算；当400＜x≤600时，选择甲种方式较合算

24、（1）见解析；（2）①-2.01（答案不唯一）；②y随x的增大而增大（答案不唯一）