2022-2023学年浙江省宁波市东钱湖九校七年级数学第二学期期末质量跟踪监视试题含答案

2022-2023学年浙江省宁波市东钱湖九校七年级数学第二学期期末质量跟踪监视试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

考生请注意：

1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。

2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。

3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

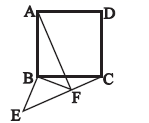
1．如图，以正方形的顶点为直角顶点，作等腰直角三角形，连接、，当、、三点在--条直线上时，若，，则正方形的面积是(    )

A． B． C． D．

2．下列二次根式是最简二次根式的是

A． B． C． D．

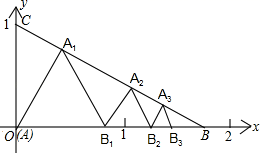
3．如图所示，已知：点A（0，0），B（，0），C（0，1）．在△ABC内依次作等边三角形，使一边在x轴上，另一个顶点在BC边上，作出的等边三角形分别是第1个△AA1B1，第2个△B1A2B2，第3个△B2A3B3，…，则第n个等边三角形的边长等于（　　）

A． B． C． D．

4．函数中自变量x的取值范围是（ ）

A． B．且 C．x＜2且 D．

5．以下列长度为边长的三角形是直角三角形的是（　　）

A．5，6，7 B．7，8，9 C．6，8，10 D．5，7，9

6．矩形不具备的性质是(     )

A．对角线相等 B．四条边一定相等

C．是轴对称图形 D．是中心对称图形

7．若ab＞0，ac＜0，则一次函数的图象不经过下列个象限（　　）

A．第一象限 B．第二象限 C．第三象限 D．第四象限

8．如图，第一个图形中有4个“”，第二个图形中有7个“”，第三个图形中有11个“”，按照此规律下去，第8个图形中“”的个数为（   ）.

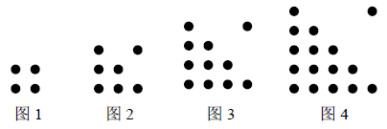
A．37 B．46 C．56 D．67

9．若分式有意义，则x应满足的条件是（　　）

A．x≠0 B．x＝2 C．x＞2 D．x≠2

10．如图，平行四边形ABCD中，AC⊥AB，点E为BC边中点，AD=6，则AE的长为（    ）

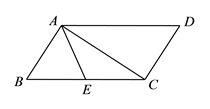
A．2 B．3     C．4     D． 5

11．若反比例函数y＝(k≠0)的图象经过点P(﹣2，6)，则k的值是(   )

A．﹣3 B．3 C．12 D．﹣12

12．要使二次根式有意义，则x的取值范围是（   ）

A．x≥1 B．x≤1 C．x>1 D．x<1

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13．如图，已知△ABC∽△ADB，若AD＝2，CD＝2，则AB的长为_____．

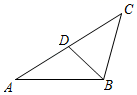
14．如图，OP=1，过P作PP1⊥OP且PP1=1，得OP1=；再过P1作P1P2⊥OP1且P1P2=1，得OP2=；又过P2作P2P3⊥OP2且P2P3=１，得OP3=2…依此法继续作下去，得=____．

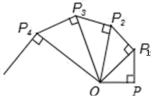
15．已知直线y=2x﹣5经过点A（a，1﹣a），则A点落在第_____象限．

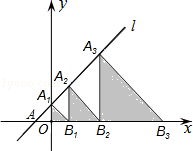
16．如图，在平面直角坐标系中，直线l：y=x+2交x轴于点A，交y轴于点A1，点A2，A3，…在直线l上，点B1，B2，B3，…在x轴的正半轴上，若△A1OB1，△A2B1B2，△A3B2B3，…，依次均为等腰直角三角形，直角顶点都在x轴上，则第n个等腰直角三角形AnBn﹣1Bn顶点Bn的横坐标为________________．

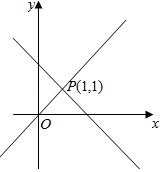
17．如图，已知函数y＝ax+b和y＝kx的图象交于点P，则根据图象可得，关于 的二元一次方程组的解是_____．

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18．（5分）在课外活动中，我们要研究一种四边形--筝形的性质．

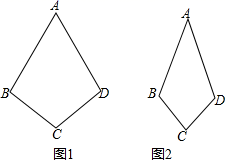
定义：两组邻边分别相等的四边形是筝形（如图1）．

小聪根据学习平行四边形、菱形、矩形、正方形的经验，对筝形的性质进行了探究．

下面是小聪的探究过程，请补充完整：

（1）根据筝形的定义，写出一种你学过的四边形满足筝形的定义的是        ；

（2）通过观察、测量、折叠等操作活动，写出两条对筝形性质的猜想，并选取其中的一条猜想进行证明；

（3）如图2，在筝形ABCD中，AB=4，BC=2，∠ABC=120°，求筝形ABCD的面积．

19．（5分）化简：（）÷并解答：

（1）当x=1+时，求原代数式的值；

（2）原代数式的值能等于﹣1吗？为什么？

20．（8分）在直角坐标系中，反比例函数y＝(x＞0)，过点A(3，4)．

(1)求y关于x的函数表达式．

(2)求当y≥2时，自变量x的取值范围．

(3)在x轴上有一点P(1，0)，在反比例函数图象上有一个动点Q，以PQ为一边作一个正方形PQRS，当正方形PQRS有两个顶点在坐标轴上时，画出状态图并求出相应S点坐标．

21．（10分）如图，，平分，且交于点，平分，且交于点，与相交于点，连接

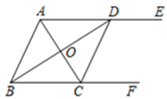
（1）求证：四边形是菱形．

（2）若，，求的长．

22．（10分）解下列方程

（1）；（2）

23．（12分）据某市交通运管部门月份的最新数据，目前该市市面上的共享单车数量已达万辆，共享单车也逐渐成为高校学生喜爱的“绿色出行”方式之一．某高校为了解本校学生出行使用共享单车的情况，随机调查了某天部分出行学生使用共享单车的情况，并整理成如下统计表．

（1）求这天部分出行学生使用共享单车次数的平均数，中位数和众数．

（2）若该校这天有名学生出行，估计使用共享单车次数在次以上（含次）的学生数．

参考答案

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1、C

2、B

3、A

4、B

5、C

6、B

7、C

8、B

9、D

10、B

11、D

12、A

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13、2．

14、

15、四．

16、 ．

17、x=1,y=1

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18、（1）菱形；（2）筝形是轴对称图形；筝形的对角线互相垂直；筝形的一组对角相等．证明见解析；（3）4．

19、（1）+1（2）不能

20、（1）；（2）当时，自变量的取值范围为；（3）①，②，③，④，．

21、（1）见解析；（2）AD＝．

22、（1）；（2）

23、（1）中位数是次,众数是次;（2）人．