


2022-2023学年浙江省杭州市高桥数学七年级第二学期期末质量跟踪监视试题含答案
展开2022-2023学年浙江省杭州市高桥数学七年级第二学期期末质量跟踪监视试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
请考生注意:
1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若关于![]() 的一元二次方程
的一元二次方程![]() 的常数项为0,则
的常数项为0,则![]() 的值等于( )
的值等于( )
A.1 B.3 C.1或3 D.0
2.某中学随机地调查了50名学生,了解他们一周在校的体育锻炼时间,结果如下表所示:
时间(小时) | 5 | 6 | 7 | 8 |
人数 | 10 | 15 | 20 | 5 |
则这50名学生这一周在校的平均体育锻炼时间是( )
A.6.2小时 B.6.4小时 C.6.5小时 D.7小时
3.将直线y=2x向右平移2个单位,再向上移动4个单位,所得的直线的解析式是( )
A.y=2x B.y=2x+2 C.y=2x﹣4 D.y=2x+4
4.下列说法正确的是( ).
A.掷一颗骰子,点数一定小于等于6;
B.抛一枚硬币,反面一定朝上;
C.为了解一种灯泡的使用寿命,宜采用普查的方法;
D.“明天的降水概率为90%”,表示明天会有90%的地方下雨.
5.下列二次根式计算正确的是( )
A.![]() -
-![]() =1 B.
=1 B.![]() +
+![]() =
=![]() C.
C.![]() ×
×![]() =
=![]() D.
D.![]() ÷
÷![]() =
=![]()
6.宁宁所在的班级有42人,某次考试他的成绩是80分,若全班同学的平均分是78分,判断宁宁成绩是否在班级属于中等偏上,还需要了解班级成绩的( )
A.中位数 B.众数 C.加权平均数 D.方差
7.从﹣4,﹣3,﹣2,﹣1,0,1,3,4,5这九个数中,随机抽取一个数,记为a,则数a使关于x的不等式组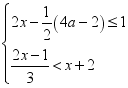 至少有四个整数解,且关于x的分式方程
至少有四个整数解,且关于x的分式方程![]() =1有非负整数解的概率是( )
=1有非负整数解的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.如图,下列哪组条件不能判定四边形ABCD是平行四边形( )
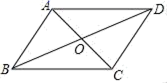
A.AB∥CD,AB=CD B.AB∥CD,AD∥BC
C.OA=OC,OB=OD D.AB∥CD,AD=BC
9.如图,在![]() 中,
中,![]() ,
,![]() ,分别以AC,BC为边向
,分别以AC,BC为边向![]() 外作正方形,两个正方形的面积分别记为
外作正方形,两个正方形的面积分别记为![]() ,
,![]() ,则
,则![]() 等于( )
等于( )

A.30 B.150 C.200 D.225
10.如图,在四边形ABCD中,对角线AC,BD相交于点O,AB∥CD,添加下列条件不能使四边形ABCD成为平行四边形的是( )
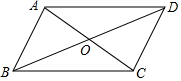
A.AB=CD B.OB=OD
C.∠BCD+∠ADC=180° D.AD=BC
11.下列调查中,最适合采用全面调查(普查)方式的是( )
A.对无锡市空气质量情况的调查 B.对某校七年级(![]() )班学生视力情况的调查
)班学生视力情况的调查
C.对某批次手机屏使用寿命的调查 D.对全国中学生每天体育锻炼所用时间的调查
12.如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是( )
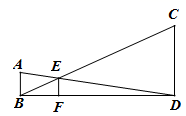
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(每题4分,满分20分,将答案填在答题纸上)
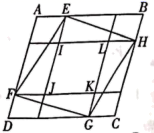
13.如图,直线![]() 、
、![]() 、
、![]() 、
、![]() 互相平行,直线
互相平行,直线![]() 、
、![]() 、
、![]() 、
、![]() 互相平行,四边形
互相平行,四边形![]() 面积为
面积为![]() ,四边形
,四边形![]() 面积为
面积为![]() ,则四边形
,则四边形![]() 面积为__________.
面积为__________.
14.方程![]() 的解为:___________.
的解为:___________.
15.若![]() 有意义,则m能取的最小整数值是__.
有意义,则m能取的最小整数值是__.
16.实施素质教育以来,某中学立足于学生的终身发展,大力开发课程资源,在七年级设立六个课外学习小组,下面是七年级学生参加六个学习小组的统计表和扇形统计图,请你根据图表中提供的信息回答下列问题.
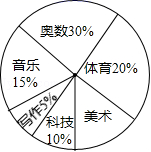
学习小组 | 体育 | 美术 | 科技 | 音乐 | 写作 | 奥数 |
人数 | 72 |
| 36 | 54 | 18 |
|
(1)七年级共有学生 人;
(2)在表格中的空格处填上相应的数字;
(3)表格中所提供的六个数据的中位数是 ;
(4)众数是 .
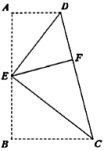
17.如图,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 上一点,分别以
上一点,分别以![]() ,
,![]() 为折痕将两个角(
为折痕将两个角(![]() ,
,![]() )向内折起,点
)向内折起,点![]() ,
,![]() 恰好都落在
恰好都落在![]() 边的点
边的点![]() 处.若
处.若![]() ,
,![]() ,则
,则![]() ________.
________.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)某公司计划购买A,B两种型号的机器人搬运材料.已知A型机器人比B型机器人每小时多搬运30kg材料,且A型机器人搬运1000kg材料所用的时间与B型机器人搬运800kg材料所用的时间相同.
(1)求A,B两种型号的机器人每小时分别搬运多少材料;
(2)该公司计划采购A,B两种型号的机器人共20台,要求每小时搬运材料不得少于2800kg,则至少购进A型机器人多少台?
19.(5分)如图,在正方形![]() 中,已知
中,已知![]() 于
于![]() .
.
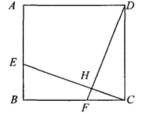
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的长.
的长.
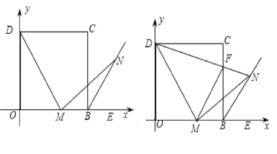
20.(8分)在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括点O、B),作MN⊥DM,垂足为M,交∠CBE的平分线于点N.
(1)写出点C的坐标;
(2)求证:MD=MN;
(3)连接DN交BC于点F,连接FM,下列两个结论:①FM的长度不变;②MN平分∠FMB,其中只有一个结论是正确的,请你指出正确的结论,并给出证明
21.(10分)光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台,先将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.两地区与该农机租赁公司商定的每天的租赁价格见表:
| 每台甲型收割机的租金 | 每台乙型收割机的租金 |
A地区 | 1800 | 1600 |
B地区 | 1600 | 1200 |
(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79 600元,说明有多少种分配方案,并将各种方案设计出来;
(3)如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提一条合理化建议.
22.(10分)解方程:
(1)2x2﹣3x+1=1.
(2)x2﹣8x+1=1.(用配方法)
23.(12分)计算:(1)![]()
(2)(![]() ﹣1)2﹣(
﹣1)2﹣(![]() ﹣
﹣![]() )(
)(![]() +
+![]() )
)
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、B
2、B
3、A
4、A
5、C
6、A
7、C
8、D
9、D
10、D
11、B
12、C
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、1
14、![]() ,
,![]()
15、1
16、(1)360;(2)1,108,20%;(3)63;(4)1.
17、![]()
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)A型机器人每小时搬运150千克材料,B型机器人每小时搬运120千克材料;(2)至少购进A型机器人14台.
19、(1)见解析;(2)![]()
20、(1)点![]() 的坐标为
的坐标为![]() ;(2)见解析;(3)MN平分∠FMB成立,证明见解析
;(2)见解析;(3)MN平分∠FMB成立,证明见解析
21、(1)y=200x+74000(10≤x≤30)
(2)有三种分配方案,
方案一:派往A地区的甲型联合收割机2台,乙型联合收割机28台,其余的全派往B地区;
方案二:派往A地区的甲型联合收割机1台,乙型联合收割机29台,其余的全派往B地区;
方案三:派往A地区的甲型联合收割机0台,乙型联合收割机30台,其余的全派往B地区;
(3)派往A地区30台乙型联合收割机,20台甲型联合收割机全部派往B地区,使该公司50台收割机每天获得租金最高.
22、(1)x1=![]() ,x2=1;(2)x1=4+
,x2=1;(2)x1=4+![]() ,x2=4﹣
,x2=4﹣![]()
23、(1)![]() ;(2)
;(2)![]()
浙江省杭州市育才中学2023-2024学年数学九上期末质量跟踪监视试题含答案: 这是一份浙江省杭州市育才中学2023-2024学年数学九上期末质量跟踪监视试题含答案,共8页。
2023-2024学年浙江省杭州市西溪中学九上数学期末质量跟踪监视模拟试题含答案: 这是一份2023-2024学年浙江省杭州市西溪中学九上数学期末质量跟踪监视模拟试题含答案,共7页。试卷主要包含了二次函数y=ax2+bx+c,方程的根是等内容,欢迎下载使用。
2023-2024学年浙江省杭州市富阳区城区联考数学九上期末质量跟踪监视试题含答案: 这是一份2023-2024学年浙江省杭州市富阳区城区联考数学九上期末质量跟踪监视试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,下列命题中,为真命题的是,下列说法正确的是,如果,那么代数式的值是.等内容,欢迎下载使用。












