


2022-2023学年浙江省温州市秀山中学数学七年级第二学期期末质量跟踪监视试题含答案
展开2022-2023学年浙江省温州市秀山中学数学七年级第二学期期末质量跟踪监视试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
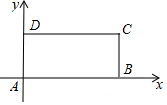
1.已知平面上四点![]() ,
,![]() ,
,![]() ,
,![]() ,一次函数
,一次函数![]() 的图象将四边形ABCD分成面积相等的两部分,则
的图象将四边形ABCD分成面积相等的两部分,则![]()
![]()
A.2 B.![]() C.5 D.6
C.5 D.6
2.一元二次方程![]() 的求根公式是( )
的求根公式是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.下列调查中,适宜采用抽样调查方式的是( )
A.调查八年级某班学生的视力情况
B.调查乘坐飞机的旅客是否携带违禁物品
C.调查某品牌LED灯的使用寿命
D.学校在给学生订制校服前尺寸大小的调查
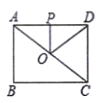
4.如图,矩形![]() 的周长是28,点
的周长是28,点![]() 是线段
是线段![]() 的中点,点
的中点,点![]() 是
是![]() 的中点,
的中点,![]() 的周长与
的周长与![]() 的周长差是2(且
的周长差是2(且![]() ),则
),则![]() 的周长为( )
的周长为( )
A.12 B.14 C.16 D.18
5.下列调查方法合适的是( )
A.为了了解冰箱的使用寿命,采用普查的方式
B.为了了解全国中学生的视力状况,采用普查的方式
C.为了了解人们保护水资源的意识,采用抽样调查的方式
D.对“神舟十一号载人飞船”零部件的检查,采用抽样调查的方式
6.若点(3,1)在一次函数y=kx-2(k≠0)的图象上,则k的值是( )
A.5 B.4 C.3 D.1
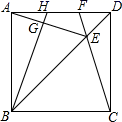
7.如图,在正方形ABCD中,E是对角线BD上一点,且满足![]() =AD,连接CE并延长交AD于点F,连接AE,过B点作
=AD,连接CE并延长交AD于点F,连接AE,过B点作![]() 于点G,延长BG交AD于点H. 在下列结论中:①AH=DF;②∠AEF=45°;③
于点G,延长BG交AD于点H. 在下列结论中:①AH=DF;②∠AEF=45°;③![]() . 其中不正确的结论有( )
. 其中不正确的结论有( )
A.1个 B.2个 C.3个 D.0个
8.已知△ABC的三边之长分别为a、1、3,则化简|9-2a|-![]() 的结果是( )
的结果是( )
A.12-4a B.4a-12 C.12 D.-12
9.若关于![]() 的分式方程
的分式方程![]() 的根是正数,则实数
的根是正数,则实数![]() 的取值范围().
的取值范围().
A.且![]() B.
B.![]() 且
且![]()
C.![]() 且
且![]() D.
D.![]() 且
且![]()
10.某水资源保护组织对邢台某小区的居民进行节约水资源的问卷调查.某居民在问卷的选项代号上画“√”,这个过程是收集数据中的( )
A.确定调查范围 B.汇总调查数据
C.实施调查 D.明确调查问题
11.下列图形是中心对称图形的是( )
A. B.
B.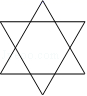 C.
C.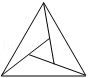 D.
D.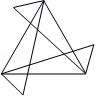
12.若将直角三角形的两直角边同时扩大2倍,则斜边扩大为原来的
A.2倍 B.3倍 C.4倍 D.5倍
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.已知平行四边形ABCD中,![]() ,
,![]() ,AE为BC边上的高,且
,AE为BC边上的高,且![]() ,则平行四边形ABCD的面积为________.
,则平行四边形ABCD的面积为________.
14.在▱ABCD中,∠BAD的平分线AE把边BC分成5和6两部分,则▱ABCD的周长为_____.
15.关于 x 的方程 x2+5x+m=0 的一个根为﹣2,则另一个根是________ .
16.计算![]() -
-![]() 的结果是_________.
的结果是_________.
17.在实数范围内分解因式:5-x2=_____.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)某花卉种植基地准备围建一个面积为100平方米的矩形苗圃园园种植玫瑰花,其中一边靠墙,另外三边用29米长的篱笆围成.已知墙长为18米,为方便进入,在墙的对面留出1米宽的门(如图所示),求这个苗圃园垂直于墙的一边长为多少米?
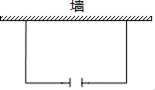
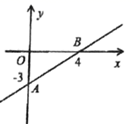
19.(5分)如图,已知一次函数的图象经过A(0,-3)、B(4,0)两点.
(1)求这个一次函数的解析式;
(2)若过O作OM⊥AB于M,求OM的长.
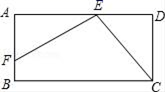
20.(8分)如图,已知矩形ABCD中,E是AD上一点,F是AB上的一点,EF⊥EC,且EF=EC.
(1)求证:△AEF≌△DCE.
(2)若DE=4cm,矩形ABCD的周长为32cm,求AE的长.
21.(10分)计算:
(1)![]() ﹣
﹣![]() ;
;
(2)![]()
22.(10分)如图,直线![]() 的函数解析式为
的函数解析式为![]() ,且
,且![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过点
经过点![]() 、
、![]() ,直线
,直线![]() 、
、![]() 交于点
交于点![]() .
.
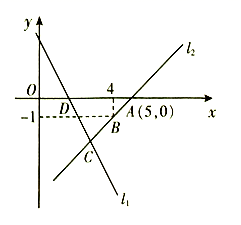
(1)求直线![]() 的函数解析式;
的函数解析式;
(2)求![]() 的面积;
的面积;
(3)在直线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 面积是
面积是![]() 面积的
面积的![]() 倍?如果存在,请求出
倍?如果存在,请求出![]() 坐标;如果不存在,请说明理由.
坐标;如果不存在,请说明理由.
23.(12分)某校在一次大课间活动中,采用了四种活动形式:A:跑步;B:跳绳;C:做操;D:游戏,全校学生都选择了一种形式参与活动,小明对同学们选择的活动形式进行了随机抽样调查,并绘制了不完整的两幅统计图,结合统计图,回答下列问题:
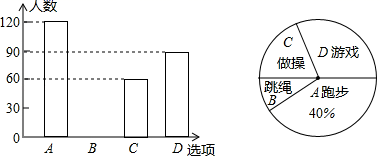
(1)本次调查学生共 人,并将条形图补充完整;
(2)如果该校有学生2000人,请你估计该校选择“跑步”这种活动的学生约有多少人?
(3)学校在每班A、B、C、D四种活动形式中,随机抽取两种开展活动,求每班抽取的两种形式恰好是“做操”和“跳绳”的概率.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、B
2、A
3、C
4、A
5、C
6、D
7、A
8、A
9、D
10、C
11、B
12、A
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、2或1
14、32或1
15、![]()
16、2
17、(![]() +x)(
+x)(![]() -x)
-x)
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、10米
19、(1)y=![]() x-3;(2)OM=
x-3;(2)OM=![]() .
.
20、(1)证明见解析;(2)6cm.
21、(1)![]() ﹣
﹣![]() ;(2)13﹣4
;(2)13﹣4![]() .
.
22、(1)![]() ;(2)3;(3)在直线
;(2)3;(3)在直线![]() 上存在点
上存在点![]() 或
或![]() ,使得
,使得![]() 面积是
面积是![]() 面积的
面积的![]() 倍.
倍.
23、(1)300;(2)选择“跑步”这种活动的学生约有800人;(3)![]()
2022-2023学年重庆市巫溪中学数学七年级第二学期期末质量跟踪监视模拟试题含答案: 这是一份2022-2023学年重庆市巫溪中学数学七年级第二学期期末质量跟踪监视模拟试题含答案,共7页。
2022-2023学年浙江省温州市苍南县数学七年级第二学期期末质量跟踪监视模拟试题含答案: 这是一份2022-2023学年浙江省温州市苍南县数学七年级第二学期期末质量跟踪监视模拟试题含答案,共7页。试卷主要包含了若分式有意义,则x,y满足,下列说法不正确的是,一元二次方程 x2= x的根是等内容,欢迎下载使用。
2022-2023学年浙江省温州市五校七年级数学第二学期期末质量跟踪监视试题含答案: 这是一份2022-2023学年浙江省温州市五校七年级数学第二学期期末质量跟踪监视试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,下列方程中是二项方程的是,在平面直角坐标系中,点在等内容,欢迎下载使用。












