


浙江省绍兴市名校2022-2023学年七年级数学第二学期期末监测模拟试题含答案
展开浙江省绍兴市名校2022-2023学年七年级数学第二学期期末监测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型(B)填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。
2.作答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。答案不能答在试题卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。不按以上要求作答无效。
4.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1.二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>-1时,y的值随x值的增大而增大.其中正确的结论有( )
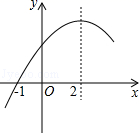
A.1个 B.2个 C.3个 D.4个
2.下列根式是最简二次根式的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知分式![]() 的值等于零,则x的值为( )
的值等于零,则x的值为( )
A.﹣2 B.﹣3 C.3 D.±3
4.如图,![]() 中,
中,![]() ,AD平分
,AD平分![]() ,点E为AC的中点,连接DE,若
,点E为AC的中点,连接DE,若![]() 的周长为26,则BC的长为
的周长为26,则BC的长为![]()
![]()
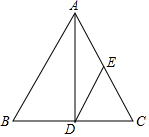
A.20 B.16 C.10 D.8
5.如图,在△ABC中,AB=AD=DC,∠B=70°,则∠C的度数为( )
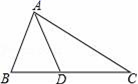
A.35° B.40° C.45° D.50°
6.某校办工厂生产的某种产品,今年产量为200件,计划通过改革技术,使今后两年的产量都比前一年增长一个相同的百分数,使得三年的总产量达到1 400件.若设这个百分数为![]() ,则可列方程( )
,则可列方程( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.如图,![]() 中,
中,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转得到
逆时针旋转得到![]() ,若点
,若点![]() 的对应点
的对应点![]() 落在
落在![]() 边上,则旋转角为( )
边上,则旋转角为( )
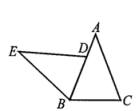
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.一个多边形的每个内角都等于108°,则这个多边形的边数为( ).
A.5 B.6 C.7 D.8
9.在![]() 中,斜边
中,斜边![]() ,则
,则![]()
![]()
A.10 B.20 C.50 D.100
10.已知一次函数y=kx+b(k≠0)图象经过第二、三、四象限,则一次函数y=﹣bx+kb图象可能是( )
A.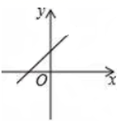 B.
B.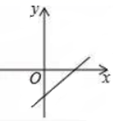 C.
C.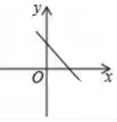 D.
D.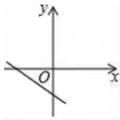
二、填空题(本大题共有6小题,每小题3分,共18分)
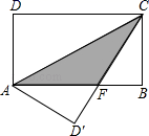
11.如图,矩形ABCD中,AB=16cm,BC=8cm,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为______.
12.如图,正方形![]() 和正方形
和正方形![]() 中,点
中,点![]() 在
在![]() 上,
上,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,那么
的中点,那么![]() 的长是__________(用含
的长是__________(用含![]() 、
、![]() 的代数式表示).
的代数式表示).
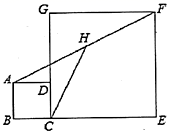
13.如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处,点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:①∠EBG=45°;②S△ABG=![]() S△FGH;③△DEF∽△ABG;④AG+DF=FG.其中正确的是_____.(把所有正确结论的序号都选上)
S△FGH;③△DEF∽△ABG;④AG+DF=FG.其中正确的是_____.(把所有正确结论的序号都选上)
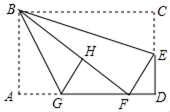
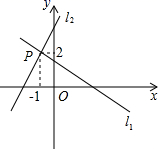
14.已知一次函数y=-x+1与y=kx+b的图象在同一直角坐标系中的位置如图(直线l1和l2),它们的交点为P,那么关于x的不等式-x+1>kx+b的解集为______.
15.计算:(-2019)0×5-2=________.
16.求代数式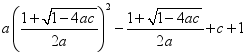 的值是____________.
的值是____________.
三、解下列各题(本大题共8小题,共72分)
17.(8分)近些年全国各地频发雾霾天气,给人民群众的身体健康带来了危害,某商场看到商机后决定购进甲、乙两种空气净化器进行销售.若每台甲种空气净化器的进价比每台乙种空气净化器的进价少300元,且用6000元购进甲种空气净化器的数量与用7500元购进乙种空气净化器的数量相同.
(1)求每台甲种空气净化器、每台乙种空气净化器的进价分别为多少元?
(2)若该商场准备进货甲、乙两种空气净化器共30台,且进货花费不超过42000元,问最少进货甲种空气净化器多少台?
18.(8分)(1)计算:![]() . (2)解方程:(x+2)2=1.
. (2)解方程:(x+2)2=1.
19.(8分)如图,在四边形ABCD中,∠D=90°,AB=13,BC=12,CD=4,AD=3.
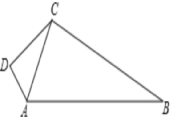
求:(1)AC的长度;
(2)判断△ACB是什么三角形?并说明理由?
(3)四边形ABCD的面积。
20.(8分)提出问题:
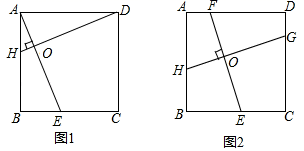
(1)如图1,在正方形ABCD中,点E,H分别在BC,AB上,若AE⊥DH于点O,求证:AE=DH;
类比探究:
(2)如图2,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上,若EF⊥HG于点O,探究线段EF与HG的数量关系,并说明理由.
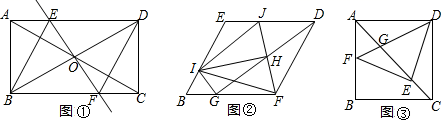
21.(8分) (1)如图①,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,交AD于点E,交BC于点F,连接BE、DF,且BE平分∠ABD.
①求证:四边形BFDE是菱形;
②直接写出∠EBF的度数;
(2)把(1)中菱形BFDE进行分离研究,如图②,点G、I分别在BF、BE边上,且BG=BI,连接GD,H为GD的中点,连接FH并延长,交ED于点J,连接IJ、IH、IF、IG.试探究线段IH与FH之间满足的关系,并说明理由;
(3)把(1)中矩形ABCD进行特殊化探究,如图③,当矩形ABCD满足AB=AD时,点E是对角线AC上一点,连接DE、EF、DF,使△DEF是等腰直角三角形,DF交AC于点G.请直接写出线段AG、GE、EC三者之间满足的数量关系.
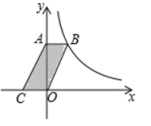
22.(10分)如图,平行四边形![]() 的顶点
的顶点![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,顶点
轴上,顶点![]() 在反比例函数
在反比例函数![]() 的图象上,求平行四边形
的图象上,求平行四边形![]() 的面积.
的面积.
23.(10分)因式分解:
(1)36﹣x2
(2)ma2﹣2ma+m
24.(12分)已知方程组![]() 的解中,x为非正数,y为负数.
的解中,x为非正数,y为负数.
(1)求a的取值范围;
(2)化简|a﹣3|+|a+2|.
参考答案
一、选择题(每小题3分,共30分)
1、B
2、A
3、D
4、A
5、A
6、B
7、C
8、A
9、D
10、A
二、填空题(本大题共有6小题,每小题3分,共18分)
11、1
12、![]()
13、①②④.
14、x<-1
15、![]()
16、1
三、解下列各题(本大题共8小题,共72分)
17、(1)每台甲种空气净化器、每台乙种空气净化器的进价分别为1200元,1500元(2)至少进货甲种空气净化器10台.
18、 (1)![]() (2)x1=1,x2=-2
(2)x1=1,x2=-2
19、(1)5(2)直角三角形,理由见解析(3)36
20、(1)见解析;(2)EF=GH,理由见解析
21、(1)①详见解析;②60°.(1)IH=![]() FH;(3)EG1=AG1+CE1.
FH;(3)EG1=AG1+CE1.
22、3
23、(1)(6+x)(6﹣x);(1)m(a﹣1)1.
24、(1)﹣2<a≤3;(2)1
浙江省绍兴市阳明中学2023-2024学年数学九上期末监测模拟试题含答案: 这是一份浙江省绍兴市阳明中学2023-2024学年数学九上期末监测模拟试题含答案,共8页。试卷主要包含了如图,⊙中,,则等于等内容,欢迎下载使用。
浙江省绍兴市暨阳2023-2024学年八上数学期末学业质量监测模拟试题含答案: 这是一份浙江省绍兴市暨阳2023-2024学年八上数学期末学业质量监测模拟试题含答案,共7页。试卷主要包含了答题时请按要求用笔,下列条件中能作出唯一三角形的是,要使分式无意义,则的取值范围是等内容,欢迎下载使用。
浙江省绍兴市名校2023-2024学年数学八上期末质量跟踪监视模拟试题含答案: 这是一份浙江省绍兴市名校2023-2024学年数学八上期末质量跟踪监视模拟试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,下列关于一次函数,把通分,下列计算正确的是,如图等内容,欢迎下载使用。












