人教版九年级上册22.1.4 二次函数y＝ax2＋bx＋c的图象和性质第2课时教学设计

第二十二章 二次函数

22.1 二次函数的图象和性质

22.1.4 二次函数y=ax2+bx+c的图象和性质

第2课时  用待定系数法求二次函数的解析式

一、教学目标

1.会用待定系数法求二次函数的表达式.(难点）

2.会根据待定系数法解决关于二次函数的相关问题.（重点）

二、教学重难点

重点：根据待定系数法解决关于二次函数的相关问题.

难点：用待定系数法求二次函数的表达式.

三、教学过程

【新课导入】

[复习导入]1.一次函数y=kx+b(k≠0)有几个待定系数？通常需要几个点的坐标求出它的表达式？

2.求一次函数表达式的方法是什么？它的一般步骤是什么？

(1)设：（表达式）

(2)代：（坐标代入）

待定系数法                        (3)解：方程（组）

(4)           还原：（写表达式）

[思考]二次函数y=ax2+bx+c(a≠0)中有几个待定系数？需要几个抛物线上的点的坐标才能求出来？

[思考]已知一个二次函数的图象经过（-3，0），（-1，0），（0，-3）三点，求此二次函数的解析式.

解：设这个二次函数的表达式是y=ax2+bx+c,把（-3，0），（-1，0），（0，-3）代入y=ax2+bx+c得                    

9a-3b+c=0，                      a=-1，

 a+b+c=0，                       b=-4，

c=-3，       解得                c=-3.

∴所求的二次函数的表达式是y=-x2-4x-3.

[归纳总结]一般式法求二次函数表达式的方法

其步骤是：

①设函数表达式为y=ax2+bx+c；

②代入后得到一个三元一次方程组；

③解方程组得到a，b，c的值；

④把待定系数用数字换掉，写出函数表达式.

[思考]已知二次函数的图象经过点A（3，0），B（2，-3），C（0，-3），求函数的表达式.

解：设函数表达式为y=ax2+bx+c，由题意得

      9a+3b+c=0，                 a=1，

      4a+2b+c=-3，                b=-2，

      c=-3.           解得        c=-3.

所求函数的表达式为y=x2-2x-3.

[思考]已知抛物线的顶点坐标为M（1，－2），且经过点N（2，3），求此二次函数的解析式.

[分析]因为抛物线的顶点坐标为M（1，－2），所以设此二次函数的解析式为y＝

a（x－1）2－2，把点N（2，3）代入解析式解答.

解：已知抛物线的顶点坐标为M（1，－2），

   设此二次函数的解析式为y＝a（x－1）2－2，

   把点N（2，3）代入解析式，得a－2＝3，即a＝5，

   ∴此函数的解析式为y＝5（x－1）2－2.

[归纳总结]顶点式法求二次函数解析式的步骤：

①设函数解析式是y=a（x-h）2+k；

②先代入顶点坐标，得到关于a的一元一次方程；

③将另一点的坐标代入原方程求出a值；

④把a用数值换掉，写出函数解析式.

若题目给出了二次函数的顶点坐标，则采用顶点式求解简单.

[思考]一个二次函数的图象经点 (0，1)，它的顶点坐标为(8，9)，求这个二次函数的表达式.

解：因为这个二次函数的图象的顶点坐标为(8，9)，因此，可以设函数表达式为

                   y=a(x-8)2+9.

又由于它的图象经过点(0，1)，可得    0=a(0-8)2+9. 

 解得    a= -  .

∴所求的二次函数的解析式是y= - （x-8）2 +9.

[思考]已知抛物线经过两点A（1，0），B（0，－3）， C（3，0），求此二次函数的解析式。

[分析]可设交点式y＝a（x－1）（x－3），然后把B点坐标代入求出a即可；

解：由题意得，抛物线与x轴交于A（1，0）， C（3，0）两点

        设抛物线解析式为  y＝a（x－1）（x－3），

        把B（0，－3）代入得：a（－1）×（－3）＝－3，解得a＝－1，

     ∴抛物线解析式为y＝－（x－1）（x－3）＝－x2＋4x－3。

[归纳总结]交点式法求二次函数解析式的步骤：

①设函数解析式是y=a（x-x1）（x-x2）；

②先把两交点的横坐标x1，x2代入到解析式中，得到关于a的一元一次方程；

③将另一点的坐标代入原方程求出a的值；

④a用数值换掉，写出函数解析式.

已知抛物线与x轴的两个交点，则采用交点式求解简单.

[思考]已知抛物线与x轴相交于点A(－1，0)，B(1，0)，且过点M(0，1)，

求此函数的表达式．

解：∵点A(－1，0)，B(1，0)是图象与x轴的交点，

         ∴设二次函数的表达式为y＝a(x＋1)(x－1)．

          又抛物线过点M(0，1)，

          可得1＝a(0＋1)(0－1)，解得a＝－1，

          所以所求抛物线的表达式为y＝－(x＋1)(x－1)，即y＝－x2＋1.

【课堂小结】

【课堂训练】

1. 已知二次函数的图象与y轴交点的纵坐标为1，且经过点（2，5）和（-2，13），求这个二次函数的表达式.

解：因为二次函数图象与y轴交点的纵坐标为1，所以c=1.

设二次函数的表达式为y＝ax2＋bx＋1，

将点（2，5）和（-2，13）代入y＝ax2＋bx＋1，得

    5=4a+2b+1               a=2

13=4a-2b+1      解得    b=-2

所以所求二次函数的表达式为y＝2x2-2x＋1.

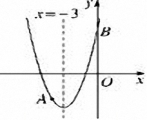
2. 如图，抛物线y＝x2＋bx＋c过点A(－4，－3)，与y轴交于点B，对称轴是x＝－3，请解答下列问题：

（1）求抛物线的表达式；

（2）若和x轴平行的直线与抛物线交于C，D两点，点C在对称轴左侧，且CD＝8，求△BCD的面积．

解：(1)把点A(－4，－3)代入y＝x2＋bx＋c

得16－4b＋c＝－3，c－4b＝－19.

∵对称轴是x＝－3，∴   - ＝－3，

∴b＝6，∴c＝5，

∴抛物线的表达式是y＝x2＋6x＋5；

(2)∵CD∥x轴，∴点C与点D关于x＝－3对称．

∵点C在对称轴左侧，且CD＝8，

∴点C的横坐标为－7，

∴点C的纵坐标为(－7)2＋6×(－7)＋5＝12.

∵点B的坐标为(0，5)，

∴△BCD中CD边上的高为12－5＝7，

∴△BCD的面积＝ ×8×7＝28.

中考链接

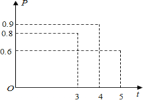
1. （2020•长沙）“闻起来臭，吃起来香”的臭豆腐是长沙特色小吃，臭豆腐虽小，但制作流程却比较复杂，其中在进行加工煎炸臭豆腐时，我们把“焦脆而不糊”的豆腐块数的百分比称为“可食用率”．在特定条件下，“可食用率”P与加工煎炸时间t（单位：分钟）近似满足的函数关系为：P＝at2+bt+c（a≠0，a，b，c是常数），如图记录了三次实验的数据．

根据上述函数关系和实验数据，可以得到加工煎炸臭豆腐的最佳时间为（  C  ）

A．3.50分钟    B．4.05分钟      C．3.75分钟     D．4.25分钟

2.（2020•兰州）点A（﹣4，3），B（0，k）在二次函数y＝﹣（x+2）2+h的图象上，则k＝3．

3.（2020•温州）已知抛物线y＝ax2+bx+1经过点（1，﹣2），（﹣2，13）．

（1）求a，b的值．

（2）若（5，y1），（m，y2）是抛物线上不同的两点，且y2＝12﹣y1，求m．

解：（1）把点（1，﹣2），（﹣2，13）代入y＝ax2+bx+1得，

      -2=a+b+1                     a=1

  13=4a-2b+1           解得：  b=-4

（2）由（1）得函数解析式为y＝x2﹣4x+1，

把x＝5代入y＝x2﹣4x+1得，y1＝6，

∴y2＝12﹣y1＝6，

∵y1＝y2，且对称轴为直线x＝2，

∴m＝4﹣5＝﹣1．

【布置作业】

【教学反思】

求函数解析式是初中数学主要内容之一，求二次函数的解析式也是联系高中数学的重要纽带．求函数的解析式，应恰当地选用函数解析式的形式，选择得当，解题简捷，若选择不当，解题繁琐．