初中数学22.1.3 二次函数y＝a（x－h）2＋k的图象和性质第3课时教学设计

这是一份初中数学22.1.3 二次函数y＝a（x－h）2＋k的图象和性质第3课时教学设计，共5页。教案主要包含了教学目标，教学重难点，教学过程等内容，欢迎下载使用。
第3课时二次函数y=a(x-h)2+k的图象和性质一、教学目标1．会画二次函数y=a(x-h)2+k (a ≠0)的图象.2．掌握二次函数y=a(x-h)2+k (a≠0)图象的性质，会灵活应用其性质.3. 理解二次函数y=a(x-h)2+k (a≠0)与y=ax2之间的联系.二、教学重难点重点：掌握二次函数y=a(x-h)2+k (a≠0)图象的性质，会灵活应用其性质.难点：掌握二次函数y=a(x-h)2的性质并会应用并会应用，理解理解二次函数y=a(x-h)2+k (a≠0)与y=ax2之间的联系．三、教学过程【新课导入】[复习导入]说出下列函数图象的开口方向,对称轴,顶点,最值和增减变化情况:
(1)y=ax2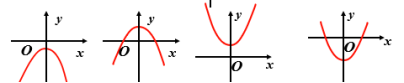  
(2)y=ax2+k(3)y=a(x-h)2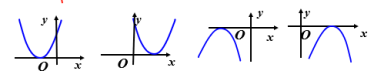   【新知探究】（一）二次函数y=a（x-h）2+k的图象和性质例1 画出函数的图像.指出它的开口方向、对称轴和顶点.解:  先列表x…-4-3-2-1012……-5.5-3-1.5-1-1.5-3-5.5…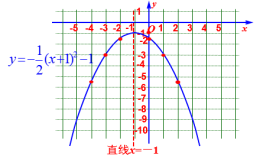再描点、连线开口方：向向下；对称轴：直线x=-1;顶点坐标：(-1,-1)   [思考]试一试画出函数y=2(x+1)2-2图象，并说出抛物线的开口方向、对称轴、顶点.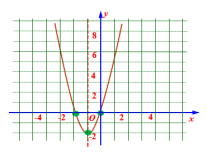开口方向：向下；对称轴：直线x=-1;顶点坐标：(-1,-2)   [归纳总结]二次函数y=a(x-h)2+k（a ≠ 0）的性质y=a(x-h)2+ka>0a<0开口方向向上向下对称轴直线x=h直线x=h顶点坐标（h,k） （h,k）最值当x=h时，y最小值= k当x=h时，y最大值= k增减性当x<h时，y随着x的增大而减小；当x>h时，y随着x的增大而增大.当x<h时,y随着x的增大而增大；当x>h时，y随着x的增大而减小.（二）二次函数y=a(x-h)2+k (a≠0)与y=ax2之间的联系[思考]怎样移动抛物线 就可以得抛物线抛？[课件展示]平移方法1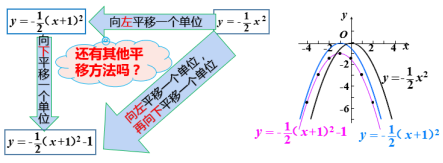[思考]怎样移动抛物线 就可以得抛物线抛？[课件展示]平移方法2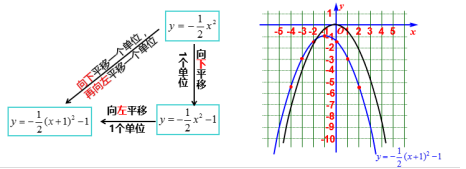 [交流讨论]二次函数y=a(x-h)2+k 与y=ax2的关系可以看作互相平移得到的温馨提示：1.上下平移，括号外上加下减；2.左右平移，括号内左加右减.3.二次项系数a不变. 概括为：左加右减，上加下减.[归纳总结]一般地，抛物线与形状相同，位置不同，把抛物线y=ax2向上（下）向左（右）平移，可以得到抛物线y=a(x－h)2+k平移的方向、距离要根据h，k的值来决定．抛物线有如下特点：（1）当a>0时，开口向上；当a<0时，开口向下；（2）对称轴是直线x=h；（3）顶点坐标是（h, k).[归纳总结]二次函数y=a(x-h)2+k 的图象与性质y=a(x-h)2+ka>0a<0函数图象h>0h<0开口方向向上向下对称轴直线x=h直线x=h顶点坐标（h,k） （h,k）函数的增减性当x<h时，y随着x的增大而减小；当x>h时，y随着x的增大而增大.当x<h时,y随着x的增大而增大；当x>h时，y随着x的增大而减小.最值当x=h时，y最小值= k当x=h时，y最大值= k 



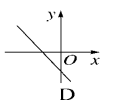
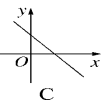
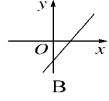
例1 已知二次函数y＝a(x－1)2－c的图象如图所示，则一次函数y＝ax＋c的大致图象可能是(　A　)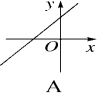
例2   要修建一个圆形喷水池,在池中心竖直安装一根水管.在水管的顶端安装一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管应多长?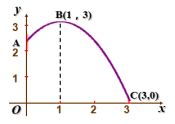解:如图建立直角坐标系,点(1,3)是图中这段抛物线的顶点.因此可设这段抛物线对应的函数是y=a(x－1)2＋3 (0≤x≤3).∵这段抛物线经过点(3,0)，∴  0=a(3－1)2＋3.解得:因此y=(x－1)2＋3 (0≤x≤3).当x=0时,y=2.25.答:水管长应为2.25m.【课堂小结】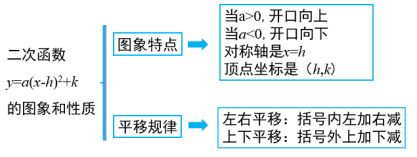【课堂训练】1.抛物线y=-3(x+2)2-4的顶点坐标是（-2，-4），当x≤-2 时，函数值y随x的增大而增大. 2.若抛物线的对称轴为x =-1，与x轴的一个交点坐标为（1,0），则这条抛物线与x轴的另一个交点是（-3，0）.3．（2020•宿迁）将二次函数y＝（x﹣1）2+2的图象向上平移3个单位长度，得到的拋物线相应的函数表达式为（　D　）A．y＝（x+2）2﹣2 B．y＝（x﹣4）2+2 C．y＝（x﹣1）2﹣1 D．y＝（x﹣1）2+54. 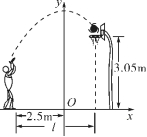小明在某次投篮中，篮球的运动线路是抛物线y=x2+3.5的一部分(如图)，若球正好命中篮圈中心，则他与篮底的距离l是(B )A.  3.5 mB.  4 mC.  4.5 mD.  4.6 m5.抛物线y = 4(x－3)2＋7可以由抛物线y=4x2怎样平移得到?由抛物线向上平移7个单位再向右平移3个单位得到的. 6.如果一条抛物线的形状与的形状相同，且顶点坐标是（4，-2），试求这个函数关系式. 【布置作业】【教学反思】教学过程中，强调学生自主探索和合作交流，在操作中探究二次函数y＝a(x－h)2＋k的图象与性质，体会数学建模的数形结合思想方法..