初中数学人教版九年级上册第二十三章 旋转23.2 中心对称23.2.1 中心对称课时练习
展开![]() 23.2 中心对称
23.2 中心对称
【学习目标】
1.理解两个图形关于某一点中心对称的概念及其性质,能作一个图形关于某一个点的中心对称图形.
2.理解中心对称图形.
3.能熟练掌握关于原点对称的点的坐标.
4.能综合运用平移、轴对称、旋转等变换解决图形变换问题.
【学习重难点】
重点:中心对称性质的应用
难点:旋转中的截长补短方法。
知识点一:中心对称及其相关概念
中心对称的定义
把一个图形绕着某个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心,这两个图形中的对应点叫做关于中心的对称点.
例题.下列四张扑克牌图案,属于中心对称的是( )
A. B.
B. C.
C. D.
D.
变式1.下列英语单词中,是中心对称图形的是( )
A.SOS B.CEO C.MBA D.SAR
变式2.下列四组图形中,左边的图形与右边的图形成中心对称的有( )
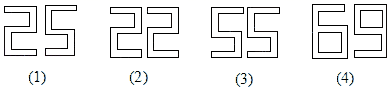
A.1组 B.2组 C.3组 D.4组
知识点二:中心对称的性质
(2)中心对称的性质
①关于中心对称的两个图形能够完全重合;
②关于中心对称的两个图形,对应点的连线都经过对称中心,并且被对称中心平分.
例题.已知△ABC和△DEF关于点O对称,相应的对称点如图所示,则下列结论正确的是( )
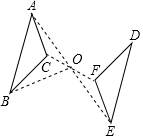
A.AO=BO B.BO=EO
C.点A关于点O的对称点是点D D.点D 在BO的延长线上
变式1.成中心对称的两个图形,下列说法正确的是( )
①一定形状相同;②大小可能不等;③对称中心必在图形上;④对称中心可能只在一个图形上;⑤对称中心必在对应点的连线上.
A.①③ B.③④ C.④⑤ D.①⑤
变式2.如图,在平面直角坐标系中,若△ABC与△A1B1C1关于E点成中心对称,则对称中心E点的坐标是( )
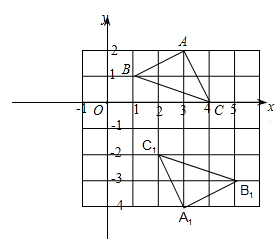
A.(3,﹣1) B.(0,0) C.(2,﹣1) D.(﹣1,3)
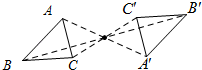
变式3.如图,△ABC与△A′B′C′关于点O成中心对称,∠ABC=45°,∠B′C′A′=80°,∠BAC= 55 °.
知识点三:中心对称的作图方法
(1)旋转图形的作法:
根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.
(2)旋转作图有自己独特的特点,决定图形位置的因素较多,旋转角度、旋转方向、旋转中心,任意不同,位置就不同,但得到的图形全等.
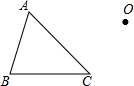
例题.如图,作出△ABC绕点O逆时针方向旋转90°的图形.
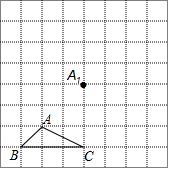
变式1.如图,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A按逆时针方向旋转90°,得到△A1B2C2,在网格中画出旋转后的△A1B2C2.
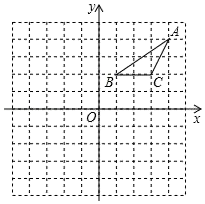
变式2在正方形网格中建立如图所示的平面直角坐标系xOy.△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题:
(1)将△ABC向下平移5个单位长度,画出平移后的A1B1C1,并写出点A的对应点A1的坐标;
(2)画出△A1B1C1关于y轴对称的△A2B2C2;
(3)将△ABC绕点C逆时针旋转90°,画出旋转后的△A3B3C.
知识点四:中心对称图形
(1)定义
把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心.
注意:中心对称图形和中心对称不同,中心对称是两个图形之间的关系,而中心对称图形是指一个图形自身的特点,这点应注意区分,它们性质相同,应用方法相同.
(2)常见的中心对称图形
平行四边形、圆形、正方形、长方形等等.
知识点五:关于远点对称的点的坐标
例题.下列图形中,既是轴对称图形又是中心对称图形的是( )
A.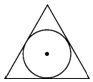 B.
B.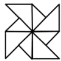 C.
C.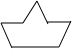 D.
D.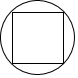
变式1.下列图形中,既是中心对称图形,又是轴对称图形的是( )
A. B.
B.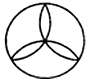 C.
C.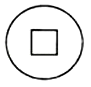 D.
D.
变式2.下列图形中,①等腰三角形;②平行四边形;③等腰梯形;④圆;⑤正六边形;⑥菱形;⑦正五边形,是中心对称图形的有 (填序号)
拓展点一:中心对称图形与轴对称图形的综合辨析问题
例题.如图所示的图案中,是轴对称图形而不是中心对称图形的个数是( )
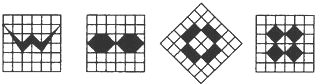
A.4个 B.3个 C.2个 D.1个
变式1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
B. C.
C. D.
D.
变式2.如图,点A,B在方格纸的格点上,将线段AB先向右平移3格,再向下平移2个单位,得线段DC,点A的对应点为D,连接AD、BC,则关于四边形ABCD的对称性,下列说法正确的是( )
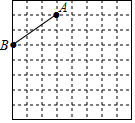
A.既是轴对称图形,又是中心对称图形
B.是中心对称图形,但不是轴对称图形
C.是轴对称图形,但不是中心对称图形
D.既不是轴对称图形,也不是中心对称图形
拓展点二:中心对称和中心对称图形的性质和应用
例题.如图,点A,B,C的坐标分别为(2,5),(6,3),(4,﹣1);若以点A,B,C,D为顶点的四边形既是轴对称图形,又是中心对称图形,则点D的坐标可能是( )
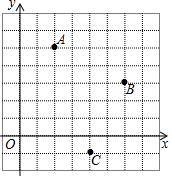
A.(0,0) B.(0,1) C.(3,2) D.(1,0)
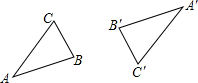
变式1.如图,已知△ABC与△A′B′C′成中心对称图形,求出它的对称中心O.
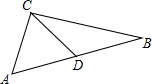
变式2.如图,在△ABC中,点D是AB边上的中点,已知AC=4,BC=6,
(1)画出△BCD关于点D的中心对称图形;
(2)根据图形说明线段CD长的取值范围.
拓展点三:关于原点对称的点的坐标特征
例题.在平面直角坐标系中,点P(﹣3,﹣5)关于原点对称的点的坐标是( )
A.(3,﹣5) B.(﹣3,5) C.(3,5) D.(﹣3,﹣5)
变式1.在平面直角坐标系中,P点关于原点的对称点为P1(﹣3,﹣![]() ),P点关于x轴的对称点为P2(a,b),则
),P点关于x轴的对称点为P2(a,b),则![]() =( )
=( )
A.﹣2 B.2 C.4 D.﹣4
变式2.在平面直角坐标系中,已知点A(2a﹣b,﹣8)与点B(﹣2,a+3b)关于原点对称,求a、b的值.
拓展点四:平移、轴对称、中心对称的综合作图题
1.如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣4,3),B(﹣3,1),C(﹣1,3).
(1)请按下列要求画图:
①平移△ABC,使点A的对应点A1的坐标为(﹣4,﹣3),请画出平移后的△A1B1C1;
②△A2B2C2与△ABC关于原点O中心对称,画出△A2B2C2.
(2)若将△A1B1C1绕点M旋转可得到△A2B2C2,请直接写出旋转中心M点的坐标 .
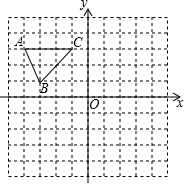
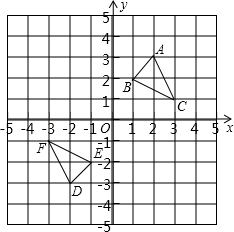
2.如图,三角形DEF是三角形ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点P(a+3b,4a﹣b)与点Q(2a﹣9,2b﹣9)也是通过上述变换得到的对应点,求a,b的值.
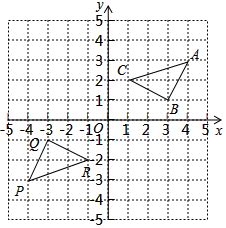
3.如图,三角形PQR是三角形ABC经过某种变换后得到的图形,分别观察点A与点P,点B与点Q,点C与点R的坐标之间的关系.
(1)若三角形ABC内任意一点M的坐标为(x,y),点M经过这种变换后得到点N,根据你的发现,点N的坐标为 .
(2)若三角形PQR先向上平移3个单位,再向右平移4个单位得到三角形P′Q′R′,画出三角形P′Q′R′并求三角形P′AC的面积.
(3)直接写出AC与y轴交点的坐标 .
人教版九年级上册23.2.1 中心对称优秀课时练习: 这是一份人教版九年级上册23.2.1 中心对称优秀课时练习,共12页。试卷主要包含了2 中心对称》分层练习,在下列几何图形中等内容,欢迎下载使用。
数学第二十三章 旋转23.2 中心对称23.2.1 中心对称优秀课后复习题: 这是一份数学第二十三章 旋转23.2 中心对称23.2.1 中心对称优秀课后复习题,共9页。试卷主要包含了2 中心对称》同步精炼等内容,欢迎下载使用。
初中人教版23.2.1 中心对称复习练习题: 这是一份初中人教版23.2.1 中心对称复习练习题,文件包含232中心对称练习学生版docx、232中心对称练习教师版docx等2份试卷配套教学资源,其中试卷共27页, 欢迎下载使用。