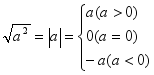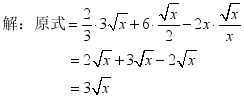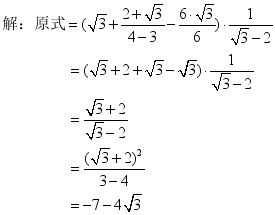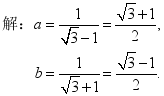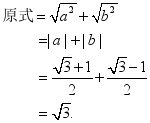沪教版 (五四制)八年级上册16．1 二次根式获奖表格教案及反思

课  题

十六章二次根式

课 型

复习

教 时

1

教  学

目  标

1.理解二次根式、最简二次根式、同类二次根式、分母有理化等概念的意义。

2.掌握二次根式的性质，并能运用二次根式性质进行二次根式的运算。

重  点

二次根式有关性质的灵活应用，二次根式的正确运算。

难  点

二次根式有关性质的灵活应用，二次根式的正确运算。

教具准备

多媒体课件

教   学   过   程

教师活动

学生活动

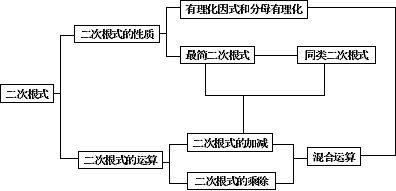
一、建立知识结构：

今天主要复习二次根式，请问在本章中我们主要学习了关于二次根式的哪些知识？

教师帮助建立知识结构：

复习各知识点，并板书二次根式概念和性质：

1．二次根式概念：代数式叫做二次根式.

2．二次根式性质：

(1)；

(2)；

(3)；

(4).

二、知识运用：

例题1  填空题：

1．成立的条件是____________.

问：如何思考？

答案：.

小结：由于的结果一定非负，所以，此题可直接得到不等式求解.

2．成立的条件是___________.

问：如何思考？

答案：.

小结：求二次根式成立的条件，应考虑被开方数非负，分母不为零等条件，将问题转化为方程（组）、不等式（组）求解.

3．在、、、、、、中最简二次根式有_____________________.

问1：上式中哪些是最简二次根式？将其余根式化为最简二次根式.

小结：最简二次根式必须满足：

被开方数中（1）各因式指数为1；

（2）不含分母.

问2：以上是否有同类二次根式？

小结：同类二次根式的前提是最简二次根式，条件是被开方数相同.

问3：若已知最简二次根式与是同类二次根式，如何确定m的值？

追问：所求出的m的值都对吗？

小结：字母的取值要使被开方数大于或等于零。

4、计算：

例题2   计算：

(1)

(2)

.

(3)

问：第一个括号内的计算应如何进行？

问：说出的有理化因式？

小结：1、二次根式的混合运算先确定运算顺序；2、结果要化为最简二次根式.

例题3  解不等式：

问1：如何求解？

问2：在化系数为1时应注意什么？

问3：请比较与4的大小.

解：

小结：解含无理数系数的一元一次不等式步骤不变，注意当不等式两边同除以负数时，不等号的方向要改变.

例题4  已知：

求的值.

小结：在较为复杂的求代数式值的运算中，通常应先化简再求值.

三、课堂小结：

本节课主要学习了什么？

四、回家作业：

一张练习卷.

思考、回顾、复习旧知。

复习二次根式的概念和性质。

例题采取讲练结合的形式，由师生共同完成

谈收获和注意点

举例板书设计：

1.二次根式的概念、性质

2.例题解题格式

课后反思：