


山西省吕梁市兴县康宁中学2022-2023学年数学七年级第二学期期末考试模拟试题含答案
展开山西省吕梁市兴县康宁中学2022-2023学年数学七年级第二学期期末考试模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生须知:
1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题(每小题3分,共30分)
1.二次函数y=ax1+bx+c(a≠0)的图象如图所示,有下列结论:①abc>0;②1a+b=0;③若m为任意实数,则a+b>am1+bm;④a﹣b+c>0;⑤若ax11+bx1=ax11+bx1,且x1≠x1,则x1+x1=1.其中,正确结论的个数为( )
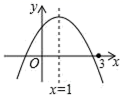
A.1 B.1 C.3 D.4
2.某经销商销售一批多功能手表,第一个月以200元/块的价格售出80块,第二个月起降价,以150元/块的价格将这批手表全部售出,销售总额超过了2.7万元,则这批手表至少有( )
A.152块 B.153块 C.154块 D.155块
3.下列根式中与![]() 是同类二次根式的是( ).
是同类二次根式的是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.一直尺与一个锐角为![]() 角的三角板如图摆放,若
角的三角板如图摆放,若![]() ,则
,则![]() 的度数为( )
的度数为( )
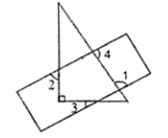
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.点A,B,C,D都在如图所示的由正方形组成的网格图中,且线段CD与线段AB成位似图形,则位似中心为( )
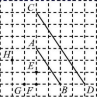
A.点E B.点F
C.点H D.点G
6.如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 、
、![]() 两点,且点
两点,且点![]() 的坐标为
的坐标为![]() ,将直线
,将直线![]() 向上平移
向上平移![]() 个单位,交双曲线
个单位,交双曲线![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,且
,且![]() 的面积是
的面积是![]() .给出以下结论:(1)
.给出以下结论:(1)![]() ;(2)点
;(2)点![]() 的坐标是
的坐标是![]() ;(3)
;(3)![]() ;(4)
;(4)![]() .其中正确的结论有
.其中正确的结论有![]()
![]()
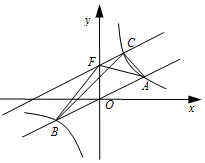
A.1个 B.2个 C.3个 D.4个
7.计算![]() 的结果是( )
的结果是( )
A.-2 B.2 C.-4 D.4
8.在下列四个函数中,是一次函数的是( )
A.y![]() B.y=x2+1 C.y=2x+1 D.y
B.y=x2+1 C.y=2x+1 D.y![]() +6
+6
9.如图,表示A点的位置,正确的是( )
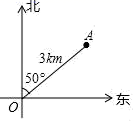
A.距O点3km的地方
B.在O点的东北方向上
C.在O点东偏北40°的方向
D.在O点北偏东50°方向,距O点3km的地方
10.绍兴市著名的桥乡,如图,石拱桥的桥顶到水面的距离CD为8m,桥拱半径OC为5m,则水面宽AB为( )

A.4m B.5m C.6m D.8m
二、填空题(本大题共有6小题,每小题3分,共18分)
11.若2x﹣5没有平方根,则x的取值范围为_____.
12.点D、E、F分别是△ABC三边的中点,若△ABC的周长是16,则△DEF的周长是_____.
13.颖颖同学用20元钱去买方便面35包,甲种方便面每包0.7元,乙种方便面每包0.5元,则她最多可买甲种方便面_____包.
14.若关于x的一元二次方程![]() x2﹣2kx+1-4k=0有两个相等的实数根,则代数式(k-2)2+2k(1-k)的值为______.
x2﹣2kx+1-4k=0有两个相等的实数根,则代数式(k-2)2+2k(1-k)的值为______.
15.如果![]() 的平方根是
的平方根是![]() ,则
,则![]() _________
_________
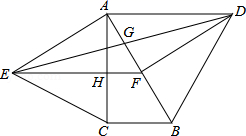
16.如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=![]() BD
BD
其中正确结论的为______(请将所有正确的序号都填上).
三、解下列各题(本大题共8小题,共72分)
17.(8分)孝感市委市政府为了贯彻落实国家的“精准扶贫”战略部署,组织相关企业开展扶贫工作,博大公司为此制定了关于帮扶A、B两贫困村的计划.今年3月份决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗.已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如表:
目的地 费用 车型 | A村(元/辆) | B村(元/辆) |
大货车 | 800 | 900 |
小货车 | 400 | 600 |
(1)求这15辆车中大小货车各多少辆?
(2)现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A、B两村总运费为y元;
①试求出y与x的函数解析式;
②若运往A村的鱼苗不少于108箱,请你写出使总运费最少的货车调配方案,并求出最少运费.
18.(8分)如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒
方向以每秒![]() 个单位长的速度向
个单位长的速度向![]() 点匀速运动,同时点
点匀速运动,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒
方向以每秒![]() 个单位长的速度向点
个单位长的速度向点![]() 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点
匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点![]() 、
、![]() 运动的时间是
运动的时间是![]() 秒(
秒(![]() ).过点
).过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .
.
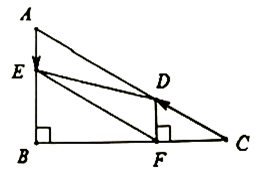
(1)![]() 的长是 ,
的长是 ,![]() 的长是 ;
的长是 ;
(2)在![]() 、
、![]() 的运动过程中,线段
的运动过程中,线段![]() 与
与![]() 的关系是否发生变化?若不变化,那么线段
的关系是否发生变化?若不变化,那么线段![]() 与
与![]() 是何关系,并给予证明;若变化,请说明理由.
是何关系,并给予证明;若变化,请说明理由.
(3)四边形![]() 能够成为菱形吗?如果能,求出相应的
能够成为菱形吗?如果能,求出相应的![]() 值;如果不能,说明理由.
值;如果不能,说明理由.
19.(8分)某制笔企业欲将200件产品运往![]() ,
,![]() ,
,![]() 三地销售,要求运往
三地销售,要求运往![]() 地的件数是运往
地的件数是运往![]() 地件数的2倍,各地的运费如图所示.设安排
地件数的2倍,各地的运费如图所示.设安排![]() 件产品运往
件产品运往![]() 地.
地.
|
|
|
|
产品件数(件) |
|
|
|
运费(元) |
|
|
|
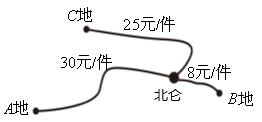
(1)①根据信息补全上表空格.②若设总运费为![]() 元,写出
元,写出![]() 关于
关于![]() 的函数关系式及自变量的取值范围.
的函数关系式及自变量的取值范围.
(2)若运往![]() 地的产品数量不超过运往
地的产品数量不超过运往![]() 地的数量,应怎样安排
地的数量,应怎样安排![]() ,
,![]() ,
,![]() 三地的运送数量才能达到运费最少.
三地的运送数量才能达到运费最少.
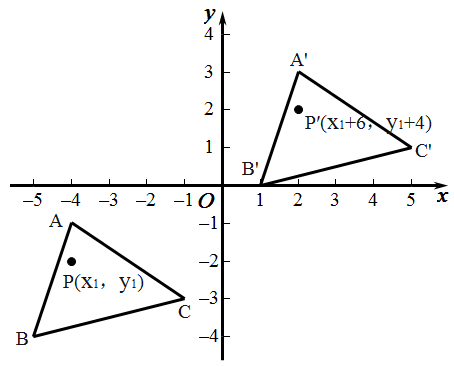
20.(8分)如图所示,△A′B′C′是△ABC经过平移得到的,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4).
(1)请写出三角形ABC平移的过程;
(2)分别写出点A′,B′,C′ 的坐标.
(3)求△A′B′C′的面积.
21.(8分)为了进一步了解某校八年级学生的身体素质情况,体育老师对该校八年级(1)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,图表如下所示:
组别 | 次数x | 频数(人数) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 | a |
第4组 | 140≤x<160 | 18 |
第5组 | 160≤x<180 | 6 |
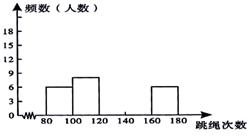
请结合图表完成下列问题:
(1)求表中a的值并把频数分布直方图补充完整;
(2)该班学生跳绳的中位数落在第 组,众数落在第 组;
(3)若在一分钟内跳绳次数少于120次的为测试不合格,则该校八年级共1000人中,一分钟跳绳 不合格的人数大约有多少?
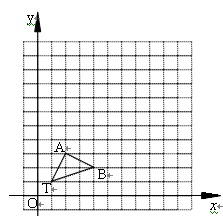
22.(10分)如图,在12×12的正方形网格中,△TAB 的顶点坐标分别为T(1,1)、A(2,3)、B(4,2).
(1)以点T(1,1)为位似中心,按比例尺(TA′∶TA)3∶1在位似中心的同侧将△TAB放大为△TA′B′,放大后点A、B的对应点分别为A′、B′.画出△TA′B′,并写出点A′、B′的坐标;
(2)在(1)中,若C(a,b)为线段AB上任一点,写出变化后点C的对应点C′的坐标.
23.(10分)今年水果大丰收,A,B两个水果基地分别收获水果380件、320件,现需把这些水果全部运往甲、乙两销售点,从A基地运往甲、乙两销售点的费用分别为每件40元和20元,从B基地运往甲、乙两销售点的费用分别为每件15元和30元,现甲销售点需要水果400件,乙销售点需要水果300件.
(1)设从A基地运往甲销售点水果x件,总运费为W元,请用含x的代数式表示W,并写出x的取值范围;
(2)若总运费不超过18300元,且A地运往甲销售点的水果不低于200件,试确定运费最低的运输方案,并求出最低运费.
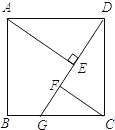
24.(12分)如图,四边形ABCD是正方形,G是BC上任意一点(点G与B、C不重合),AE⊥DG于E,CF∥AE交DG于F.请你经过观察、猜测线段FC、AE、EF之间是否存在一定的数量关系?若存在,证明你的结论;若不存在,请说明理由.
参考答案
一、选择题(每小题3分,共30分)
1、B
2、C
3、C
4、C
5、B
6、C
7、B
8、C
9、D
10、D
二、填空题(本大题共有6小题,每小题3分,共18分)
11、x<![]() .
.
12、1.
13、1
14、![]()
15、81
16、①③④
三、解下列各题(本大题共8小题,共72分)
17、(1)这15辆车中大货车用8辆,小货车用7辆;(2)①y=100x+9400(3≤x≤8,且x为整数);②使总运费最少的调配方案是:7辆大货车、3辆小货车前往A村;1辆大货车、4辆小货车前往B村.最少运费为10100元.
18、(1)![]() ,
,![]() ;(2)
;(2)![]() 与
与![]() 平行且相等;(3)当
平行且相等;(3)当![]() 时,四边形
时,四边形![]() 为菱形
为菱形
19、(1)①见解析;②![]() ,
,![]() ;(2)安排运往
;(2)安排运往![]() ,
,![]() ,
,![]() 三地的产品件数分别为40件、80件,80件时,运费最少.
三地的产品件数分别为40件、80件,80件时,运费最少.
20、(1)见解析;(2)A′(2,3) B′(1,0) C′(5,1);(3)5.5
21、(1)a=12,(2)3;4;(3)280(人)
22、(1)A′坐标为(4,7),B′坐标为(10,4);(2)点C′的坐标为(3a-2,3b-2 ) .
23、(1)W=35x+11200,x的取值范围是80≤x≤380;(2)从A基地运往甲销售点的水果200件,运往乙销售点的水果180件,从B基地运往甲销售点的水果200件,运往乙销售点的水果120件.
24、AE=FC+EF,证明见解析.
2023-2024学年山西省吕梁市兴县康宁中学九上数学期末质量跟踪监视模拟试题含答案: 这是一份2023-2024学年山西省吕梁市兴县康宁中学九上数学期末质量跟踪监视模拟试题含答案,共8页。试卷主要包含了答题时请按要求用笔,方程的根是,方程﹣1=的解是,定义等内容,欢迎下载使用。
2023-2024学年山西省吕梁市兴县康宁中学数学九上期末质量跟踪监视模拟试题含答案: 这是一份2023-2024学年山西省吕梁市兴县康宁中学数学九上期末质量跟踪监视模拟试题含答案,共7页。试卷主要包含了下列说法,如图所示的几何体,它的左视图是等内容,欢迎下载使用。
2023-2024学年山西省吕梁市兴县康宁中学八上数学期末质量检测试题含答案: 这是一份2023-2024学年山西省吕梁市兴县康宁中学八上数学期末质量检测试题含答案,共8页。试卷主要包含了的平方根是等内容,欢迎下载使用。












