


山西省2022-2023学年数学七年级第二学期期末经典试题含答案
展开山西省2022-2023学年数学七年级第二学期期末经典试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考试结束后,请将本试卷和答题卡一并交回.
2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.
4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.
5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗.
一、选择题(每小题3分,共30分)
1.调查50名学生的年龄,列频数分布表时,这些学生的年龄落在5个小组中,第一、二、三、五组数据个数分别是2,8,15,5,则第四组的频数是( )
A.20 B.30 C.0.4 D.0.6
2.下列四个图形分别是四届国际数学家大会的会标,其中属于中心对称图形的有( )
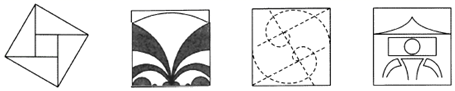
A.1个 B.2个 C.3个 D.4个
3.关于![]() 的一元二次方程
的一元二次方程![]() (
(![]() ,
,![]() 是常数,且
是常数,且![]() ),( )
),( )
A.若![]() ,则方程可能有两个相等的实数根 B.若
,则方程可能有两个相等的实数根 B.若![]() ,则方程可能没有实数根
,则方程可能没有实数根
C.若![]() ,则方程可能有两个相等的实数根 D.若
,则方程可能有两个相等的实数根 D.若![]() ,则方程没有实数根
,则方程没有实数根
4.某商品四天内每天每斤的进价与售价信息如图所示,则售出这种商品每斤利润最大的是( )
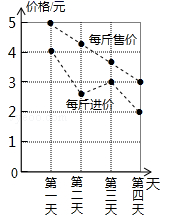
A.第一天 B.第二天 C.第三天 D.第四天
5.如图,有一块Rt△ABC的纸片,∠ABC=![]() ,AB=6,BC=8,将△ABC沿AD折叠,使点B落在AC上的E处,则BD的长为( )
,AB=6,BC=8,将△ABC沿AD折叠,使点B落在AC上的E处,则BD的长为( )
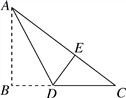
A.3 B.4 C.5 D.6
6.不等式组![]() 的解集是x>1,则m的取值范围是( )
的解集是x>1,则m的取值范围是( )
A.m≥1 B.m≤1 C.m≥0 D.m≤0
7.如图,在矩形ABCD中,AB=1,AD=![]() ,AF平分∠DAB,过C点作CE⊥BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED。正确的是( )
,AF平分∠DAB,过C点作CE⊥BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED。正确的是( )
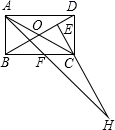
A.②③ B.②③④ C.③④ D.①②③④
8.以下列各组数为边长,能构成直角三角形的是( )
A.2,3,4 B.3,4,6 C.5,12,13 D.1,2,3
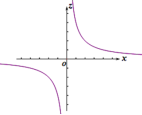
9.设函数![]() (
(![]() ≠0)的图象如图所示,若
≠0)的图象如图所示,若![]() ,则
,则![]() 关于
关于![]() 的函数图象可能为( )
的函数图象可能为( )
A.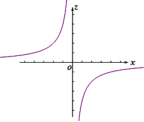 B.
B.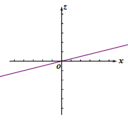 C.
C.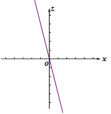 D.
D.
10.小明为画一个零件的轴截面,以该轴截面底边所在的直线为x轴,对称轴为y轴,建立如图所示的平面直角坐标系.若坐标轴的单位长度取1mm,则图中转折点![]() 的坐标表示正确的是
的坐标表示正确的是![]()
![]()
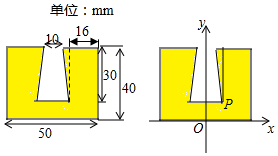
A.(5,30) B.(8,10) C.(9,10) D.(10,10)
二、填空题(本大题共有6小题,每小题3分,共18分)
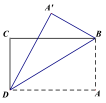
11.如图,把一张长方形的纸沿对角线BD折叠后,顶点A落在A′处,已知∠CDA′=28°,则∠CBD=______________.
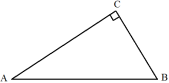
12.如图是一张三角形纸片,其中![]() ,从纸片上裁出一矩形,要求裁出的矩形的四个顶点都在三角形的边上,其面积为
,从纸片上裁出一矩形,要求裁出的矩形的四个顶点都在三角形的边上,其面积为![]() ,则该矩形周长的最小值=________
,则该矩形周长的最小值=________
13.关于x的方程![]() 有解,则k的范围是______.
有解,则k的范围是______.
14.要使四边形ABCD是平行四边形,已知∠A=∠C=120°,则还需补充一个条件是_____.
15. “同位角相等”的逆命题是__________________________.
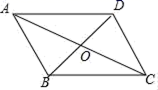
16.如图,▱ABCD的对角线交于点O,且AB=5,△OCD的周长为16,则▱ABCD的两条对角线的和是______
三、解下列各题(本大题共8小题,共72分)
17.(8分)观察下列一组方程:![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() 它们的根有一定的规律,都是两个连续的自然数,我们称这类一元二次方程为“连根一元二次方程”.
它们的根有一定的规律,都是两个连续的自然数,我们称这类一元二次方程为“连根一元二次方程”.
![]() 若
若![]() 也是“连根一元二次方程”,写出k的值,并解这个一元二次方程;
也是“连根一元二次方程”,写出k的值,并解这个一元二次方程;
![]() 请写出第n个方程和它的根.
请写出第n个方程和它的根.
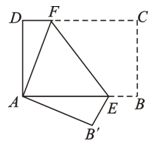
18.(8分)如图,将矩形纸片ABCD折叠,使点C与点A重合,折痕EF分别与AB、DC交于点E和点F, 点B的对应点为B′.
(1)证明:AE=CF;
(2)若AD=12,DC=18,求DF的长.
19.(8分)为了调查甲,乙两台包装机分装标准质量为![]() 奶粉的情况,质检员进行了抽样调查,过程如下.请补全表一、表二中的空,并回答提出的问题.
奶粉的情况,质检员进行了抽样调查,过程如下.请补全表一、表二中的空,并回答提出的问题.
收集数据:
从甲、乙包装机分装的奶粉中各自随机抽取10袋,测得实际质量(单位:![]() )如下:
)如下:
甲:394,400,408,406,410,409,400,400,393,395
乙:402,404,396,403,402,405,397,399,402,398
整理数据:
表一
频数种类 质量( | 甲 | 乙 |
| ____________ | 0 |
| 0 | 3 |
| 3 | 1 |
| 0 | ____________ |
| ____________ | 1 |
| 3 | 0 |
分析数据:
表二
种类 | 甲 | 乙 |
平均数 | 401.5 | 400.8 |
中位数 | ____________ | 402 |
众数 | 400 | ____________ |
方差 | 36.85 | 8.56 |
得出结论:
包装机分装情况比较好的是______(填甲或乙),说明你的理由.
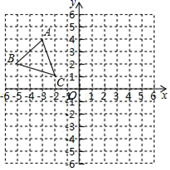
20.(8分)如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() .
.
(1)画出![]() 关于
关于![]() 轴的对称图形
轴的对称图形![]() ,并写出其顶点坐标;
,并写出其顶点坐标;
(2)画出将![]() 先向下平移4个单位,再向右平移3单位得到的
先向下平移4个单位,再向右平移3单位得到的![]() ,并写出其顶点坐标.
,并写出其顶点坐标.
21.(8分)先化简(![]() -m-2)÷
-m-2)÷![]() ,然后从-2<m≤2中选一个合适的整数作为m的值代入求值.
,然后从-2<m≤2中选一个合适的整数作为m的值代入求值.
22.(10分)计算:
(1)![]()
(2)(![]() ﹣
﹣![]() )(
)(![]() +
+![]() )+
)+![]() ×
×![]()
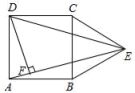
23.(10分)如图,在正方形ABCD的外侧,作等边三角形BCE,连接AE,DE.
(1)求证:AE=DE
(2)过点D作DF⊥AE,垂足为F,若AB=2cm,求DF的长.
24.(12分)(阅读材料)
解方程:![]() .
.
解:设![]() ,则原方程变为
,则原方程变为![]() .
.
解得,![]() ,
,![]() .
.
当![]() 时,
时,![]() ,解得
,解得![]() .
.
当![]() 时,
时,![]() ,解得
,解得![]() .
.
所以,原方程的解为![]() ,
,![]() ,
,![]() ,
,![]() .
.
(问题解决)
利用上述方法,解方程:![]() .
.
参考答案
一、选择题(每小题3分,共30分)
1、A
2、B
3、C
4、B
5、A
6、D
7、B
8、C
9、D
10、C
二、填空题(本大题共有6小题,每小题3分,共18分)
11、31°
12、![]()
13、k≤5
14、∠B=∠D=60°
15、如果两个角相等,那么这两个角是同位角.
16、1
三、解下列各题(本大题共8小题,共72分)
17、(1)x1=7,x2=8.(2)x1=n-1,x2=n.
18、(1)见解析;(2)5.
19、整理数据:3,1,5;分析数据:400,402;得出结论:乙,理由详见解析.
20、(1)图详见解析,![]() ;(2)图详见解析,
;(2)图详见解析,![]()
21、![]() ,
,![]() .
.
22、(1)![]() ;(2)3.
;(2)3.
23、(1)详见解析;(2)![]()
24、![]() ,
,![]() ,
,![]() ,
,![]()
山西省朔州市朔城区2022-2023学年七年级数学第二学期期末经典试题含答案: 这是一份山西省朔州市朔城区2022-2023学年七年级数学第二学期期末经典试题含答案,共7页。
山西省朔州市怀仁市2022-2023学年七年级数学第二学期期末经典模拟试题含答案: 这是一份山西省朔州市怀仁市2022-2023学年七年级数学第二学期期末经典模拟试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁,下列说法正确的是,下列命题中,为假命题的是等内容,欢迎下载使用。
山西省晋中学市榆次区2022-2023学年数学七年级第二学期期末经典试题含答案: 这是一份山西省晋中学市榆次区2022-2023学年数学七年级第二学期期末经典试题含答案,共7页。试卷主要包含了下列分式中,是最简分式的是等内容,欢迎下载使用。












