


安徽省重点中学2022-2023学年数学七年级第二学期期末学业质量监测模拟试题含答案
展开这是一份安徽省重点中学2022-2023学年数学七年级第二学期期末学业质量监测模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。
安徽省重点中学2022-2023学年数学七年级第二学期期末学业质量监测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生请注意:
1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如图,在△ABC中,AB=AC=10,BC=12,点D是BC上一点,DE∥AC,DF∥AB,则△BED与△DFC的周长的和为( )
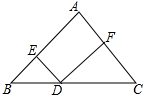
A.34 B.32 C.22 D.20
2.如图,在△ABC中,∠C=90°,∠B=15°,AC=3,AB的垂直平分线l交BC于点D,连接AD,则BC的长为( )
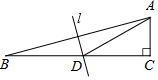
A.12 B.3![]() +3 C.6+3
+3 C.6+3![]() D.6
D.6![]()
3.若x-![]() ,则x-y的值为( )
,则x-y的值为( )
A.2 B.1 C.0 D.-1
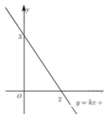
4.如图,已知一次函数![]() 的图象与
的图象与![]() 轴,
轴,![]() 轴分别交于点(2,0),点(0,3).有下列结论:①关于
轴分别交于点(2,0),点(0,3).有下列结论:①关于![]() 的方程
的方程![]() 的解为
的解为![]() ;②当
;②当![]() 时,
时,![]() ;③当
;③当![]() 时,
时,![]() . 其中正确的是( )
. 其中正确的是( )
A.①② B.①③ C.②③ D.①③②
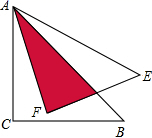
5.如图,将等腰直角三角形ABC绕点A逆时针旋转15度得到ΔAEF,若AC=![]() ,则阴影部分的面积为( )
,则阴影部分的面积为( )
A.1 B.![]() C.
C.![]() D.
D.![]()
6.若函数![]() ,则当函数值y=8时,自变量x的值是( )
,则当函数值y=8时,自变量x的值是( )
A.±![]() B.4 C.±
B.4 C.±![]() 或4 D.4或-
或4 D.4或-![]()
7.某班实行每周量化考核制,学期末对考核成绩进行统计,结果显示甲、乙两组的平均成绩相同,方差分别是S2甲=36,S2乙=30,则两组成绩的稳定性( )
A.甲组比乙组的成绩稳定 B.乙组比甲组的成绩稳定
C.甲、乙两组的成绩一样稳定 D.无法确定
8.甲安装队为 A小区安装 ![]() 台空调,乙安装队为 B小区安装
台空调,乙安装队为 B小区安装 ![]() 台空调,两队同时开工且恰好同时完工,甲队比乙队每天多安装
台空调,两队同时开工且恰好同时完工,甲队比乙队每天多安装 ![]() 台,设乙队每天安装
台,设乙队每天安装 ![]() 台,根据题意,下面所列方程中正确的是
台,根据题意,下面所列方程中正确的是 ![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
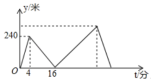
9.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟.在整个步行过程中,甲、乙两人的距离![]() (米)与甲出发的时间
(米)与甲出发的时间![]() (分)之间的关系如图所示,下列结论:①甲步行的速度为60米/分;②乙用16分钟追上甲;③乙走完全程用了30分钟;④乙到达终点时甲离终点还有360米.其中正确的结论有( )
(分)之间的关系如图所示,下列结论:①甲步行的速度为60米/分;②乙用16分钟追上甲;③乙走完全程用了30分钟;④乙到达终点时甲离终点还有360米.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
10.若反比例函数![]() 的图象在第二、四象限,则
的图象在第二、四象限,则![]() 的值是( )
的值是( )
A.-1或1 B.小于![]() 的任意实数 C.-1 D.不能确定
的任意实数 C.-1 D.不能确定
11.如果点 A(![]() ,
,![]() )和点 B(
)和点 B(![]() ,
,![]() )是直线 y=kx-b 上的两点,且当
)是直线 y=kx-b 上的两点,且当![]() <
<![]() 时,
时,![]() <
<![]() ,那么函数 y=
,那么函数 y= ![]() 的图象大致是()
的图象大致是()
A.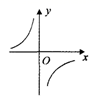 B.
B.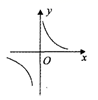
C.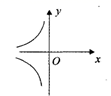 D.
D.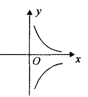
12.如图,有两个可以自由转动的转盘(每个转盘均被等分),同时转动这两个转盘,待转盘停止后,两个指针同时指在偶数上的概率是( )
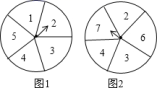
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.某种细菌的直径约为0.00 000 002米,用科学记数法表示该细菌的直径约为____米.
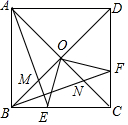
14.如图,在正方形ABCD中,AC、BD相交于点O,E、F分别为BC、CD上的两点,![]() ,AE、BF分别交BD、AC于M、N两点,连OE、
,AE、BF分别交BD、AC于M、N两点,连OE、![]() 下列结论:
下列结论:![]() ;
;![]() ;
;![]() ;
;![]() ,其中正确的序数是______.
,其中正确的序数是______.
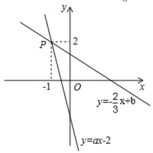
15.如图,已知一次函数y=−![]() x+b和y=ax−2的图象交于点P(−1,2),则根据图象可得不等式−
x+b和y=ax−2的图象交于点P(−1,2),则根据图象可得不等式−![]() x+b>ax−2的解集是______.
x+b>ax−2的解集是______.
16.若一元二次方程![]() (
(![]() 为常数)有两个相等的实数根,则
为常数)有两个相等的实数根,则![]() ______.
______.
17.若直角三角形的斜边长为6,则这个直角三角形斜边的中线长________.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)如图是一张长20cm、宽12cm的矩形纸板,将纸板四个角各剪去一个边长为![]() cm的正方形,然后将四周突出部分折起,可制成一个无盖纸盒.
cm的正方形,然后将四周突出部分折起,可制成一个无盖纸盒.
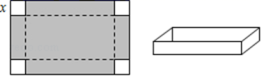
(1)这个无盖纸盒的长为 cm,宽为 cm;(用含x的式子表示)
(2)若要制成一个底面积是180m2的无盖长方体纸盒,求![]() 的值.
的值.
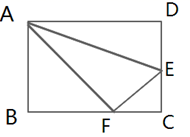
19.(5分)如图,折叠长方形一边AD,点D落在BC边的点F处,BC=10cm,AB=8cm.
求:(1)FC的长;(2)EF的长.
20.(8分)小诚响应“低碳环保,绿色出行”的号召,一直坚持跑步与步行相结合的上学方式![]() 已知小诚家距离学校2200米,他步行的平均速度为80米
已知小诚家距离学校2200米,他步行的平均速度为80米![]() 分,跑步的平均速度为200米
分,跑步的平均速度为200米![]() 分
分![]() 若他要在不超过20分钟的时间内从家到达学校,至少需要跑步多少分钟?
若他要在不超过20分钟的时间内从家到达学校,至少需要跑步多少分钟?
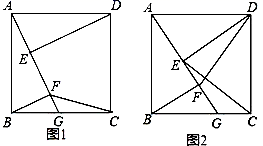
21.(10分)如图1,四边形ABCD是正方形,AB=4,点G在BC边上,BG=3,DE⊥AG于点E,BF⊥AG于点F.
(1)求BF和DE的长;
(2)如图2,连接DF、CE,探究并证明线段DF与CE的数量关系与位置关系.
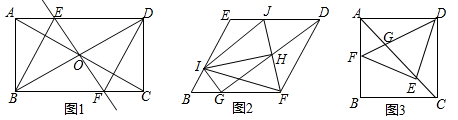
22.(10分)如图1,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,且交AC于点E,交BC于点F,连接BE、DF,且BE平分∠ABD.
(1)①求证:四边形BFDE是菱形;②求∠EBF的度数.
(2)把(1)中菱形BFDE进行分离研究,如图2,G,I分别在BF,BE边上,且BG=BI,连接GD,H为GD的中点,连接FH,并延长FH交ED于点J,连接IJ,IH,IF,IG.试探究线段IH与FH之间满足的数量关系,并说明理由;
(3)把(1)中矩形ABCD进行特殊化探究,如图3,矩形ABCD满足AB=AD时,点E是对角线AC上一点,连接DE,作EF⊥DE,垂足为点E,交AB于点F,连接DF,交AC于点G.请直接写出线段AG,GE,EC三者之间满足的数量关系.
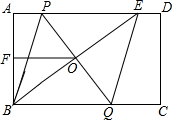
23.(12分)如图,在矩形ABCD中,E是AD边上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、QE
(1)求证:四边形BPEQ是菱形:
(2)若AB=6,F是AB中点,OF=4,求菱形BPEQ的面积.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、B
2、C
3、B
4、A
5、C
6、D
7、B
8、D
9、C
10、C
11、A
12、B
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、![]()
14、![]()
15、x>-1;
16、±2
17、1
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)(20﹣2x),(12﹣2x);(2)1
19、 (1)4cm;(2)5cm.
20、小诚至少需要跑步5分钟.
21、(1)![]() ;(2)DF=CE,DF⊥CE.理由见解析;
;(2)DF=CE,DF⊥CE.理由见解析;
22、(1)①证明见解析;②![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
23、(1)详见解析;(2)![]() .
.
相关试卷
这是一份郑州市重点中学2022-2023学年七年级数学第二学期期末学业质量监测模拟试题含答案,共6页。试卷主要包含了下列语句正确的是等内容,欢迎下载使用。
这是一份洛阳市重点中学2022-2023学年七年级数学第二学期期末学业质量监测模拟试题含答案,共6页。试卷主要包含了答题时请按要求用笔等内容,欢迎下载使用。
这是一份山东省重点中学2022-2023学年七年级数学第二学期期末学业质量监测模拟试题含答案,共8页。试卷主要包含了已知,则等内容,欢迎下载使用。












