

洛阳市重点中学2022-2023学年七年级数学第二学期期末学业质量监测模拟试题含答案
展开洛阳市重点中学2022-2023学年七年级数学第二学期期末学业质量监测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如图,点D是等边△ABC的边AC上一点,以BD为边作等边△BDE,若BC=10,BD=8,则△ADE的周长为( )
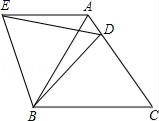
A.14 B.16 C.18 D.20
2.一辆慢车以50千米/小时的速度从甲地驶往乙地,一辆快车以75千米/小时的速度从乙地驶往甲地,甲、乙两地之间的距离为500千米,两车同时出发,则图中折线大致表示两车之间的距离y(千米)与慢车行驶时间t(小时)之间的函数图象是( )
A.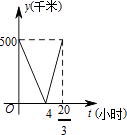 B.
B.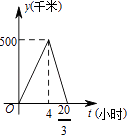 C.
C.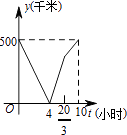 D.
D.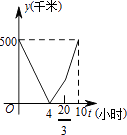
3.已知菱形的边长等于2cm,菱形的一条对角线也是长2cm,则另一条对角线长是( )
A.4cm B.2![]() cm C.
cm C.![]() cm D.3cm
cm D.3cm
4.ABCD是一块正方形场地,小华和小萌在AB上取一点E,测量得![]() ,
,![]() ,这块场地的对角线长是( )
,这块场地的对角线长是( )
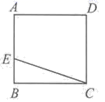
A.10 B.30 C.40 D.50
5.小颖从家出发,走了20分钟,到一个离家1000米的图书室,看了40分钟的书后,用15分钟返回到家,图(3)中表示小颖离家时间x与距离y之间的关系正确的是( )
A.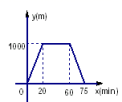 B.
B.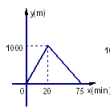 C.
C.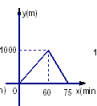 D.
D.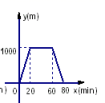
6.若A(2,y1),B(3,y2)是一次函数y=-3x+1的图象上的两个点,则y1与y2的大小关系是( )
A.y1<y2 B.y1=y2 C.y1>y2 D.不能确定
7.已知四边形ABCD中,AB∥CD,添加下列条件仍不能判断四边形ABCD是平行四边形的是( )
A.AB=CD B.AD=BC C.AD∥BC D.∠A+∠B=180°
8.下列各组数是三角形的三边长,能组成直角三角形的一组数是()
A.2,2,3 B.4,6,8 C.2,3,![]() D.
D.![]() ,
,![]() ,
,![]()
9.下列从左到右的变形,是因式分解的是( )
A.(x﹣y)(x+ y)= x2﹣y2 B.2x2+4xy = 2x(x+2y)
C.x2+2x+3 = x(x+2)+3 D.(m﹣2)2 = m2﹣4m+4
10.把一张正方形纸片按如图所示的方法对折两次后剪去两个角,那么打开以后的形状是( )
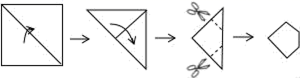
A.六边形 B.八边形 C.十二边形 D.十六边形
11.以下列各组线段为边,能构成直角三角形的是( )
A.1cm,2cm,3cm B.![]() cm,
cm,![]() cm,5cm C.6cm,8cm,10cm D.5cm,12cm,18cm
cm,5cm C.6cm,8cm,10cm D.5cm,12cm,18cm
12.我省2013年的快递业务量为1.2亿件,受益于电子商务发展和法治环境改善等多重因素,快递业务迅猛发展,2012年增速位居全国第一.若2015年的快递业务量达到2.5亿件,设2012年与2013年这两年的平均增长率为x,则下列方程正确的是( )
A.1.2(1+x)=2.5
B.1.2(1+2x)=2.5
C.1.2(1+x)2=2.5
D.1.2(1+x)+1.2(1+x)2=2.5
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.已知一次函数的图象与直线y=﹣x+1平行,且过点(8,2),那么此一次函数的解析式为 .
14.不等式组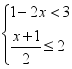 的所有整数解的积是___________.
的所有整数解的积是___________.
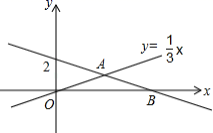
15.如图,直线y=![]() 与y=
与y=![]() x交于A(3,1)与x轴交于B(6,0),则不等式组0
x交于A(3,1)与x轴交于B(6,0),则不等式组0![]() 的解集为_____.
的解集为_____.
16.化简![]() 的结果为___________
的结果为___________
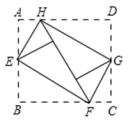
17.如图,将矩形ABCD的四个角向内翻折后,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12厘米,EF=16厘米,则边AD的长是________ cm.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
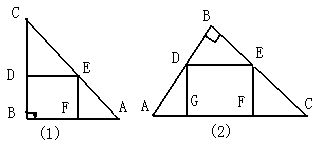
18.(5分)一块直角三角形木块的面积为1.5m2,直角边AB长1.5m,想要把它加工成一个面积尽可能大的正方形桌面,甲、乙两人的加工方法分别如图①、图②所示。你能用所学知识说明谁的加工方法更符合要求吗?
19.(5分)计算或化简:(1)![]() ;(2)
;(2)![]()
20.(8分)若抛物线上![]() ,它与
,它与![]() 轴交于
轴交于![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() ,
,![]() 是抛物线上
是抛物线上![]() 、
、![]() 之间的一点,
之间的一点,

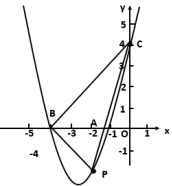
(1)当![]() 时,求抛物线的方程,并求出当
时,求抛物线的方程,并求出当![]() 面积最大时的
面积最大时的![]() 的横坐标.
的横坐标.
(2)当![]() 时,求抛物线的方程及
时,求抛物线的方程及![]() 的坐标,并求当
的坐标,并求当![]() 面积最大时
面积最大时![]() 的横坐标.
的横坐标.
(3)根据(1)、(2)推断![]() 的横坐标与
的横坐标与![]() 的横坐标有何关系?
的横坐标有何关系?
21.(10分)某项工程由甲乙两队分别单独完成,则甲队用时是乙队的1.5倍:若甲乙两队合作,则需12天完成,请问:
(1)甲,乙两队单独完成各需多少天;
(2)若施工方案是甲队先单独施工![]() 天,剩下工程甲乙两队合作完成,若甲队施工费用为每天1.5万元,乙队施工费为每天3.5万元求施工总费用
天,剩下工程甲乙两队合作完成,若甲队施工费用为每天1.5万元,乙队施工费为每天3.5万元求施工总费用![]() (万元)关于施工时间
(万元)关于施工时间![]() (天)的函数关系式
(天)的函数关系式
(3)在(2)的方案下,若施工期定为15~18天内完成(含15和18天),如何安排施工方案使费用最少,最少费用为多少万元?
22.(10分)如图,方格纸中每个小方格都是长为1个单位的正方形.若学校位置的坐标为A(1,2),解答以下问题:
(1)请在图中建立适当的直角坐标系,并写出图书馆B位置的坐标;
(2)若体育馆位置的坐标为C(-3,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.

23.(12分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、C
2、C
3、B
4、C
5、A
6、C
7、B
8、C
9、B
10、B
11、C
12、C
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、y=-x+1
14、1
15、3<x<1
16、![]()
17、20
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、甲的加工更符合要求.图①中正方形的边长是![]() ,图②中的正方形边长是
,图②中的正方形边长是![]() ,因为
,因为![]() >
>![]() ,所以甲的加工更符合要求.
,所以甲的加工更符合要求.
19、(1)![]() ;(2)
;(2)![]() .
.
20、(1)2;(2)-2;(3)![]() 的横坐标等于
的横坐标等于![]() 的横坐标的一半
的横坐标的一半
21、(1)甲、乙两队单独完成分别需30天,20天;(2)y=0.5x+60;(3)甲队先施工10天,再甲乙合作8天,费用最低为55万元
22、 (1) (-3,-2);(2)1.
23、(1)100+200x;(2)1.
郑州市重点中学2022-2023学年七年级数学第二学期期末学业质量监测模拟试题含答案: 这是一份郑州市重点中学2022-2023学年七年级数学第二学期期末学业质量监测模拟试题含答案,共6页。试卷主要包含了下列语句正确的是等内容,欢迎下载使用。
山东省重点中学2022-2023学年七年级数学第二学期期末学业质量监测模拟试题含答案: 这是一份山东省重点中学2022-2023学年七年级数学第二学期期末学业质量监测模拟试题含答案,共8页。试卷主要包含了已知,则等内容,欢迎下载使用。
安徽省重点中学2022-2023学年数学七年级第二学期期末学业质量监测模拟试题含答案: 这是一份安徽省重点中学2022-2023学年数学七年级第二学期期末学业质量监测模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。












