吉林省长春市绿园区2022-2023学年数学七年级第二学期期末考试模拟试题含答案

吉林省长春市绿园区2022-2023学年数学七年级第二学期期末考试模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

考生请注意：

1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。

2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。

3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。

一、选择题(每小题3分,共30分)

1．如图是甲、乙两个探测气球所在位置的海拔高度（单位：）关于上升时间（单位：）的函数图像.有下列结论：

①当时，两个探测气球位于同一高度

②当时，乙气球位置高；

③当时，甲气球位置高；

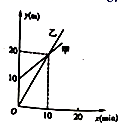
其中，正确结论的个数是（  ）

A．个 B．个 C．个 D．个

2．小苏和小林在如图①所示的跑道上进行米折返跑.在整个过程中，跑步者距起跑线的距离（单位：）与跑步时间（单位：）的对应关系如图②所示.下列叙述正确的是（    ）.

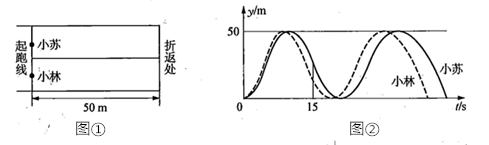
A．两人从起跑线同时出发，同时到达终点

B．小苏跑全程的平均速度大于小林跑全程的平均速度

C．小苏前跑过的路程大于小林前跑过的路程

D．小林在跑最后的过程中，与小苏相遇2次

3．下列计算正确的是（　　）

A．3﹣2＝1 B．（1﹣）（1+）＝﹣1

C．（2﹣）（3+）＝4 D．（+）2＝5

4．已知点P（a，m），Q（b，n）都在反比例函数y＝﹣的图象上，且a＜0＜b，则下列结论一定正确的是（　　）

A．m＜n B．m＞n C．m+n＜o D．m+n＞0

5．年一季度，华为某销公营收入比年同期增长，年第一季度营收入比年同期增长，年和年第一季度营收入的平均增长率为，则可列方程(   )

A． B．

C． D．

6．如图,在R△ABC中,∠ACB=90°,D为斜边AB的中点,动点P从点B出发,沿B→C→A运动,如图(1)所示,设,点P运动的路程为,若与之间的函数图象如图(2)所示,则的值为

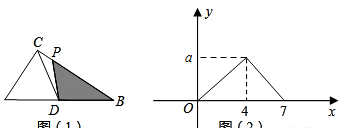
A．3 B．4 C．5 D．6

7．已知关于的一元二次方程的一个根是，则的值为（    ）

A． B． C． D．

8．若正比例函数的图像经过点，则这个图像必经过点(    )

A． B． C． D．

9．数学课上，小明同学在练习本的相互平行的横隔线上先画了直线a，度量出∠1＝112°，接着他准备在点A处画直线b．若要b∥a，则∠2的度数为(   )

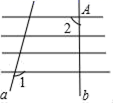
A．112° B．88° C．78° D．68°

10．如图，平行四边形 ABCD 中，AD∥BC，AB=BC=CD=AD=4，∠A=∠C=60°，连接 BD，将△BCD 绕点 B 旋转，当 BD（即 BD′）与 AD 交于一点 E，BC（即 BC′）同时与 CD 交于一点 F 时，下列结论正确的是（    ）

①AE=DF；②∠BEF=60°；③∠DEB=∠DFB；④△DEF 的周长的最小值是4+2

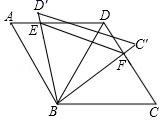
A．①② B．②③ C．①②④ D．①②③④

二、填空题(本大题共有6小题，每小题3分，共18分)

11．在Rt△ABC中，∠C＝90°，△ABC的周长为，其中斜边的长为2，则这个三角形的面积为_____________。

12．如图．将平面内Rt△ABC绕着直角顶点C逆时针旋转90°得到Rt△EFC．若AC=2，BC=1，则线段BE的长为__________．

13．若二次根式有意义，则x的取值范围是_____．

14．式子在实数范围内有意义，则 x 的取值范围是_______ ．

15．已知一组数据 a，b，c，d的方差是4，那么数据，，， 的方差是________．

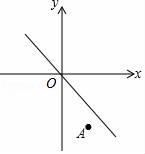
16．如图，将直线沿轴向下平移后的直线恰好经过点，且与轴交于点，在x轴上存在一点P使得的值最小，则点P的坐标为          ．

三、解下列各题(本大题共8小题，共72分)

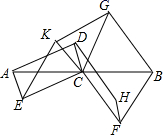
17．（8分）如图，设线段AB的中点为C，以AC和CB为对角线作平行四边形AECD、又作平行四边形CFHD、CGKE．

求证：H，C，K三点共线．

18．（8分）如图，在矩形ABCD中，E、F分别是边AB、CD的中点，连接AF，CE

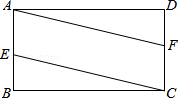
（1）求证：△BEC≌△DFA；

（2）求证：四边形AECF是平行四边形．

19．（8分）（本题满分6分）如图所示的方格地面上，标有编号1、2、3的3

个小方格地面是空地，另外6个小方格地面是草坪，除此以外小方格地

面完全相同．

 (1)一只自由飞行的小鸟，将随意地落在图中所示的方格地面上，求

小鸟落在草坪上的概率；

 (2)现准备从图中所示的3个小方格空地中任意选取2个种植草坪，

则编号为1、2的2个小方格空地种植草坪的概率是多少（用树状图或列表法求解）？

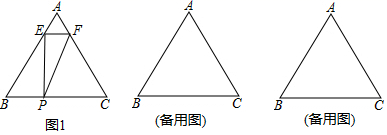
20．（8分）如图1，在等边△ABC中，AB=BC=AC=8cm，现有两个动点E，P分别从点A和点B同时出发，其中点E以1cm/秒的速度沿AB向终点B运动；点P以2cm/秒的速度沿射线BC运动．过点E作EF∥BC交AC于点F，连接EP，FP．设动点运动时间为t秒（0＜t≤8）．

（1）当点P在线段BC上运动时，t为何值，四边形PCFE是平行四边形？请说明理由；

（2）设△EBP的面积为y（cm2），求y与t之间的函数关系式；

（3）当点P在射线BC上运动时，是否存在某一时刻t，使点C在PF的中垂线上？若存在，请直接给出此时t的值（无需证明），若不存在，请说明理由．

21．（8分）先化简，再求代数式的值，其中.

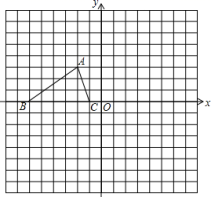
22．（10分）如图所示，已知△ABC的三个顶点的坐标分别为A(-2，3)，B(-6，0)，C(-1，0)．

(1)请直接写出点B关于点A对称的点的坐标；

(2)将△ABC绕坐标原点O逆时针旋转90°，画出图形，直接写出点B的对应点的坐标；

(3)请直接写出：以A、B、C为顶点的平行四边形的第四个顶点D的坐标．

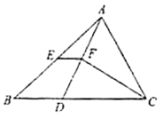
23．（10分）如图所示，在中，点在上，于，且平分，.

求证：.

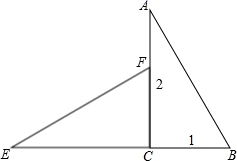
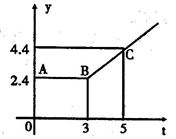
24．（12分）如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y（元）与通话时间t（分钟）之间的函数关系的图象．

（1）写出y与t之间的函数关系式；

（2）通话2分钟应付通话费多少元？通话7分钟呢？

参考答案

一、选择题(每小题3分,共30分)

1、D

2、D

3、B

4、B

5、D

6、A

7、C

8、B

9、D

10、C

二、填空题(本大题共有6小题，每小题3分，共18分)

11、0.5

12、1

13、x≥

14、x≥1

15、

16、（，0）

三、解下列各题(本大题共8小题，共72分)

17、证明见解析.

18、（1）证明见解析，（2）证明见解析

19、解: (1) 小鸟落在草坪上的概率为。

 (2)用树状图列出所有可能的结果：

开始

1 2 3

 2   3   1   3   1   2

所以编号为1、2的2个小方格空地种植草坪的概率是。

20、（1）t=；（2）y-t2+4t（0＜t≤8）；（3）t=时，点C在PF的中垂线上．

21、

22、（1）(2，6)；（2）作图见解析，点B'的坐标(0，-6)；（3）(-7，3)，(3，3)，(-5，-3)

23、详见解析

24、（1）当0<t≤3时，y=2.4；当t>3时，y=t-0.6；（2）2.4元；6.4元