北京一零一中学2022-2023学年七年级数学第二学期期末联考模拟试题含答案

北京一零一中学2022-2023学年七年级数学第二学期期末联考模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

考生须知：

1．全卷分选择题和非选择题两部分，全部在答题纸上作答。选择题必须用2B铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。

2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。

3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。

一、选择题(每小题3分,共30分)

1．如图，矩形ABCD中，对角线AC，BD相交于点O，下列结论不一定成立的是　　

A．

B．

C．

D．

2．位参加歌唱比赛的同学的成绩各不相同，按成绩取前位进入决赛。如果小尹知道了自己的成绩后，要判断自己能否进入决赛，他还要知道这位同学成绩的（）

A．平均数 B．众数 C．方差 D．中位数

3．下列说法中，不正确的有(     )

①一组数据的方差越大，这组数据的波动反而越小

②一组数据的中位数就是这组数据最中间的数

③在一组数据中，出现次数最多的数据称为这组数据的众数

A．①② B．①③ C．②③ D．③

4．某同学五天内每天完成家庭作业的时间（时）分别为2，3，2，1，2，则对这组数据的下列说法中错误的是（　　）

A．平均数是2 B．众数是2 C．中位数是2 D．方差是2

5．为迎接端午促销活动，某服装店从6月份开始对春装进行“折上折“(两次打折数相同)优惠活动，已知一件原价500元的春装，优惠后实际仅需320元，设该店春装原本打x折，则有

A． B．

C． D．

6．下列命题的逆命题，是假命题的是（   ）

A．两直线平行，内错角相等 B．全等三角形的对应边相等

C．对顶角相等 D．有一个角为度的三角形是直角三角形

7．如图，在△ABC中，∠B＝90°，以A为圆心，AE长为半径画弧，分别交AB、AC于F、E两点；分别以点E和点F为圆心，大于EF且相等的长为半径画弧，两弧相交于点G，作射线AG，交BC于点D，若BD＝，AC长是分式方程的解，则△ACD的面积是（　　）

A． B． C．4 D．3

8．函数中自变量x的取值范围是（ ）

A．≥－3 B．≥－3且 C． D．且

9．如图，在边长为4的正方形ABCD中，点E、F分别是边BC、CD上的动点．且BE＝CF，连接BF、DE，则BF+DE的最小值为（    ）

A． B． C． D．

10．如图，在平面直角坐标系xOy中，点A、C、F在坐标轴上，E是OA的中点，四边形AOCB是矩形，四边形BDEF是正方形，若点C的坐标为(3，0)， 则点D的坐标为（  ）

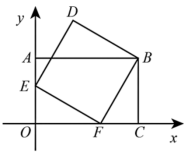
A．(1, 3) B．(1，) C．(1，) D．(，)

二、填空题(本大题共有6小题，每小题3分，共18分)

11．设甲组数：1，1，2，5的方差为S甲2，乙组数是：6，6，6，6的方差为S乙2，则S甲2与S乙2的大小关系是S甲2_____S乙2（选择“＞”、“＜”或“=”填空）．

12．如图，有两颗树，一颗高10米，另一颗高4米，两树相距8米.一只鸟从一颗树的树梢飞到另一颗树的树梢，问小鸟至少飞行_____米.

13．在平面直角坐标系中，点A（x，y）在第三象限，则点B（x，﹣y）在第_____象限．

14．不改变分式的值，使分子、分母的第一项系数都是正数，则＝_____．

15．在一张直角三角形纸片的两直角边上各取一点，分别沿斜边中点与这两点的连线剪去两个三角形，剩下的部分是如图所示的直角梯形，其中三边长分别为2、3、4，则原直角三角形纸片的斜边长是       .

16．某楼梯如图所示，欲在楼梯上铺设红色地毯，已知这种地毯每平方米售价为30元，楼梯宽为2m，则购买这种地毯至少需要_____元．

三、解下列各题(本大题共8小题，共72分)

17．（8分）如图，边长为 7 的正方形 OABC 放置在平面直角坐标系中，动点 P 从点 C 出发，以 每秒 1 个单位的速度向 O 运动，点 Q 从点 O 同时出发，以每秒 1 个单位的速度向点 A 运动，到达端点即停止运动，运动时间为 t 秒，连 PQ、BP、BQ．

（1）写出 B 点的坐标；

（2）填写下表：

①根据你所填数据，请描述线段 PQ 的长度的变化规律？并猜测 PQ 长度的最小值．

②根据你所填数据，请问四边形 OPBQ 的面积是否会发生变化？并证明你的论断；

（3）设点 M、N 分别是 BP、BQ 的中点，写出点 M，N 的坐标，是否存在经过 M， N 两点的反比例函数？如果存在，求出 t 的值；如果不存在，说明理由．

18．（8分）已知，如图：在平面直角坐标系中，O为坐标原点，四边形OABC是矩形，点A、C的坐标分别为、，点D是OA的中点，点P在BC边上运动，当是等腰三角形时，点Р的坐标为_______________．

19．（8分）如图，在Rt△ABC中，∠C＝90°，AB＝50，AC＝30，D，E，F分别是AC，AB，BC的中点．点P从点D出发沿折线DE－EF－FC－CD以每秒7个单位长的速度匀速运动；点Q从点B出发沿BA方向以每秒4个单位长的速度匀速运动，过点Q作射线QK⊥AB，交折线BC－CA于点G．点P，Q同时出发，当点P绕行一周回到点D时停止运动，点Q也随之停止．设点P，Q运动的时间是t秒（t>0）．

（1）D，F两点间的距离是          ；

（2）射线QK能否把四边形CDEF分成面积相等的两部分？若能，求出t的值．若不能，说明理由；

（3）当点P运动到折线EF－FC上，且点P又恰好落在射线QK上时，求t的值；

（4）连结PG，当PG∥AB时，请直接写出t的值．

20．（8分）某公司需招聘一名员工，对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核．甲、乙、丙各项得分如下表：

（1）根据三项得分的平均分，从高到低确定三名应聘者的排名顺序．

（2）该公司规定：笔试，面试、体能得分分别不得低于80分，80分，70分，并按60%，30%，10%的比例计入总分（不计其他因素条件），请你说明谁将被录用．

21．（8分）数学综合实验课上，同学们在测量学校旗杆的高度时发现：将旗杆顶端升旗用的绳子垂到地面还多2米；当把绳子的下端拉开8米后，下端刚好接触地面，如图，根据以上数据，同学们准确求出了旗杆的高度，你知道他们是如何计算出来的吗？

22．（10分）已知:在中, ,为的中点, , ,垂足分别为点,且.求证:是等边三角形.

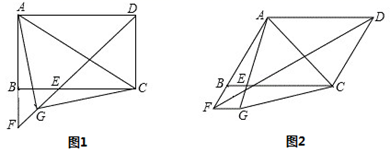
23．（10分）在ABCD中，∠ADC的平分线交直线BC于点E、交AB的延长线于点F，连接AC．

（1）如图1，若∠ADC=90°，G是EF的中点，连接AG、CG.

 ①求证：BE=BF；

 ②请判断△AGC的形状，并说明理由.

（2）如图2，若∠ADC=60°，将线段FB绕点F顺时针旋转60°至FG，连接AG、CG，判断△AGC的形状.（直接写出结论不必证明）

24．（12分）我国南宋时期数学家秦九昭及古希腊的几何学家海伦对于问题：“已知三角形的三边，如何求三角形的面积”进行了研究，并得到了海伦—秦九昭公式：如果一个三角形的三条边分别为，记，那么三角形的面积为，请用此公式求解：在中，，，，求的面积.

参考答案

一、选择题(每小题3分,共30分)

1、D

2、D

3、A

4、D

5、C

6、C

7、A

8、B

9、C

10、A

二、填空题(本大题共有6小题，每小题3分，共18分)

11、＞

12、1米

13、二

14、

15、2或10.

16、1

三、解下列各题(本大题共8小题，共72分)

17、（1）B（7，7）；（2）表格填写见解析；①,PQ长度的最小值是；

②四边形OPBQ的面积不会发生变化；（3）t=3.5存在经过M，N两点的反比例函数.

18、，，，；

19、（1）25；（2）能，t=；（3），；（4）和

20、（1）丙，乙，甲；（2）甲被录用．

21、旗杆的高度为12米．

22、证明见解析.

23、（1）①证明见解析；②△AGC是等腰直角三角形．证明见解析；（2）△AGC是等边三角形. 

24、