


云南省普洱市思茅区第四中学2022-2023学年数学七下期末考试试题含答案
展开云南省普洱市思茅区第四中学2022-2023学年数学七下期末考试试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如图,△ABC 称为第 1 个三角形,它的周长是 1,以它的三边中点为顶点组成第 2 个三角形,再以第 2 个三角形的三边中点为顶点组成第 3 个三角形,以此类推,则第 2019 个三角形的周长为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.货车行驶 25 千米与小车行驶 35 千米所用时间相同,已知小车每小时比货车多行驶 20千米,求两车的速度各为多少?设货车的速度为 x 千米/小时,依题意列方程正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.如果把![]() 分式中的
分式中的![]() 、
、![]() 都扩大到10倍,那么分式的值( )
都扩大到10倍,那么分式的值( )
A.扩大10倍 B.不变 C.扩大20倍 D.是原来的![]()
4.下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:

根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择 ( )
A.甲 B.乙 C.丙 D.丁
5.已知,顺次连接矩形各边的中点,得到一个菱形,如图1;再顺次连接菱形各边的中点,得到一个新的矩形,如图2;然后顺次连接新的矩形各边的中点得到一个新的菱形,如图3;……如此反复操作下去,则第2018个图形中直角三角形的个数有( )
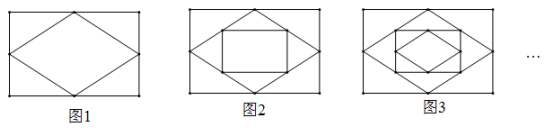
A.2018个 B.2017个 C.4028个 D.4036个
6.某交警在一个路口统计的某时段来往车辆的车速情况如表:
车速(km/h) | 48 | 49 | 50 | 51 | 52 |
车辆数(辆) | 5 | 4 | 8 | 2 | 1 |
则上述车速的中位数和众数分别是( )
A.50,8 B.49,50 C.50,50 D.49,8
7.如图,正方形ABCD中,点E在BD上,且![]() ,延长CE交AD于F,则
,延长CE交AD于F,则![]() 为( )
为( )
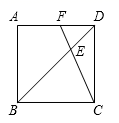
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.如图,E是平行四边形内任一点,若S平行四边形ABCD=8,则图中阴影部分的面积是( )
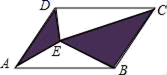
A.3 B.4 C.5 D.6
9.如图,已知平行四边形![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上一动点,作
上一动点,作![]() 于点
于点![]() ,作
,作![]() (
(![]() 在
在![]() 右边)且始终保持
右边)且始终保持![]() ,连接
,连接![]() 、
、![]() ,设
,设![]() ,则
,则![]() 满足( )
满足( )
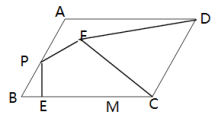
A.![]() B.
B.![]()
C.![]() D.
D.![]()
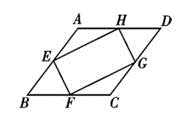
10.如图,在菱形ABCD中,点E,F,G,H分别是边AB,BC,CD和DA的中点,连接EF,FG,GH和HE,若EH=2EF=2,则菱形ABCD的边长为( )
A.![]()
![]() B.2
B.2 ![]()
![]() C.2
C.2 ![]() D.4
D.4
11.将两个全等的直角三角形纸片构成如图的四个图形,其中属于中心对称图形的是( )
A. B.
B. C.
C. D.
D.
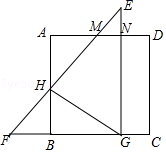
12.将正方形ABCD与等腰直角三角形EFG如图摆放,若点M、N刚好是AD的三等分点,下列结论正确的是( )
①△AMH≌△NME;②![]() ;③GH⊥EF;④S△EMN:S△EFG=1:16
;③GH⊥EF;④S△EMN:S△EFG=1:16
A.①②③④ B.①②③ C.①③④ D.①②④
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.因式分解:![]() .
.
14.如果关于x的分式方程![]() 有增根,则增根x的值为_____.
有增根,则增根x的值为_____.
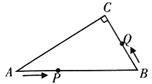
15.如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,若点P是边AB上的一个动点,以每秒3个单位的速度按照从
,若点P是边AB上的一个动点,以每秒3个单位的速度按照从![]() 运动,同时点Q从
运动,同时点Q从![]() 以每秒1个单位的速度运动,当一个动点到达终点时,另一个动点也随之停止运动。在运动过程中,设运动时间为t,若
以每秒1个单位的速度运动,当一个动点到达终点时,另一个动点也随之停止运动。在运动过程中,设运动时间为t,若![]() 为直角三角形,则t的值为________.
为直角三角形,则t的值为________.
16.一般地,在平面直角坐标系中,我们求点到直线间的距离,可用下面的公式求解:
点![]() 到直线
到直线![]() 的距离
的距离![]() 公式是:
公式是:![]()
如:求:点![]() 到直线
到直线![]() 的距离.
的距离.
解:由点到直线的距离公式,得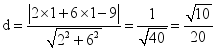
根据平行线的性质,我们利用点到直线的距离公式,也可以求两平行线间的距离.
则两条平行线![]() :
:![]() 和
和![]() :
:![]() 间的距离是______.
间的距离是______.
17.已知一元二次方程![]() ,则根的判别式△=____________.
,则根的判别式△=____________.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)某公司对应聘者A,B,进行面试,并按三个方面给应聘者打分,每方面满分20分,最后打分结果如下表,
| 专业知识 | 工作经验 | 仪表形象 |
A | 14 | 18 | 12 |
B | 18 | 16 | 11 |
根据实际需要,公司将专业知识、工作经验和仪表形象三项成绩得分按6:3:1的比例确定各人的成绩,此时谁将被录用?
19.(5分)解方程:![]() +
+![]() =1.
=1.
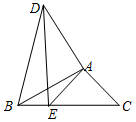
20.(8分)如图,将△ABC绕点A顺时针旋转得到△ADE(点B,C的对应点分别是D,E),当点E在BC边上时,连接BD,若∠ABC=30°,∠BDE=10°,求∠EAC.
21.(10分)如图,在□ABCD中,E、F分别是BC、AD上的点,且AE∥CF,AE与CF相等吗?说明理由.

22.(10分)如图,在矩形![]() 中,
中,![]() 、
、![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 的平行线
的平行线![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
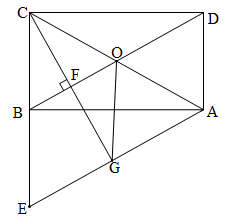
(1)求证:![]() .
.
(2)过点![]() 作
作![]() 于点
于点![]() ,并延长
,并延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .若
.若![]() ,
,![]() ,求四边形
,求四边形![]() 的周长.
的周长.
23.(12分)某校组织春游活动,提供了A、B、C、D四个景区供学生选择,并把选择最多的景区作为本次春游活动的目的地。经过抽样调查,并将采集的数据绘制成如下两幅不完整的统计图,请根据图①、②所提供的信息,解答下列问题:
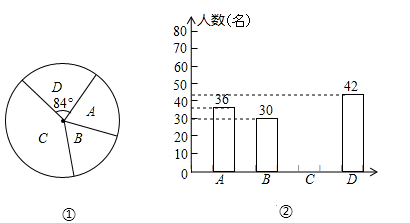
(1)本次抽样调查的学生有______名,其中选择景区A的学生的频率是______:
(2)请将图②补充完整:
(3)若该校共有1200名学生,根据抽样调查的结果估计全校共有多少名学生选择景区C?(要有解答过程)
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、B
2、C
3、A
4、A
5、D
6、C
7、B
8、B
9、D
10、A
11、C.
12、A
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、![]()
14、x=1
15、![]() 或
或![]() 或
或![]()
16、![]()
17、0
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、B应被录用
19、![]()
20、∠EAC=100°.
21、AE=CF.理由见解析.
22、(1)证明见解析;(2)![]() .
.
23、(1)180,![]() ;(2)见解析;(3)全校选择景区C的人数是480人.
;(2)见解析;(3)全校选择景区C的人数是480人.
云南省普洱市思茅区第四中学2023-2024学年数学九年级第一学期期末检测试题含答案: 这是一份云南省普洱市思茅区第四中学2023-2024学年数学九年级第一学期期末检测试题含答案,共7页。试卷主要包含了一元二次方程的根是,如图,是的直径,、是弧等内容,欢迎下载使用。
云南省普洱市思茅区第四中学2023-2024学年八上数学期末综合测试模拟试题含答案: 这是一份云南省普洱市思茅区第四中学2023-2024学年八上数学期末综合测试模拟试题含答案,共7页。试卷主要包含了已知,如图点A,下列各式中是完全平方式的是等内容,欢迎下载使用。
2022-2023学年云南省普洱市数学七下期末质量跟踪监视模拟试题含答案: 这是一份2022-2023学年云南省普洱市数学七下期末质量跟踪监视模拟试题含答案,共7页。












