


2022-2023学年普洱市重点中学数学七下期末质量检测试题含答案
展开
这是一份2022-2023学年普洱市重点中学数学七下期末质量检测试题含答案,共7页。试卷主要包含了下列运算,正确的是等内容,欢迎下载使用。
2022-2023学年普洱市重点中学数学七下期末质量检测试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 请考生注意:1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。 一、选择题(每小题3分,共30分)1.已知正比例函数y=kx(k≠0)的函数值y随x的增大而增大,则一次函数y=-kx+k的图像大致是( )A.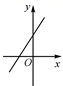 B.
B.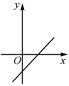 C.
C.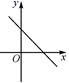 D.
D.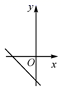 2.一次函数y=﹣x+6的图象上有两点A(﹣1,y1)、B(2,y2),则y1与y2的大小关系是( )A.y1>y2 B.y1=y2 C.y1<y2 D.y1≥y23.如图,在平行四边形
2.一次函数y=﹣x+6的图象上有两点A(﹣1,y1)、B(2,y2),则y1与y2的大小关系是( )A.y1>y2 B.y1=y2 C.y1<y2 D.y1≥y23.如图,在平行四边形![]() 中,对角线
中,对角线![]() 交于点
交于点![]() ,并且
,并且![]() ,点
,点![]() 是
是![]() 边上一动点,延长
边上一动点,延长![]() 交于
交于![]() 点
点![]() ,当点
,当点![]() 从点
从点![]() 向点
向点![]() 移动过程中(点
移动过程中(点![]() 与点
与点![]() ,
,![]() 不重合),则四边形
不重合),则四边形![]() 的变化是( )
的变化是( )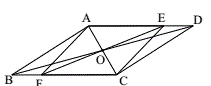 A.平行四边形→菱形→平行四边形→矩形→平行四边形B.平行四边形→矩形→平行四边形→菱形→平行四边形C.平行四边形→矩形→平行四边形→正方形→平行四边形D.平行四边形→矩形→菱形→正方形→平行四边形4.如图,将长方形纸片ABCD折叠,使点B与点D重合,折痕为EF,已知AB=6cm,BC=18cm,则Rt△CDF的面积是( )
A.平行四边形→菱形→平行四边形→矩形→平行四边形B.平行四边形→矩形→平行四边形→菱形→平行四边形C.平行四边形→矩形→平行四边形→正方形→平行四边形D.平行四边形→矩形→菱形→正方形→平行四边形4.如图,将长方形纸片ABCD折叠,使点B与点D重合,折痕为EF,已知AB=6cm,BC=18cm,则Rt△CDF的面积是( )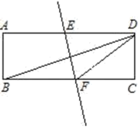 A.27cm2 B.24cm2 C.22cm2 D.20cm25.若代数式
A.27cm2 B.24cm2 C.22cm2 D.20cm25.若代数式![]() 在实数范围内有意义,则x的取值范围是( )A.x≥﹣2 B.x>﹣2 C.x≥2 D.x≤26.下列运算,正确的是( )A.
在实数范围内有意义,则x的取值范围是( )A.x≥﹣2 B.x>﹣2 C.x≥2 D.x≤26.下列运算,正确的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 7.如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,若AB=8,则CD的长是( )
7.如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,若AB=8,则CD的长是( )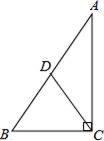 A.6 B.5 C.4 D.38.下面四个手机应用图标中是轴对称图形的是( )A.
A.6 B.5 C.4 D.38.下面四个手机应用图标中是轴对称图形的是( )A. B.
B. C.
C. D.
D. 9.如图,正方形网格中的每个小正方形的边长为1,将
9.如图,正方形网格中的每个小正方形的边长为1,将![]() 绕旋转中心旋转某个角度后得到
绕旋转中心旋转某个角度后得到![]() ,其中点A,B,C的对应点是点
,其中点A,B,C的对应点是点![]() ,
,![]() ,
,![]() ,那么旋转中心是( )
,那么旋转中心是( )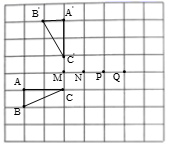 A.点Q B.点P C.点N D.点M10.一个圆锥形的圣诞帽高为 10cm,母线长为 15cm,则圣诞帽的表面积为( )A.75
A.点Q B.点P C.点N D.点M10.一个圆锥形的圣诞帽高为 10cm,母线长为 15cm,则圣诞帽的表面积为( )A.75![]() cm2 B.150
cm2 B.150![]() cm2 C.150
cm2 C.150![]() cm2 D.75
cm2 D.75![]() cm2二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,
cm2二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,![]() ,两条直线与这三条平行线分别交于点
,两条直线与这三条平行线分别交于点![]() 、
、![]() 、
、![]() 和
和![]() 、
、![]() 、
、![]() .已知
.已知![]() ,
,![]() ,
,![]() ,
,![]() 的长为_______.
的长为_______.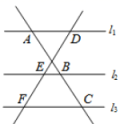 12.如图,在四边形ABCD中,点E、F分别是边AB、AD的中点,BC=15,CD=9,EF=6,∠AFE=50°,则∠ADC的度数为_____.
12.如图,在四边形ABCD中,点E、F分别是边AB、AD的中点,BC=15,CD=9,EF=6,∠AFE=50°,则∠ADC的度数为_____.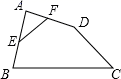 13.已知正多边形的一个外角等于40°,那么这个正多边形的边数为__________.14.如图,梯形ABCD中,AB∥CD,点E、F、G分别是BD、AC、DC的中点.已知两底差是6,两腰和是12,则△EFG的周长是 .
13.已知正多边形的一个外角等于40°,那么这个正多边形的边数为__________.14.如图,梯形ABCD中,AB∥CD,点E、F、G分别是BD、AC、DC的中点.已知两底差是6,两腰和是12,则△EFG的周长是 . 15.已知
15.已知![]() ,则
,则![]() 的值是_______.16.矩形的一边长是3.6㎝, 两条对角线的夹角为60º,则矩形对角线长是___________.三、解下列各题(本大题共8小题,共72分)17.(8分)先化简,再求值:
的值是_______.16.矩形的一边长是3.6㎝, 两条对角线的夹角为60º,则矩形对角线长是___________.三、解下列各题(本大题共8小题,共72分)17.(8分)先化简,再求值:![]() ÷(x﹣
÷(x﹣![]() ),其中x=
),其中x=![]() +1. 18.(8分)中国新版高铁“复兴号”率先在北京南站和上海虹桥站双向首发“复兴号”高铁从某车站出发,在行驶过程中速度
+1. 18.(8分)中国新版高铁“复兴号”率先在北京南站和上海虹桥站双向首发“复兴号”高铁从某车站出发,在行驶过程中速度![]() (千米/分钟)与时间
(千米/分钟)与时间![]() (分钟)的函数关系如图所示.
(分钟)的函数关系如图所示.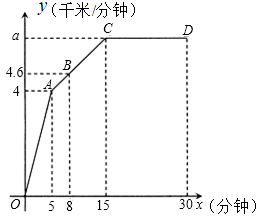 (1)当
(1)当![]() 时,求
时,求![]() 关于
关于![]() 工的函数表达式,(2)求点
工的函数表达式,(2)求点![]() 的坐标. (3)求高铁在
的坐标. (3)求高铁在![]() 时间段行驶的路程. 19.(8分)如图,正方形网格的每个小方格都是边长为1的正方形,△ABC的顶点都在格点上.(1)分别求出AB,BC,AC的长;(2)试判断△ABC是什么三角形,并说明理由.
时间段行驶的路程. 19.(8分)如图,正方形网格的每个小方格都是边长为1的正方形,△ABC的顶点都在格点上.(1)分别求出AB,BC,AC的长;(2)试判断△ABC是什么三角形,并说明理由.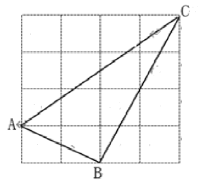 20.(8分)如图,一次函数
20.(8分)如图,一次函数![]() 的图象与
的图象与![]() ,
,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,点
两点,点![]() 与点
与点![]() 关于
关于![]() 轴对称.动点
轴对称.动点![]() ,
,![]() 分别在线段
分别在线段![]() ,
,![]() 上(点
上(点![]() 与点
与点![]() ,
,![]() 不重合),且满足
不重合),且满足![]() .(1)求点
.(1)求点![]() ,
,![]() 的坐标及线段
的坐标及线段![]() 的长度;(2)当点
的长度;(2)当点![]() 在什么位置时,
在什么位置时,![]() ,说明理由;(3)当
,说明理由;(3)当![]() 为等腰三角形时,求点
为等腰三角形时,求点![]() 的坐标.
的坐标.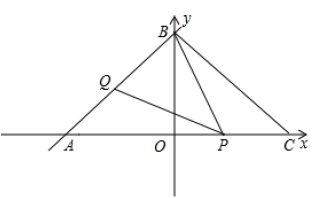 21.(8分)如图,已知△ABC的面积为3,且AB=AC,现将△ABC沿CA方向平移CA长度得到△EFA.(1)求四边形CEFB的面积;(2)试判断AF与BE的位置关系,并说明理由;(3)若∠BEC=15°,求AC的长.
21.(8分)如图,已知△ABC的面积为3,且AB=AC,现将△ABC沿CA方向平移CA长度得到△EFA.(1)求四边形CEFB的面积;(2)试判断AF与BE的位置关系,并说明理由;(3)若∠BEC=15°,求AC的长.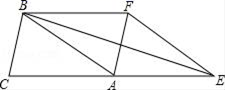 22.(10分)如图,△ABC是等边三角形,BD是中线,P是直线BC上一点.(1) 若CP=CD,求证:△DBP是等腰三角形;(2) 在图①中建立以△ABC的边BC的中点为原点,BC所在直线为x轴,BC边上的高所在直线为y轴的平面直角坐标系,如图②,已知等边△ABC的边长为2,AO=
22.(10分)如图,△ABC是等边三角形,BD是中线,P是直线BC上一点.(1) 若CP=CD,求证:△DBP是等腰三角形;(2) 在图①中建立以△ABC的边BC的中点为原点,BC所在直线为x轴,BC边上的高所在直线为y轴的平面直角坐标系,如图②,已知等边△ABC的边长为2,AO=![]() ,在x轴上是否存在除点P以外的点Q,使△BDQ是等腰三角形?如果存在,请求出Q点的坐标;如果不存在,请说明由.
,在x轴上是否存在除点P以外的点Q,使△BDQ是等腰三角形?如果存在,请求出Q点的坐标;如果不存在,请说明由.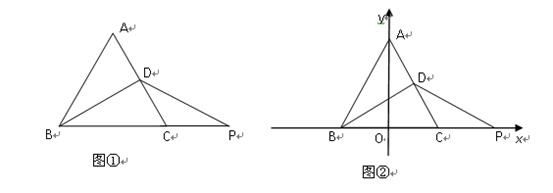 23.(10分)先化简,再求值,
23.(10分)先化简,再求值,![]() 从-1、1、2中选择一个你喜欢的且使原式有意义的
从-1、1、2中选择一个你喜欢的且使原式有意义的![]() 的值代入求值. 24.(12分)在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上),并新修一条路CH,测得CB=3千米,CH=2.4千米,HB=1.8千米.(1)问CH是否为从村庄C到河边的最近路?(即问:CH与AB是否垂直?)请通过计算加以说明;(2)求原来的路线AC的长.
的值代入求值. 24.(12分)在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上),并新修一条路CH,测得CB=3千米,CH=2.4千米,HB=1.8千米.(1)问CH是否为从村庄C到河边的最近路?(即问:CH与AB是否垂直?)请通过计算加以说明;(2)求原来的路线AC的长.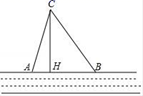 参考答案 一、选择题(每小题3分,共30分)1、D2、A3、A4、B5、C6、D7、C8、D9、C10、A 二、填空题(本大题共有6小题,每小题3分,共18分)11、
参考答案 一、选择题(每小题3分,共30分)1、D2、A3、A4、B5、C6、D7、C8、D9、C10、A 二、填空题(本大题共有6小题,每小题3分,共18分)11、![]() 12、140° 13、114、1.15、
12、140° 13、114、1.15、![]() 16、7.2cm或
16、7.2cm或![]() cm 三、解下列各题(本大题共8小题,共72分)17、
cm 三、解下列各题(本大题共8小题,共72分)17、![]() .18、(1)
.18、(1)![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() ;(3)高铁在
;(3)高铁在![]() 时段共行驶了
时段共行驶了![]() 千米.19、(1)
千米.19、(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() 是直角三角形,理由见解析20、(1)10;(2)当点
是直角三角形,理由见解析20、(1)10;(2)当点![]() 的坐标是
的坐标是![]() 时,
时,![]() ;(3)点
;(3)点![]() 的坐标是
的坐标是![]() 或
或![]() .21、(1)9;(2)BE⊥AF,理由详见解析;(3)
.21、(1)9;(2)BE⊥AF,理由详见解析;(3)![]() ;22、(1)见解析(2)P1(-
;22、(1)见解析(2)P1(-![]() -1,0),P2(0,0)P3(
-1,0),P2(0,0)P3(![]() +1,0)23、424、(1)CH是从村庄C到河边的最近路,理由见解析;(2)原来的路线AC的长为2.5千米.
+1,0)23、424、(1)CH是从村庄C到河边的最近路,理由见解析;(2)原来的路线AC的长为2.5千米.
相关试卷
这是一份2023-2024学年普洱市重点中学数学八上期末经典试题含答案,共8页。试卷主要包含了下列各数中,无理数的是,若3n+3n+3n=,则n=等内容,欢迎下载使用。
这是一份2022-2023学年连云港市重点中学数学七下期末质量检测试题含答案,共7页。
这是一份2022-2023学年绥化市重点中学数学七下期末复习检测模拟试题含答案,共7页。








