上海市浦东新区第一教育署2022-2023学年七下数学期末监测模拟试题含答案

上海市浦东新区第一教育署2022-2023学年七下数学期末监测模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项：

1． 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。

2．选择题必须使用2B铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。

3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。

4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．关于圆的性质有以下四个判断：①垂直于弦的直径平分弦，②平分弦的直径垂直于弦，③在同圆或等圆中，相等的弦所对的圆周角相等，④在同圆或等圆中，相等的圆周角所对的弦相等，则四个判断中正确的是（　　）

A．①③ B．②③ C．①④ D．②④

2．在一个不透明的盒子里装有2个红球和1个黄球，每个球除颜色外都相同，从中任意摸出2个球。下列事件中，不可能事件是（    ）

A．摸出的2个球都是红球

B．摸出的2个球都是黄球

C．摸出的2个球中有一个是红球

D．摸出的2个球中有一个是黄球

3．如图，在平行四边形ABCD中，O是对角线AC，BD的交点，下列结论错误的是（　　）

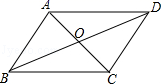
A．AB∥CD B．AC=BD C．AB=CD D．OA=OC

4．要使二次根式有意义，则x的取值范围是（      ）

A．x<3 B．x≤3 C．x>3 D．x≥3

5．甲、乙两车从A城出发匀速行驶至B城．在整个行驶过程中，甲、乙两车离开A城的距离y（千米）与甲车行驶的时间t（小时）之间的函数关系如图所示．则下列结论：①A，B两城相距300千米；②乙车比甲车晚出发1小时，却早到1.5小时；③乙车出发后2.5小时追上甲车；④当甲、乙两车相距40千米时，t＝或t＝，其中正确的结论有（　　）

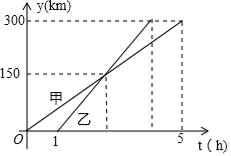
A．1个 B．2个 C．3个 D．4个

6．在Rt△ABC中，BC是斜边，∠B=40°，则∠C=（    ）

A．90° B．60° C．50° D．40°

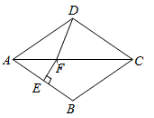
7．如图，在菱形中，，的垂直平分线交对角线于点,为垂足，连结，则等于（    ）

A． B． C． D．

8．下列各组长度的线段（单位：）中，成比例线段的是（    ）

A．1，2，3，4 B．1，2，3，6 C．2，3，4，5 D．1，3，5，10

9．某商店销售一批服装，每件售价150元，可获利25%，求这种服装的成本价．设这种服装的成本价为x元，则得到方程（　　）

A．＝25% B．150﹣x＝25% C．x＝150×25% D．25%x＝150

10．药品研究所开发一种抗菌新药，经过多年的动物实验之后首次用于临床人体试验，测得成人服药后血液中药物浓度（微克/毫升）与服药后的时间（时）之间的函数关系如图所示，则当，的取值范围是（    ）

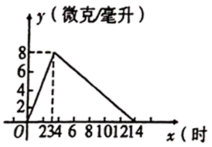
A． B． C． D．

11．将一次函数y=4x的图象向上平移3个单位长度，得到图象对应的函数解析式为（  ）

A．y=4x-3 B．y=2x-6 C．y=4x+3 D．y=-x-3

12．把一元二次方程配方后，下列变形正确的是（    ）

A． B． C． D．

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13．直线 y＝2x＋3 与 x 轴相交于点 A，则点 A 的坐标为_____．

14．若□ABCD中，∠A=50°，则∠C=_______°．

15．化简：＝_____．

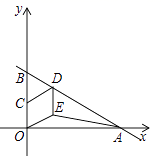
16．如图，直线与x轴、y轴分别交于A，B两点，C是OB的中点，D是AB上一点，四边形OEDC是菱形，则△OAE的面积为________．

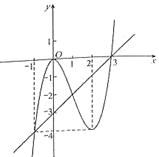
17．利用计算机中“几何画板”软件画出的函数和的图象如图所示．根据图象可知方程的解的个数为3个，若m，n分别为方程和的解，则m，n的大小关系是________.

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18．（5分）佳佳某天上午9时骑自行车离开家，17时回家，他有意描绘了离家的距离与时同的变化情况，如图所示.

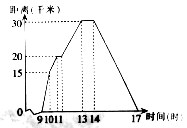
（1）图象表示了哪两个变量的关系？

（2）10时和11时，他分别离家多远？

（3）他最初到达离家最远的地方是什么时间？离家多远？

（4）11时到13时他行驶了多少千米？

19．（5分）计算：（1）；（2）+（3﹣2）（3+2）

20．（8分）已知，如图，在ABCD中，延长DA到点E，延长BC到点F，使得AE＝CF，连接EF，分别交AB，CD于点M，N，连接DM，BN.

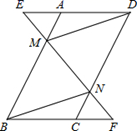
（1）求证：△AEM≌△CFN；

（2）求证：四边形BMDN是平行四边形.

21．（10分）已知，，求．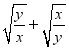

22．（10分）请阅读下列材料：

问题：现有5个边长为1的正方形，排列形式如图①，请把它们分割后拼接成一个新的正方形，要求：画出分割线并在正方形网格图（图中每个小正方形的边长均为1）中用实线画出拼接成的新正方形．小东同学的做法是：设新正方形的边长为x（x＞0），依题意，割补前后图形的面积相等，有x2＝5，解得，由此可知新正方形的边长等于两个小正方形组成的矩形对角线的长，于是，画出如图②所示的分割线，拼出如图③所示的新正方形．

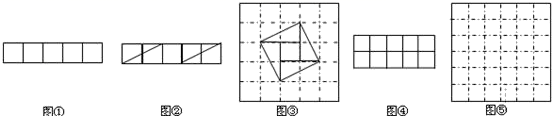
请你参考小东同学的做法，解决如下问题：

现有10个边长为1的正方形，排列形式如图④，请把它们分割后拼接成一个新的正方形，要求：在图④中画出分割线，并在图⑤的正方形网格图（图中每个小正方形的边长均为1）中用实线画出拼接成的新正方形．（说明：直接画出图形，不要求写分析过程．）

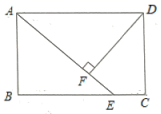
23．（12分）在矩形中，点在上，，，垂足为．

（1）求证：；

（2）若，且，求．

参考答案

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1、C

2、B

3、B

4、B

5、A

6、C

7、D

8、B

9、A

10、C

11、C

12、A

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13、（−，0）

14、50

15、1

16、

17、

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18、（1）图象表示离家距离与时间之间的关系；（2）10时和11时，他分别离家15千米、20千米；（3）他最初到达离家最远的地方是13时，离家30千米；（4）11时到13时他行驶了10千米．

19、（1）﹣；（2）1.

20、证明见解析

21、

22、见解析.

23、（1）见解析；（2）AD＝．