

2022-2023学年上海市浦东新区第四教育署数学七下期末检测模拟试题含答案
展开
这是一份2022-2023学年上海市浦东新区第四教育署数学七下期末检测模拟试题含答案,共7页。
2022-2023学年上海市浦东新区第四教育署数学七下期末检测模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。 一、选择题(每小题3分,共30分)1.定义:如果一元二次方程ax2+bx+c=0(a≠0)满足a+b+c=0,那么我们称这个方程为“和谐”方程;如果一元二次方程ax2+bx+c=0(a≠0)满足a﹣b+c=0那么我们称这个方程为“美好”方程,如果一个一元二次方程既是“和谐”方程又是“美好”方程,则下列结论正确的是( )A.方有两个相等的实数根 B.方程有一根等于0C.方程两根之和等于0 D.方程两根之积等于02.正方形具有而菱形不一定具有的性质是 ( )A.对角线相等 B.对角线互相垂直平分C.四条边相等 D.对角线平分一组对角3.甲从商贩A处购买了若干斤西瓜,又从商贩B处购买了若干斤西瓜.A、B两处所购买的西瓜重量之比为3:2,然后将买回的西瓜以从A、B两处购买单价的平均数为单价全部卖给了乙,结果发现他赔钱了,这是因为( )A.商贩A的单价大于商贩B的单价B.商贩A的单价等于商贩B的单价C.商版A的单价小于商贩B的单价D.赔钱与商贩A、商贩B的单价无关4.在![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中,分式的个数是( )A.2 B.3 C.4 D.55.将函数y=﹣3x的图象沿y轴向上平移2个单位长度后,所得图象对应的函数关系式为( )A.
中,分式的个数是( )A.2 B.3 C.4 D.55.将函数y=﹣3x的图象沿y轴向上平移2个单位长度后,所得图象对应的函数关系式为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 6.下列各组数为勾股数的是( )A.1,1,
6.下列各组数为勾股数的是( )A.1,1,![]() B.4,5,6 C.8,9,10 D.5,12,137.已知a>b,且a≠0,b≠0,a+b≠0,则函数y=ax+b与
B.4,5,6 C.8,9,10 D.5,12,137.已知a>b,且a≠0,b≠0,a+b≠0,则函数y=ax+b与![]() 在同一坐标系中的图象不可能是( )A.
在同一坐标系中的图象不可能是( )A.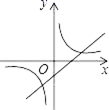 B.
B.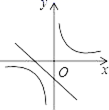 C.
C.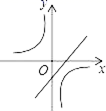 D.
D.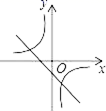 8.某校九年级(1)班全体学生体能测试成绩统计如下表(总分30分):成绩(分)24252627282930人数(人)2566876根据上表中的信息判断,下列结论中错误的是( )A.该班一共有40名同学 B.成绩的众数是28分C.成绩的中位数是27分 D.成绩的平均数是27.45分9.下列几红数中,是勾股数的有( ).①5、12、13;②13、14、15;③3k、4k、5k(k为正整数);④
8.某校九年级(1)班全体学生体能测试成绩统计如下表(总分30分):成绩(分)24252627282930人数(人)2566876根据上表中的信息判断,下列结论中错误的是( )A.该班一共有40名同学 B.成绩的众数是28分C.成绩的中位数是27分 D.成绩的平均数是27.45分9.下列几红数中,是勾股数的有( ).①5、12、13;②13、14、15;③3k、4k、5k(k为正整数);④![]() 、2、
、2、![]() .A.1组 B.2组 C.3组 D.4组10.根据如图所示的程序计算函数y的值,若输入的x值是﹣3和2时,输出的y值相等,则b等于( )
.A.1组 B.2组 C.3组 D.4组10.根据如图所示的程序计算函数y的值,若输入的x值是﹣3和2时,输出的y值相等,则b等于( )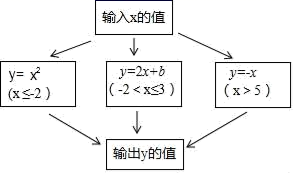 A.5 B.﹣5 C.7 D.3和4二、填空题(本大题共有6小题,每小题3分,共18分)11.正比例函数y=kx的图象与直线y=﹣x+1交于点P(a,2),则k的值是_____.12.表①给出了直线l1上部分(x,y)坐标值,表②给出了直线l2上部分点(x,y)坐标值,那么直线l1和直线l2的交点坐标为_______.
A.5 B.﹣5 C.7 D.3和4二、填空题(本大题共有6小题,每小题3分,共18分)11.正比例函数y=kx的图象与直线y=﹣x+1交于点P(a,2),则k的值是_____.12.表①给出了直线l1上部分(x,y)坐标值,表②给出了直线l2上部分点(x,y)坐标值,那么直线l1和直线l2的交点坐标为_______.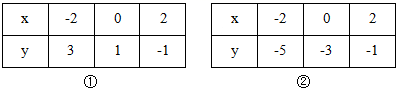 13. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若ab=8,大正方形的面积为25,则小正方形的边长为_____.
13. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若ab=8,大正方形的面积为25,则小正方形的边长为_____.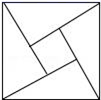 14.已知空气的密度是0.001239
14.已知空气的密度是0.001239![]() ,用科学记数法表示为________
,用科学记数法表示为________![]() 15.如图,在▱ABCD中,∠A=72°,将□ABCD绕顶点B顺时针旋转到▱A1BC1D1,当C1D1首次经过顶点C时,旋转角∠ABA1=_____°.
15.如图,在▱ABCD中,∠A=72°,将□ABCD绕顶点B顺时针旋转到▱A1BC1D1,当C1D1首次经过顶点C时,旋转角∠ABA1=_____°.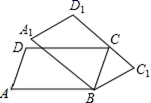 16.在一个不透明的袋子里装有3个白色乒乓球和若干个黄色乒乓球,若从这个袋子里随机摸出一个乒乓球,恰好是黄球的概率为0.7,则袋子内共有乒乓球__________个。三、解下列各题(本大题共8小题,共72分)17.(8分)如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=1.射线BD为∠ABC的平分线,交AC于点D.动点P以每秒2个单位长度的速度从点B向终点C运动.作PE⊥BC交射线BD于点E.以PE为边向右作正方形PEFG.正方形PEFG与△BDC重叠部分图形的面积为S.
16.在一个不透明的袋子里装有3个白色乒乓球和若干个黄色乒乓球,若从这个袋子里随机摸出一个乒乓球,恰好是黄球的概率为0.7,则袋子内共有乒乓球__________个。三、解下列各题(本大题共8小题,共72分)17.(8分)如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=1.射线BD为∠ABC的平分线,交AC于点D.动点P以每秒2个单位长度的速度从点B向终点C运动.作PE⊥BC交射线BD于点E.以PE为边向右作正方形PEFG.正方形PEFG与△BDC重叠部分图形的面积为S.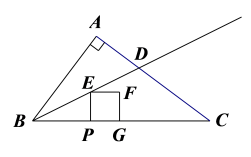 (1)求tan∠ABD的值.(2)当点F落在AC边上时,求t的值.(3)当正方形PEFG与△BDC重叠部分图形不是三角形时,求S与t之间的函数关系式. 18.(8分)某校为了解“阳光体育”活动的开展情况,从全校2000名学生中,随机抽取部分学生进行问卷调查(每名学生只能填写一项自己喜欢的活动项目),并将调查结果绘制成如下两幅不完整的统计图.
(1)求tan∠ABD的值.(2)当点F落在AC边上时,求t的值.(3)当正方形PEFG与△BDC重叠部分图形不是三角形时,求S与t之间的函数关系式. 18.(8分)某校为了解“阳光体育”活动的开展情况,从全校2000名学生中,随机抽取部分学生进行问卷调查(每名学生只能填写一项自己喜欢的活动项目),并将调查结果绘制成如下两幅不完整的统计图.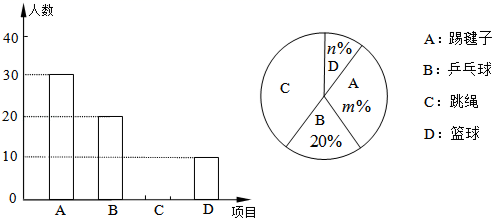 根据以上信息,解答下列问题:(1)被调查的学生共有 人,并补全条形统计图;(2)在扇形统计图中,m= ,n= ,表示区域C的圆心角为 度;(3)全校学生中喜欢篮球的人数大约有多少? 19.(8分)有红、白、蓝三种颜色的小球各一个,它们除颜色外没有其他任何区别.现将3个小球放入编号为①②③的三个盘子里,规定每个盒子里放一个,且只能放一个小球(1)请用树状图或其他适当的形式列举出3个小球放入盒子的所有可能情况;(2)求红球恰好被放入②号盒子的概率. 20.(8分)已知y-2与x+3成正比例,且当x=-4时,y=0,求当x=-1时,y的值. 21.(8分)已知关于
根据以上信息,解答下列问题:(1)被调查的学生共有 人,并补全条形统计图;(2)在扇形统计图中,m= ,n= ,表示区域C的圆心角为 度;(3)全校学生中喜欢篮球的人数大约有多少? 19.(8分)有红、白、蓝三种颜色的小球各一个,它们除颜色外没有其他任何区别.现将3个小球放入编号为①②③的三个盘子里,规定每个盒子里放一个,且只能放一个小球(1)请用树状图或其他适当的形式列举出3个小球放入盒子的所有可能情况;(2)求红球恰好被放入②号盒子的概率. 20.(8分)已知y-2与x+3成正比例,且当x=-4时,y=0,求当x=-1时,y的值. 21.(8分)已知关于![]() 的一元二次方程
的一元二次方程![]() .(1)求证:方程总有两个实数根;(2)若方程两个根的绝对值相等,求此时
.(1)求证:方程总有两个实数根;(2)若方程两个根的绝对值相等,求此时![]() 的值. 22.(10分)数学问题:用边长相等的正三角形、正方形和正六边形能否进行平面图形的镶嵌?问题探究:为了解决上述数学问题,我们采用分类讨论的思想方法去进行探究.探究一:从正三角形、正方形和正六边形中任选一种图形,能否进行平面图形的镶嵌?第一类:选正三角形.因为正三角形的每一个内角是60°,所以在镶嵌平面时,围绕某一点有6个正三角形的内角可以拼成一个周角,所以用正三角形可以进行平面图形的镶嵌.第二类:选正方形.因为正方形的每一个内角是90°,所以在镶嵌平面时,围绕某一点有4个正方形的内角可以拼成一个周角,所以用正方形也可以进行平面图形的镶嵌.第三类:选正六边形.(仿照上述方法,写出探究过程及结论)探究二:从正三角形、正方形和正六边形中任选两种图形,能否进行平面图形的镶嵌?第四类:选正三角形和正方形在镶嵌平面时,设围绕某一点有x个正三角形和y个正方形的内角可以拼成个周角.根据题意,可得方程60x+90y=360整理,得2x+3y=1.我们可以找到唯一组适合方程的正整数解为
的值. 22.(10分)数学问题:用边长相等的正三角形、正方形和正六边形能否进行平面图形的镶嵌?问题探究:为了解决上述数学问题,我们采用分类讨论的思想方法去进行探究.探究一:从正三角形、正方形和正六边形中任选一种图形,能否进行平面图形的镶嵌?第一类:选正三角形.因为正三角形的每一个内角是60°,所以在镶嵌平面时,围绕某一点有6个正三角形的内角可以拼成一个周角,所以用正三角形可以进行平面图形的镶嵌.第二类:选正方形.因为正方形的每一个内角是90°,所以在镶嵌平面时,围绕某一点有4个正方形的内角可以拼成一个周角,所以用正方形也可以进行平面图形的镶嵌.第三类:选正六边形.(仿照上述方法,写出探究过程及结论)探究二:从正三角形、正方形和正六边形中任选两种图形,能否进行平面图形的镶嵌?第四类:选正三角形和正方形在镶嵌平面时,设围绕某一点有x个正三角形和y个正方形的内角可以拼成个周角.根据题意,可得方程60x+90y=360整理,得2x+3y=1.我们可以找到唯一组适合方程的正整数解为![]() .镶嵌平面时,在一个顶点周围围绕着3个正三角形和2个正方形的内角可以拼成一个周角,所以用正三角形和正方形可以进行平面镶嵌第五类:选正三角形和正六边形.(仿照上述方法,写出探究过程及结论)第六类:选正方形和正六边形,(不写探究过程,只写出结论)探究三:用正三角形、正方形和正六边形三种图形是否可以镶嵌平面?第七类:选正三角形、正方形和正六边形三种图形.(不写探究过程,只写结论), 23.(10分)解方程(1)
.镶嵌平面时,在一个顶点周围围绕着3个正三角形和2个正方形的内角可以拼成一个周角,所以用正三角形和正方形可以进行平面镶嵌第五类:选正三角形和正六边形.(仿照上述方法,写出探究过程及结论)第六类:选正方形和正六边形,(不写探究过程,只写出结论)探究三:用正三角形、正方形和正六边形三种图形是否可以镶嵌平面?第七类:选正三角形、正方形和正六边形三种图形.(不写探究过程,只写结论), 23.(10分)解方程(1)![]() (2) x(3-2x)= 4 x-6 24.(12分)如图,在四边形纸片ABCD中,∠B=∠D=90°,点E,F分别在边BC,CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都和点G重合,∠EAF=45°.(1)求证:四边形ABCD是正方形;(2)求证:三角形ECF的周长是四边形ABCD周长的一半;(3)若EC=FC=1,求AB的长度.
(2) x(3-2x)= 4 x-6 24.(12分)如图,在四边形纸片ABCD中,∠B=∠D=90°,点E,F分别在边BC,CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都和点G重合,∠EAF=45°.(1)求证:四边形ABCD是正方形;(2)求证:三角形ECF的周长是四边形ABCD周长的一半;(3)若EC=FC=1,求AB的长度.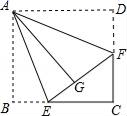 参考答案 一、选择题(每小题3分,共30分)1、C2、A3、A4、B5、A6、D7、B8、C9、B10、A 二、填空题(本大题共有6小题,每小题3分,共18分)11、-112、(2,-1)13、314、1.239×10-3.15、116、10 三、解下列各题(本大题共8小题,共72分)17、(1)tan∠ABD=
参考答案 一、选择题(每小题3分,共30分)1、C2、A3、A4、B5、A6、D7、B8、C9、B10、A 二、填空题(本大题共有6小题,每小题3分,共18分)11、-112、(2,-1)13、314、1.239×10-3.15、116、10 三、解下列各题(本大题共8小题,共72分)17、(1)tan∠ABD=![]() ;(2)
;(2)![]() ;(3)①当
;(3)①当![]() 时,
时,![]() ;②当
;②当![]() 时,
时,![]() ;③当
;③当![]() 时,
时,![]() .18、(1)学生总数100人,跳绳40人,条形统计图见解析;(2)144°;(3)200人.19、(1)详见解析;(2)
.18、(1)学生总数100人,跳绳40人,条形统计图见解析;(2)144°;(3)200人.19、(1)详见解析;(2)![]() 20、2.21、(1)见解析;(2)
20、2.21、(1)见解析;(2)![]() 或-1.22、详见解析23、 (1)
或-1.22、详见解析23、 (1) ![]() ;(2)
;(2) ![]() .24、(1)见解析;(2)见解析;(3)
.24、(1)见解析;(2)见解析;(3)![]() +1
+1
相关试卷
这是一份2023-2024学年上海市浦东新区第四教育署数学九上期末联考试题含答案,共8页。试卷主要包含了如图,的直径,弦于,已知二次函数y=,在中,=90〫,,则的值是等内容,欢迎下载使用。
这是一份2023-2024学年上海市浦东新区第一教育署九上数学期末检测模拟试题含答案,共8页。试卷主要包含了下图中,不是中心对称图形的是,抛物线,下列说法正确的是等内容,欢迎下载使用。
这是一份上海市浦东新区第四教育署2023-2024学年数学八上期末质量检测试题含答案,共7页。试卷主要包含了当x=-1时,代数式的结果是,如图所示,C为线段AE上一动点,点关于x轴对称的点的坐标为,已知是多项式的一个因式,则可为等内容,欢迎下载使用。









