湘教版（2019）必修 第二册3.3 复数的几何表示优质教学设计

《3.3复数的几何表示》教学设计

一、课程标准

理解复数的几何意义，会求复数的模；掌握共轭复数的概念，会求一个复数的共轭复数.

二、教学目标

1.类比实数的几何意义学习复数的几何意义，类比向量的模长和加减法的几何意义学习复数的模长及加减法的几何意义；

2.理解复数的模长与共轭复数的概念，会求复数的模长及共轭复数.

三、重点重点：复数的模与共轭复数，复数的几何意义.

四、教学难点：复数的几何意义及其复数加减法的几何意义.

五、教学过程

（一）创设情境，引入新课

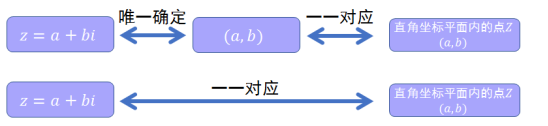
1.实数都与数轴上的点一一对应，那复数应该与什么建立一一对应的联系呢？

2.复数如何确定？         

（二）自主学习，熟悉概念

1.要求：学生阅读P109-112

2.思考：

（1）什么是复平面、实轴、虚轴？.

（2）复数的几何意义是什么？

（3）什么是复数的模？

（4）什么是共轭复数？

（5）复数的加减法的几何意义是什么？

（三）   检验自学，强化概念

1. 复平面、实轴、虚轴：
2. 复数的几何意义：

3.复数的模：复数z=(a,b∈R) 在复平面上所对应的向量的模称为复数z的模，也称为z的绝对值，记作|z|。写成公式，即||=

|z|=表示点(a,b)到原点的距离。

4.共轭复数：复数称为z=(a,b∈R)共轭复数，记为。即=,反过来也有=，因此=z.

5.复数加减法的几何意义

如图所示，设复数，(a,b,c,d∈R)分别对应向量、，则=(a,b), =(c,d).由平面向量坐标运算得，+=(a+c)+(b+d)i就对应向量

=(a+c,b+d)= +,且OS是以OP、OQ为邻边的平行四边形的对角线，即复数的加法由对应向量、加法来表示，且复数加法几何意义就是向量加法的平行四边形法则。

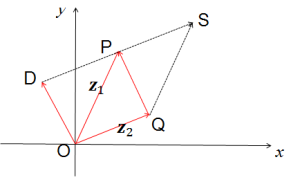
类似地，复数的减法由对应向量的减法来表示,其几何意义就是向量减法的三角形法则。

实数k与复数z相乘就可由实数k与该复数所对应的向量OP的数乘来表示。

6.例题讲解

例1.在复平面上画出以下复数分别对应的点

（1）求向量的模.

（2）点中是否存在两个点关于实轴对称？若存在，则它们所对应的复数有什么关系？

设计意图：让学生深入地理解复数的几何意义，理解复数的模的概念.

例2.分别求复数和的共轭复数，并分别比较与，与的大小.

设计意图：理解共轭复数、模的概念，能进行复数的运算.

例3. 设，点对应的复数，在复平面内满足下列条件的点的集合是什么图像？

设计意图：让学生深入地理解复数的几何意义.

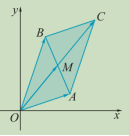例4. 如图，已知复平面上的平行四边形，是原点，分别对应的复数，是的交点，求点对应的复数.

设计意图：让学生深入地理解复数的几何意义，会进行复数的运算。

(三)课堂练习及检测

P113    1,2,3，4

(四)归纳小结

1.复数的几何意义：

2.复数的模：

3.共轭复数：

4.复数加减法的几何意义

（五）作业

1.习题3.3  1,2,3,4,5

2.预习3.4复数的三角表示

六、教学反思（酌情写一些）

七、板书设计