


【同步练习】北师大版数学六年级上册--1.1圆的认识(一)练习(含答案)
展开
![]()
一、学习重难点
1、学习重点:理解圆的特征,会用圆规画圆。
2、学习难点:体会圆心和半径的作用。
二、知识梳理
1、圆的认识。
圆是由一条曲线围成的封闭图形,圆上任意一点到圆心的距离都相等。
2、圆的画法。
(1)手指画圆法。(2)实物画圆法。(3)系绳画圆法。(4)圆规画圆法(要求十分精确的情况下用圆规画圆)。
3、圆的各部分名称。
(1)圆心。画圆时,圆规带有针尖的脚所在的点叫圆心。
圆心一般用字母O表示。
(2)半径。用圆规画圆时,圆规两脚之间的距离就是所画圆的半径,即圆心到圆上任意一点的距离叫半径。
半径一般用字母r表示。
(3)直径。通过圆心并且两端都在圆上的线段叫作直径。直径一般用字母d表示。
4、圆的各部分之间的关系。
圆有无数条直径,无数条半径;同圆(或等圆)中的直径都相等,半径都相等;直径的长度是半径的2倍,可以表示为d=2r或r=。
5、圆心和半径的作用:圆心确定圆的位置,半径决定圆的大小。

一、选择题
1.(2022·福建莆田·统考小升初真题)用如图的方法可以测量没有标出圆心的圆的直径,这是因为( )。
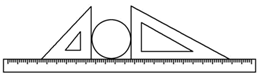
A.圆是轴对称图形
B.直径长度是半径的2倍
C.两端都在圆上的线段中,直径最长
D.圆心确定了,圆的中心位置就确定了
2.(2021·河北保定·统考小升初真题)一个圆的圆上有两点,这两点之间的距离是8cm,那么这个圆的半径( )。
A.等于4cm B.大于或等于4cm C.小于4cm
3.(2023秋·山西吕梁·六年级统考期末)车轮制作成圆形是因为( )。
A.同一个圆的半径是相等的 B.圆滚动一周的长度是直径的π倍 C.以上说法都不对
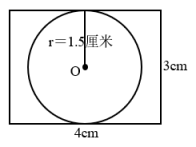
4.(2022秋·陕西渭南·六年级统考期末)如图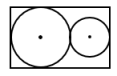 ,长方形的长是5厘米,宽是3厘米,则小圆的半径是( )厘米。
,长方形的长是5厘米,宽是3厘米,则小圆的半径是( )厘米。
A.1.5 B.2 C.1 D.0.5
5.(2022秋·吉林长春·六年级统考期末)下面图形分别在平面上滚动,中心点留下的痕迹是一条直线的是( )。
A. B.
B. C.
C.
二、填空题
6.(2023秋·广东揭阳·六年级统考期末)通过圆心,并且两端都在圆上的线段叫做( ),同一个圆内,直径的长度是半径长度的( )。
7.(2022秋·陕西咸阳·六年级统考期末)如图,其中一个圆的直径是( )cm,半径是( )cm,长方形的长是( )cm。

8.(2023秋·海南省直辖县级单位·六年级统考期末)( )决定圆的大小,( )决定圆的位置。
9.(2021秋·四川成都·六年级统考期末)在套圈游戏中,站成圆形比方形更公平,因为在同一个圆内,圆心到圆上任意一点的距离都( )。
10.(2023秋·广东深圳·六年级统考期末)龙龙老师需要用一些半径为1.5厘米的圆形纸片来装饰班级文化墙。如果在一张长22厘米、宽15厘米的长方形纸上剪这样的圆,最多能剪( )个。

三、作图题
11.(2022秋·广东深圳·六年级统考期末)按要求画图。
(1)画一个长4cm,宽3cm的长方形。
(2)在这个长方形内画一个最大的圆,并用![]() 标注出圆心。
标注出圆心。
(3)在这个圆中画一条半径,并标注出半径的长度。
四、解答题
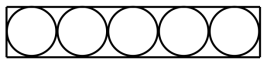
12.(2021秋·浙江·四年级期中)如下图盒子内正好放下5瓶罐头,每瓶罐头的瓶底的半径是3厘米,则这个盒子的长是多少厘米?
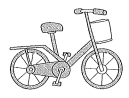
13.(2022秋·六年级单元测试)妈妈的自行车运行不平稳了,找修车师傅后,修车师傅调整了车轮上车条的长度。你知道这是为什么吗?
14.(2022秋·辽宁大连·六年级统考期末)画一个直径4cm的圆,用0、r标注圆心和半径;在这个圆内画一个最大的正方形,正方形的面积是( )cm2。
参考答案
1.C
【分析】根据直径的含义:通过圆心并且两端都在圆上的线段叫做直径,在圆中直径最长;由此解答即可。
【详解】A.圆是轴对称图形,与本题测量圆的直径无关;
B.直径长度是半径的2倍,与本题测量圆的直径无关;
C.两端都在圆上的线段中,直径最长,根据直径的含义可知:直径是圆内最长的线段,两端都在圆上的线段中,直径最长。故此选项符合题意;
D.圆心确定了,圆的中心位置就确定了,与本题测量圆的直径无关;
故答案为:C。
【分析】此题考查了圆的认识与圆周率,明确直径的含义,是解答此题的关键。
2.B
【分析】如果这两点之间的线段是直径时,半径就是4厘米;如果这两点之间的线段不是直径时,半径就要大于4厘米;由此即可解答。
【详解】8÷2=4(厘米)
由分析可知:圆的半径可能等于4厘米或者大于4厘米。
故选:B。
【分析】本题主要考查圆的认识,要注意在一个圆中,直径是最长的线段。
3.A
【分析】车轮制成圆形是为了行驶的时候平稳,并且易滚动,是利用了同一个圆内半径都相等的原理设计的,据此解答。
【详解】车轮设计成圆形,是因为同一圆内所有半径都相等。
故答案为:A
【分析】本题考查了圆在生活中的应用。
4.C
【分析】根据图形可知,大圆直径等于长方形的宽,大圆直径+小圆直径=长方形的长,由此求出小圆直径,进而求出小圆半径。
【详解】(5-3)÷2
=2÷2
=1(厘米)
如图 ,长方形的长是5厘米,宽是3厘米,则小圆的半径是1厘米。
,长方形的长是5厘米,宽是3厘米,则小圆的半径是1厘米。
故答案为:C
【分析】明确大圆的直径等于长方形的宽,小圆的直径等于长方形的长减去大圆直径的差,是解答此题的关键。
5.C
【分析】图形在平面上滚动,要使中心点留下的痕迹是一条直线,则中心点到图形上任意一点的距离都相等,据此解答。
【详解】A.正方形的中心点到正方形上任意一点的距离不一定相等,则中心点留下的痕迹不是一条直线,如下图所示:
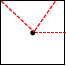 ;
;
B.椭圆的中心点到椭圆上任意一点的距离不一定相等,则中心点留下的痕迹不是一条直线,如下图所示:
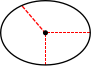 ;
;
C.圆的中心点到圆上任意一点的距离都相等,即同一个圆的半径都相等,则中心点留下的痕迹是一条直线,如下图所示:
 。
。
故答案为:C
【分析】同一个圆的半径都相等,则圆滚动时,圆心留下的痕迹是一条直线,
6.直径 2倍
【详解】通过圆心,并且两端都在圆上的线段叫做直径,同一个圆内,直径的长度是半径长度的2倍。
如图:
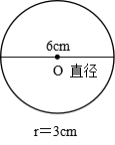
7.6 3 9
【分析】根据题意,其中一个圆的直径是6cm,半径是圆的直径的一半,是3cm,长方形的长是一个直径的长度加一个半径的长度,据此解答即可。
【详解】6÷2=3(cm)
3+6=9(cm)
即一个圆的直径是6cm,半径是3cm,长方形的长是9cm。
【分析】本题考查了圆的认识,结合题意分析解答即可。
8.半径 圆心
【分析】圆是一种几何图形.当一条线段绕着它的一个端点在平面内旋转一周时,它的另一个端点的轨迹叫做圆,这一个点叫做圆心,决定圆的位置,半径决定圆的大小。据此解答即可。
【详解】半径决定圆的大小,圆心决定圆的位置。
【分析】本题考查了圆的认识。
9.相等
【分析】连接圆心和圆上任意一点的线段是半径,同一个圆里,有无数条半径,所有半径长度都相等;据此解答。
【详解】由分析可得:在同一个圆内,圆心到圆上任意一点的距离是圆的半径,所以圆心到圆上任意一点的距离都相等。
【分析】本题主要考查圆的特征。
10.35
【分析】长方形的长和宽分别包含几个圆的直径,再相乘即可。
【详解】22÷(1.5×2)×[15÷(1.5×2)]
=22÷3×[15÷3]
≈7×5
=35(个)
最多能剪35个。
【分析】本题主要考查图形拼组,关键是注意求长方形长和宽分别包含几个圆的直径。
11.(1)、(2)、(3)见详解
【分析】(1)根据画指定长方形的长和宽的方法画图即可;
(2)长方形内画一个最大的圆,则圆的直径等于长方形的宽,画圆的步骤:把圆规的两脚分开,定好两脚的距离,即半径;把有针尖的一只脚固定在一点上,即圆心;把装有铅笔尖的一只脚旋转一周,就画出一个圆。在圆心处标注O即可。
(3)圆心到圆上的距离是半径,半径等于长方形宽的一半,据此即可标出对应的数据。
【详解】(1)(2)(3)如下图所示:
【分析】关键是掌握画长方形和圆的方法,同时要清楚圆的特征是解题的关键。
12.30厘米
【分析】根据题意可知,每瓶罐头瓶底的直径为3×2=6厘米,这个盒子的长为5个直径的长度,即5×6=30厘米,据此解答即可。
【详解】![]()
=6×5
=30(厘米)
答:这个盒子的长是30厘米。
【分析】明确盒子的长为5个直径的长度是解答本题的关键。
13.见详解
【分析】依据是在同圆中,所有的半径都相等;使车条一样长,这样车轮就成为一个圆,可以平稳运行。
【详解】答:因为连接圆心到圆上任意一点的线段叫做半径,在同圆中,所有的半径都相等;自行车运行不平稳时,修车师傅常常要调整车轮上车条的长度,使车条一样长,这样车轮就成为一个圆,可以平稳运行。
【分析】此题主要根据圆的概念和特点来解释生活中的问题。
14.图见详解;8
【分析】以O为圆心,直径为4cm,则半径为4÷2=2cm,画出符合要求的圆;再以两条互相垂直的直径为对角线,即可画出要求的正方形;直径已知,则正方形的对角线的长度已知,进而求出正方形的面积。
【详解】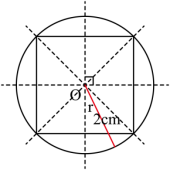
正方形面积:4×(4÷2)÷2×2
=4×2÷2×2
=8÷2×2
=4×2
=8(cm2)
【分析】本题考查画圆,以及圆内画正方形,以及正方形面积公式的应用。











