【单元教案】北师大版数学六年级上册-第一单元 《圆的面积（二）》（教案）

《圆的面积（二）》教学简案

【教学内容】

北师大版六年级上册第一单元第9课时

【教学目标】

1.能正确运用圆的面积公式计算圆的面积，并能解决一些简单的实际问题。

2.在多个探究圆面积公式的活动中、体会圆的半径、周长、面积之间的关系。

3.结合剪杯垫的活动，进一步丰富学生探索圆面积公式的方法，并体会“等积变形”的数学思想。

【教学重、难点】

教学重点：圆面积公式的应用。

教学难点：圆周长与面积的综合应用。

【教学准备】

ppt课件

【教学过程】

一、创设情境，引出问题。

1.呈现农田及牧场的情境图，引导学生观察。

2.观察旋转喷水器，得到喷水头转动一周，浇灌农田的形状就是圆。

3.提出问题：喷水头转动一周，能浇灌多大面积的农田？

二、解决问题，探索新知。

问题1：喷水头转动一周，能浇灌多大面积的农田？

1.学生独立尝试运用公式计算面积。

2.交流反馈。

因为，所以可以用3.14×（3×3），结果是28.26平方米。

3.优化半径的平方的表达方式。

“3的平方”可以写成“3²”。

4.观察羊圈，引出新的问题。

问题2：量的圆形羊圈的周长是125.6米。羊圈的面积是多少平方米？

1.学生独立尝试运用公式解决问题。

2.交流反馈学生的解答过程。

要求圆的面积要先知道圆的半径。因为C=2?r,所以可以反过来用125.6÷3.14÷2算出半径，是20米；再利用圆面积的计算公式S=?r²，也就是3.14×20²算出这个羊圈的面积是1256平方米。

3.引导学生进一步梳理和反思：为什么要先求圆的半径？求圆的半径列式计算的根据是什么？根据求圆的半径所列的算式，怎样计算更合理和简捷？

问题3：圆的面积公式是如何推导出来的？

1.给出借助剪杯垫推导圆面积的方法。

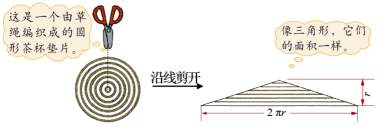
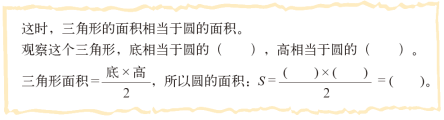
2.学生独立阅读并尝试完成填空。

3.交流反馈。

4.引导反思。

这种推导圆面积的方法的关键是什么？草绳覆盖的面积的形状变了，但所覆盖的图形的面积不变。

三、练习应用，巩固提升。

1．一个圆形杯垫的半径是4cm，这个杯垫的面积是多少平方厘米？

2. 有一圆形蓄水池。它的周长是31.4m，它的占地面积约是多少？

3. 一个运动场跑道的形状与大小如图。两边是半圆形，中间是长方形，

   这个运动场的占地面积是多少？

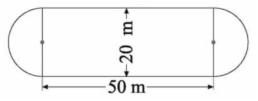
4.拓展练习。

（1）如上图，这个运动场的周长是多少？（2）同一个运动场，在计算它的面积和周长时有什么不同？

四、全课回顾，总结收获

回顾本课重点研究的三个问题，进一步梳理和总结本课学习的收获。