数学七年级上册1.2 展开与折叠优质导学案

这是一份数学七年级上册1.2 展开与折叠优质导学案，共7页。

2 展开与折叠
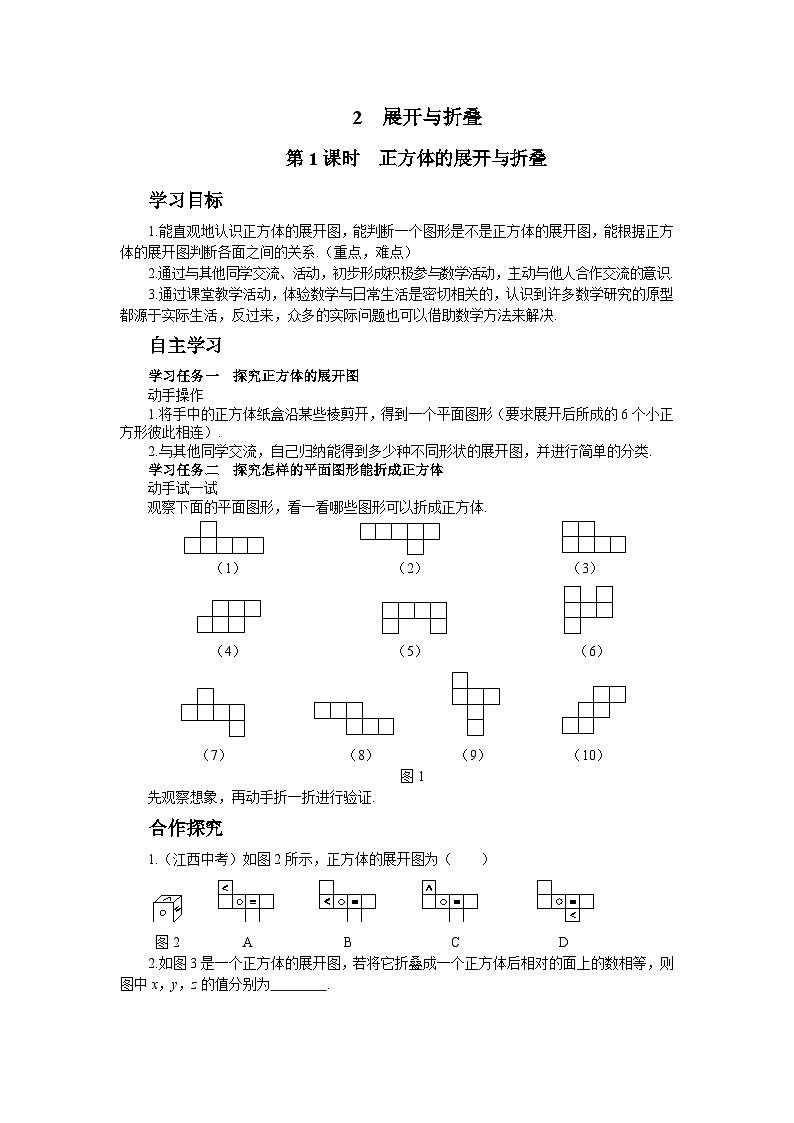
第1课时　正方体的展开与折叠
学习目标
1.能直观地认识正方体的展开图，能判断一个图形是不是正方体的展开图，能根据正方体的展开图判断各面之间的关系.（重点，难点）
2.通过与其他同学交流、活动，初步形成积极参与数学活动，主动与他人合作交流的意识.
3.通过课堂教学活动，体验数学与日常生活是密切相关的，认识到许多数学研究的原型都源于实际生活，反过来，众多的实际问题也可以借助数学方法来解决.
自主学习
学习任务一　探究正方体的展开图
动手操作
1.将手中的正方体纸盒沿某些棱剪开，得到一个平面图形（要求展开后所成的6个小正方形彼此相连）.
2.与其他同学交流，自己归纳能得到多少种不同形状的展开图，并进行简单的分类.
学习任务二　探究怎样的平面图形能折成正方体
动手试一试
观察下面的平面图形，看一看哪些图形可以折成正方体.

（1） （2） （3）

（4） （5） （6）

（7） （8） （9） （10）
图1
先观察想象，再动手折一折进行验证.
合作探究
1.（江西中考）如图2所示，正方体的展开图为（　　）
       
图2 A　　 B　　 C　　 D
2.如图3是一个正方体的展开图，若将它折叠成一个正方体后相对的面上的数相等，则图中x，y，z的值分别为　　　　.

图3
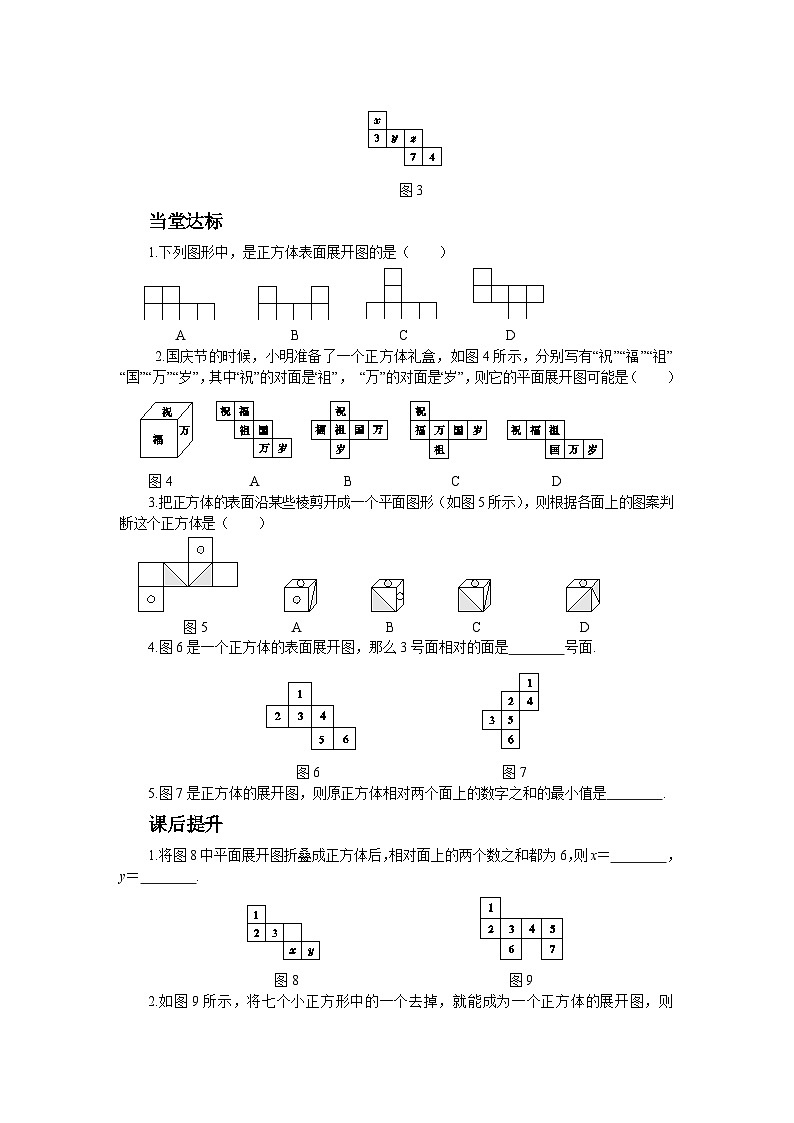
当堂达标
1.下列图形中，是正方体表面展开图的是（　　）
　    
A B C　 D
2.国庆节的时候，小明准备了一个正方体礼盒，如图4所示，分别写有“祝”“福”“祖” “国”“万”“岁”，其中“祝”的对面是“祖”， “万”的对面是“岁”，则它的平面展开图可能是（　　）
 　 　
图4 A B C D
3.把正方体的表面沿某些棱剪开成一个平面图形（如图5所示），则根据各面上的图案判断这个正方体是（　　）
  　 　 　
图5 A 　B C 　D
4.图6是一个正方体的表面展开图，那么3号面相对的面是　　　　号面.

图6           图7
5.图7是正方体的展开图，则原正方体相对两个面上的数字之和的最小值是　　　　.
课后提升
1.将图8中平面展开图折叠成正方体后，相对面上的两个数之和都为6，则x＝　　　　，y＝　　　　.

图8 图9
2.如图9所示，将七个小正方形中的一个去掉，就能成为一个正方体的展开图，则去掉的小正方形的序号是　　　　或　　　　.
3.图10是一个几何体的展开图，每个面上都标有相应的字母.
（1）若A面在几何体的底部，则上面是哪一面？
（2）若F面在前面，B面在左面，则上面是哪一面？
（3）若C面在右面，D面在后面，则上面是哪一面？

图10



























反思感悟
我的收获：

我的易错点：


参考答案
自主学习
学习任务一
1.得到的平面图形有以下情形如图11所示：
    
（1） （2） （3） （4） （5） （6）

（7） （8） （9） （10） （11）
图11
2.可分为四类：
（1）如图12所示，一四一型（共6种），四个一行中排列，两端各一个任意放.
  
（1） （2） （3） （4） （5） （6）
图12
（2）如图13所示，二三一型（共3种），二在三上露一端，一在三下任意放.

（1） （2） （3）
图13
（3）如图14所示，二二二型（1种），两两三行排有序，恰似登天上云梯.

图14 图15
（4）如图15所示，三三型（1种），三个三个排两行，中间一“日”放光芒.
学习任务二
（7）（8）（9）（10）可以折叠成正方体.
合作探究
1.A 2.7，4，3
当堂达标
1.D 2.C 3.C 4.6 5.6
课后提升
1.5 3 2.6 7
3.解：（1）F面；（2）E面或C面；（3）A面或F面.


2 展开与折叠
第2课时　其他几何体的展开与折叠
学习目标
1.能直观地认识棱柱的展开图，了解圆柱、圆锥的侧面展开图的形状.（重点）
2.根据几何体的展开图正确判断一个平面图形能围成什么样的几何体，能制作简单的几何体模型.（难点）
3.通过展开与折叠的实践操作，经历和体验图形的转换过程，发展空间观念.
自主学习
学习任务一　探究棱柱的展开图
准备如图1所示的棱柱纸质模型，将图1中棱柱的纸质模型沿某些棱展开，观察得到的平面图形的形状，并与其他同学交流你的剪开方法和展开图的形状.

（1） （2） （3）
图1
学习任务二　探究圆柱、圆锥的侧面展开图
准备如图2所示的圆柱和圆锥的纸筒，按照图2所示的方法把圆柱和圆锥的侧面展开，观察得到的平面图形的形状，完成下面的填空.
圆柱的侧面展开图是　　　　，圆锥的侧面展开图是　　　　.

图2
合作探究
（1）如图3所示，下列哪些图形经过折叠可以围成一个棱柱？先想一想，再折一折.

（1） （2） （3） （4）
图3
（2）将图3中不能围成棱柱的图形作适当修改使得图形能围成一个棱柱.
当堂达标
1.下面形状的四张纸板，可以围成一个三棱柱的是（　　）
　    　
A　 B C D
2.下面图形经过折叠不能围成棱柱的是（　　）
　     　  
A B C 　D
3.（湖南益阳中考）下列几何体中，其侧面展开图为扇形的是（　　）
　  　   　 
A　 B　 C 　 D
4.图4是一个长方体包装盒，则它的表面展开图是（　　）
    　　 　
图4　 A　　 　 B　 　　 C　 　　 D
5.一个底面为正方形的直棱柱的侧面展开图是边长为12的正方形，则它的表面积为　　　　.
课后提升
图5是一个棱柱形状的食品包装盒的表面展开图.
（1）请写出这个包装盒的多面体形状的名称.
（2）根据图中所标的尺寸，计算这个多面体的侧面积.

图5



反思感悟
我的收获：

我的易错点：

参考答案
自主学习
学习任务一：学生自己动手操作.
学习任务二：学生自己动手操作，长方形，扇形.
合作探究
（1）第（2）（4）个图形经过折叠可以围成一个棱柱.
（2）答案不唯一，
如：第（1）个图形修改为；
第（3）个图形修改为.
当堂达标
1.B　解析：三棱柱的展开图中，侧面展开是3个长方形，上下底面是2个三角形.
2.D　解析：A围成四棱柱，B围成五棱柱，C围成三棱柱，D的侧面展开图是3个长方形，而底面却是两个四边形，对应的侧面数和底面的边数不同，不能围成棱柱.
3.C　解析：A.圆柱的侧面展开图是长方形；
B.三棱柱的侧面展开图不是扇形；
C.圆锥的侧面展开图是扇形；
D.三棱锥的侧面展开图不是扇形.
故选C.
4.A　解析：根据四棱柱的四个侧面和上下两个底面的特征可知，A项可以拼成一个长方体，B，C，D项均不符合长方体的展开图的特征，故不是长方体的展开图.故选A.
5.162　解析：直棱柱的底面正方形的边长为12÷4＝3，高为12，
则它的表面积为3×3×2+12×3×4＝18+144＝162.
课后提升
解：（1）共有3个长方形组成侧面，2个三角形组成底面，故是三棱柱.
（2）因为AB＝5，AD＝3，BE＝4，DF＝6，
所以侧面积为3×6+5×6+4×6＝18+30+24＝72.