2022-2023学年浙江省绍兴市嵊州市三界片八年级（下）期中数学试卷（含解析）

这是一份2022-2023学年浙江省绍兴市嵊州市三界片八年级（下）期中数学试卷（含解析），共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2022-2023学年浙江省绍兴市嵊州市三界片八年级（下）期中数学试卷
一、选择题（本大题共10小题，共20.0分。在每小题列出的选项中，选出符合题目的一项）
1. 下列图形中，既是轴对称图形又是中心对称图形的是(    )
A. B. C. D.
2. 下列方程中是一元二次方程的是(    )
A. 2x−1=0 B. 3x+x=5 C. x+y=6 D. x2−2x−3=0
3. 甲、乙两班分别有10名选手参加体操比赛，两班参赛选手身高的方差分别是S甲2=1.5cm2，S乙2=2.5cm2，则下列说法正确的是(    )
A. 甲班选手的身高比乙班选手的整齐 B. 乙班选手的身高比甲班选手的整齐
C. 甲、乙两班选手的身高一样整齐 D. 无法确定哪班选手的身高整齐
4. 用反证法证明：“一个三角形中至多有一个钝角”时，应假设(    )
A. 一个三角形中至少有两个钝角 B. 一个三角形中至多有一个钝角
C. 一个三角形中至少有一个钝角 D. 一个三角形中没有钝角
5. 某药品经过两次降价，每瓶零售价由100元降为81元，设平均每次降价的百分率为x，则下面所列方程正确的是(    )
A. 100(1−x)2=811 B. 100(1−x)2=81
C. 100(1−x%)2=81 D. 100x2=81
6. 若点P(a,3)与Q(−2,b)关于坐标原点对称，则a+b的值为(    )
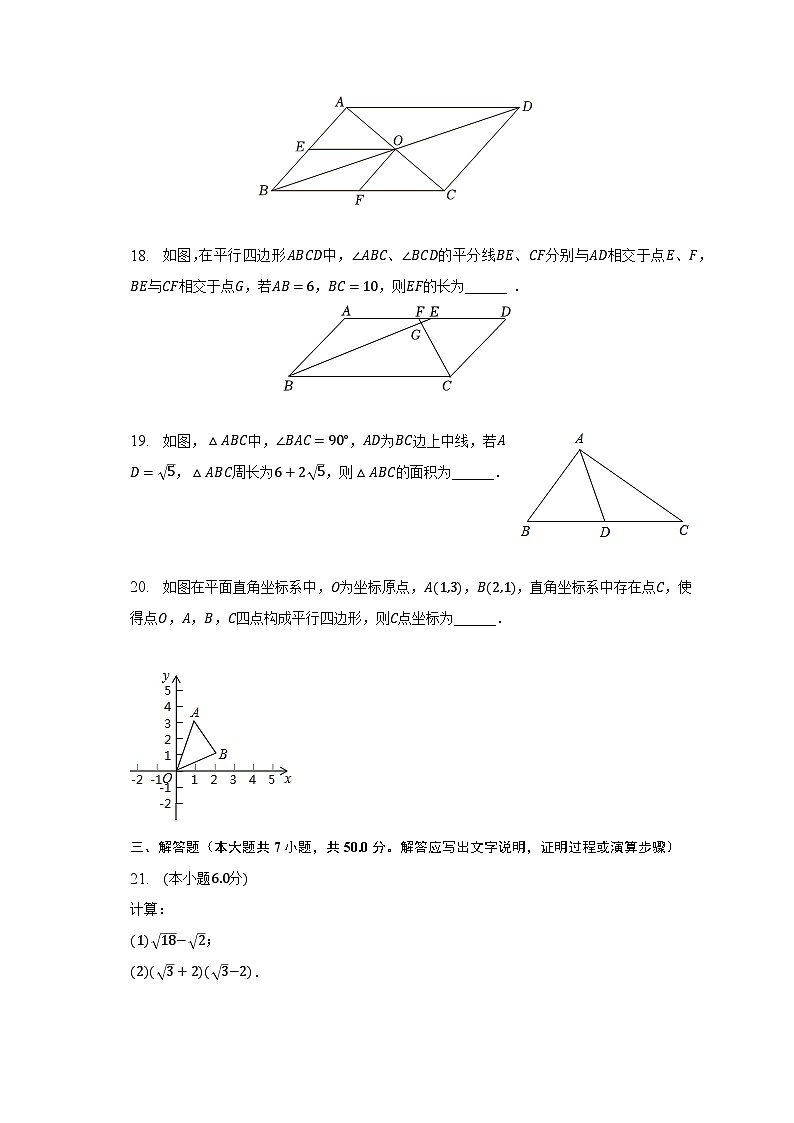
A. 1 B. −1 C. 3 D. −3
7. 已知关于x的一元二次方程kx2−4 2x+2=0有两个不相等的实数根，则k的取值范围是(    )
A. k<4 B. k<4且 k≠0 C. k≥−4且k≠0 D. k≤−4且 k≠0
8. 如图，在四边形ABCD中，对角线AC，BD相交于点O，且OA=OC，OB=OD.下列结论不一定成立的是(    )


A. AD=BC B. AB/​/CD
C. ∠DAB=∠BCD D. ∠DAB=∠ABC
9. 如图，在平行四边形ABCD中，O是对角线AC，BD的交点．已知AB=4，AC=10，△AOB的周长是11.则对角线BD的长为(    )


A. 3 B. 4 C. 5 D. 6
10. 如图，在平行四边形ABCD中，连接BD，且BD=CD，过点A作AM⊥BD于点M，过点D作DN⊥AB于点N，且DN=6，在DB的延长线上取一点P，满足∠ABD=∠MAP+∠PAB，则AP=(    )


A. 8 B. 10 C. 6 2 D. 6 3
二、填空题（本大题共10小题，共30.0分）
11. 若二次根式 3x−6有意义，则x的取值范围是______ ．
12. 若关于x的方程x2+3x−k=0有一个解是1，则k的值是______．
13. 方程x2−4=0的根是          ．
14. 若一个六边形的六个内角都相等，则每个内角的度数为______ ．
15. 如图，在平行四边形ABCD中，∠A+∠C=240°，则∠B= ______ 度．


16. 一组数据2，3，x，5，7的平均数是5，则这组数据的中位数是          ．
17. 如图，在平行四边ABCD中，E，F分别是AB，BC的中点，O是对角线的交点.若OE=4cm，OF=3cm，则平行四边形ABCD的周长为______ ．

18. 如图，在平行四边形ABCD中，∠ABC、∠BCD的平分线BE、CF分别与AD相交于点E、F，BE与CF相交于点G，若AB=6，BC=10，则EF的长为______ ．

19. 如图，△ABC中，∠BAC=90°，AD为BC边上中线，若AD= 5，△ABC周长为6+2 5，则△ABC的面积为______．


20. 如图在平面直角坐标系中，O为坐标原点，A(1,3)，B(2,1)，直角坐标系中存在点C，使得点O，A，B，C四点构成平行四边形，则C点坐标为______．


三、解答题（本大题共7小题，共50.0分。解答应写出文字说明，证明过程或演算步骤）
21. (本小题6.0分)
计算：
(1) 18− 2；
(2)( 3+2)( 3−2)．
22. (本小题6.0分)
用适当的方法解下列方程：
(1)x2−2x−2=0；
(2)(x+1)(x+2)=2x+4．
23. (本小题6.0分)
已知：如图，在四边形ABCD中，点E在BC的延长线上，AD=BC，∠D=∠DCE.求证：四边形ABCD是平行四边形．

24. (本小题6.0分)
下列3×3网格图都是由9个相同的小正方形组成，每个网格图中有3个小正方形已涂上阴影，请在余下的6个空白小正方形中，按下列要求涂上阴影：

(1)选取1个涂上阴影，使4个阴影小正方形组成一个轴对称图形，但不是中心对称图形．
(2)选取1个涂上阴影，使4个阴影小正方形组成一个中心对称图形，但不是轴对称图形．
(3)选取2个涂上阴影，使5个阴影小正方形组成既是一个中心对称图形，又是轴对称图形．
25. (本小题8.0分)
已知：如图，AC，BD是▱ABCD的两条对角线，AE⊥BD，CF⊥BD，垂足分别为E，F.求证：EO=FO．

26. (本小题8.0分)
“夹菜用公筷，健康千万家”某商店为响应“公筷行动”，批发销售一批公筷.每双公筷的成本为8元，当销售单价为10元时，每天能售出200双.后来经过市场调查发现，若销售单价每涨1元，则每天的销售量减少20双，设销售单价为x元．
(1)当x为11时，每天可售出______ 双.
(2)每双的盈利为______ 元，每天的销售量为______ 双.(用含x的代数式表示)
(3)若该商店需要保证每天盈利640元，同时又要使顾客得到实惠，那么销售单价应该定为多少元？
27. (本小题10.0分)
如图①，在矩形ABCD中，AB=8，AD=4.点P从点A出发，沿A→D→C→D运动，速度为每秒2个单位长度；点Q从点A出发向点B运动，速度为每秒1个单位长度．P、Q两点同时出发，点Q运动到点B时，两点同时停止运动，设点Q的运动时间为t(秒).连结PQ、AC、CP、CQ．
(1)点P到点C时，t=______；当点Q到终点时，PC的长度为______；
(2)用含t的代数式表示PD的长；
(3)当三角形CPQ的面积为9时，求t的值．


答案和解析

1.【答案】D 
【解析】解：A、原图不是中心对称图形，是轴对称图形，故此选项不合题意；
B、原图是中心对称图形，不是轴对称图形，故此选项不合题意；
C、原图不是中心对称图形，是轴对称图形，故此选项不合题意；
D、原图既是中心对称图形，又是轴对称图形，故此选项符合题意；
故选：D．
根据中心对称图形与轴对称图形的概念进行判断即可．
本题考查的是中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后与自身重合．

2.【答案】D 
【解析】解：A.该方程是一元一次方程，故本选项不符合题意；
B.该方程是分式方程，故本选项不符合题意；
C.该方程中含有两个未知数，不是一元二次方程，故本选项不符合题意；
D.该方程是一元二次方程，故本选项符合题意．
故选：D．
只含有一个未知数，且未知数的最高次数是2的整式方程叫做一元二次方程．一元二次方程有三个特点：(1)只含有一个未知数；(2)未知数的最高次数是2；(3)是整式方程．
此题主要考查了一元二次方程的定义，要判断一个方程是否为一元二次方程，先看它是否为整式方程，若是，再对它进行整理．如果能整理为ax2+bx+c=0(a≠0)的形式，则这个方程就为一元二次方程．

3.【答案】A 
【解析】解：∵S甲2=1.5cm2，S乙2=2.5cm2，
∴S甲2 ∴甲班选手的身高比乙班选手的整齐．
故选：A．
根据方差的意义可作出判断．
本题考查方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．

4.【答案】A 
【解析】解：根据反证法就是从结论的反面出发进行假设，
∴证明“一个三角形中至多有一个钝角”，应假设：一个三角形中至少有两个钝角．
故选：A．
根据反证法就是从结论的反面出发进行假设，直接假设出一个三角形中至少有两个钝角即可．
此题主要考查了反证法的第一步，根据题意得出命题结论的反例是解决问题的关键．

5.【答案】B 
【解析】解：由题意可得，
100(1−x)2=81，
故选：B．
根据药品经过两次降价，每瓶零售价由100元降为81元，可以列出方程100(1−x)2=81，本题得以解决．
本题考查由实际问题抽象出一元二次方程，解答本题的关键是明确题意，列出相应的方程．

6.【答案】B 
【解析】解：根据题意，得a=2，b=−3．
∴a+b=−1.故选B．
平面直角坐标系中任意一点P(x,y)，关于原点的对称点是(−x,−y).根据这一结论求得a，b的值，再进一步计算．
关于原点对称的点坐标的关系，是需要识记的基本问题，记忆方法是结合平面直角坐标系的图形记忆．

7.【答案】B 
【解析】解：由题意得：Δ=b2−4ac=(−4 2)2−8k=32−8k，
∵原方程两个不相等的实数根，
∴Δ=32−8k>0，
解得：k<4，
∵k≠0，
∴k<4且k≠0．
故选：B．
根据一元二次方程中：Δ=b2−4ac>0，方程有两个不相等的实数根，Δ=b2−4ac=0，方程有两个相等的实数根，Δ=b2−4ac<0，方程没有实数根；从而得到关于k的不等式，解不等式，同时k≠0，即可求解．
本题考查了一元二次方程根的判别式与方程根的个数之间的关系，掌握此关系是解题的关键．

8.【答案】D 
【解析】解：∵四边形ABCD的对角线AC，BD相交于点O，且OA=OC，OB=OD，
∴四边形ABCD为平行四边形，
∴AB/​/CD，∠BAD=∠DCB，AD=BC．
所以A、B、C三项均成立，
故选：D．
根据性质可以推出此四边形ABCD为平行四边形，然后根据平行四边形的性质即可判断．
本题主要考查平行四边形的判定和性质，关键在于根据：若四边形的对角线互相平分，则此四边形为平行四边形这一判定定理判定四边形ABCD为平行四边形．

9.【答案】B 
【解析】解：∵四边形ABCD是平行四边形，
∴AO=OC=5，BO=DO，
∵△AOB的周长是11，
∴AB+BO+AO=11，
∴BO=11−5−4=2，
∴BD=4，
故选：B．
由平行四边形的性质可得AO=OC=5，BO=DO，即可求解．
本题考查了平行四边形的性质，掌握平行四边形的对角线互相平分是解题的关键．

10.【答案】C 
【解析】解：∵四边形ABCD为平行四边形，
∴AB=CD
∵BD=CD，
∴BD=BA，
又∵AM⊥BD，DN⊥AB，
∴S△ABD=12AB⋅DN=12BD⋅AM，
∴DN=AM=6，
∵∠ABD=∠MAP+∠PAB，∠ABD=∠P+∠BAP，
∴∠P=∠PAM，
∴AM=MP=6，
∵∠AMP=90°，
∴AP= AM2+MP2=6 2．
故选：C．
根据BD=CD，AB=CD，可得BD=BA，再根据AM⊥BD，DN⊥AB，即可得到DN=AM=6，依据∠ABD=∠MAP+∠PAB，∠ABD=∠P+∠BAP，即可得到∠P=∠PAM，求出AM=MP=6，最后根据勾股定理求出AP的值即可．
本题主要考查了等腰三角形的判定，平行四边形的性质，三角形面积的计算，勾股定理，求出AM=MP=6是解题的关键．

11.【答案】x≥2 
【解析】解：根据题意，
∵二次根式 3x−6有意义，
∴3x−6≥0，
∴x≥2．
故答案为：x≥2．
根据被开方数大于或等于0，即可求出答案．
本题考查了二次根式有意义的条件，解题的关键是掌握被开方数大于或等于0．

12.【答案】4 
【解析】解：依题意，当x=1时，原方程为1+3−k=0，
解得k=4．
故答案为：4．
根据题意，将x=1代入原方程中，可求k的值．
本题考查了一元二次方程解的定义，掌握方程的解是使方程左右两边成立的未知数的值是解题关键．

13.【答案】x1=−2，x2=2 
【解析】解：x2−4=0，
x2=4，
∴x=±2，
∴x1=−2，x2=2，
故答案为：x1=−2，x2=2．
利用直接开平方法求解即可．
本题考查了一元二次方程的解法−直接开平方法，利用直接开平方法求解一元二次方程的一般步骤：①把方程化为左平方，右常数；②把系数化为1；③开平方取正负；④分开求得方程解．

14.【答案】120° 
【解析】解：六边形的内角和为：(6−2)×180°=720°，
每个内角的度数为：720°÷6=120°，
故答案为：120°．
根据多边形的内角和公式求出六边形的内角和，计算出每个内角的度数即可．
本题考查的是多边形的内角和外角的计算，掌握多边形的内角和公式：(n−2)⋅180°是解题的关键．

15.【答案】60 
【解析】解：∵四边形ABCD是平行四边形，
∴AD/​/BC，∠A=∠C，
∴∠A+∠B=180°，
∵∠A+∠C=240°，
∴∠A=120°，
∴∠B=180°−120°=60°，
故答案为：60．
根据平行四边形的性质可得AD//BC，∠A=∠C，从而可得∠A的度数，再根据AD//BC可得∠A+∠B=180°，进而可得答案．
此题主要考查了平行四边形的性质，关键是掌握平行四边形的对角相等．

16.【答案】5 
【解析】
【分析】
本题考查了中位数、平均数，将数据从小到大依次排列是解题的关键．
【解答】
解：x=5×5−2−3−5−7=8，
这组数据为2，3，5，7，8，
故中位数为5．  
17.【答案】28cm 
【解析】解：在▱ABCD中，BO=OD，
又∵E，F分别是AB，BC的中点，
∴AD=2OE，CD=2OF，
∵OE=4cm，OF=3cm，
∴AD=8cm，CD=6cm，
∴平行四边形ABCD的周长为2(AD+CD)=2(8+6)=28(cm)，
故答案为：28cm．
由平行四边形性质得BO=OD，由三角形中位线性质得AD=2OE，CD=2OF，于是周长为2(AD+CD)=28(cm)．
本题考查平行四边形的性质，三角形中位线的性质，由相关定理得出线段之间的数量关系是解题的关键．

18.【答案】2 
【解析】解：∵四边形ABCD是平行四边形，
∴AB=CD=6，AD//BC，AD=BC=10，
∴∠AEB=∠EBC，
∵BE平分∠ABC，
∴∠ABE=∠CBE，
∴∠ABE=∠AEB，
∴AE=AB=6，
同理DF=CD，
∴AE=DF，
即AE−EF=DF−EF，
∴AF=DE，
∵AB=6，BC=10，
∴DE=AD−AE=10−6=4，
∴EF=DF−DE=6−4=2．
故答案为：2．
证出∠ABE=∠AEB，则AB=AE，同理DF=CD，则AE=DF，进而得出EF的长．
本题考查了平行四边形的性质，平行线的性质，角平分线的性质，等腰三角形的判定等知识；熟练掌握平行四边形的性质，证出AE=DF是解此题的关键．

19.【答案】4 
【解析】解：设AB长为a，AC长为b，
∵在△ABC中，∠BAC=90°，AD为BC边上中线且AD= 5，
∴BC=2 5，
∴a2+b2=(2 5)2=20，
又∵△ABC周长为6+2 5，
∴a+b=6+2 5−2 5=6，
∴ab=12[(a+b)2−(a2+b2)]=12[36−20]=8．
∴△ABC的面积为：12ab=12×8=4．
故答案为：4．
设AB长为a，AC长为b，根据AD为直角三角形ABC斜边BC的中线，可求出BC的长度，即求出a2+b2的值，然后根据△ABC周长为6+2 5，可求出a+b的值，求解即可．
本题考查了二次根式的应用，解答本题的关键在于根据AD为直角三角形ABC斜边BC的中线，求出BC的长度．

20.【答案】(3,4)或(1,−2)或(−1,2) 
【解析】
【分析】
此题考查了平行四边形的性质：平行四边形的对边平行且相等．解题的关键是要注意数形结合思想的应用．
由平行四边形的性质：平行四边形的对边平行且相等，即可求得点C的坐标；注意三种情况．
【解答】
解：如图所示：

∵以O、A、B、C为顶点的四边形是平行四边形，O(0,0)，A(1,3)，B(2,1)，
∴三种情况：
①当AB为对角线时，点C的坐标为(3,4)；
②当OB为对角线时，点C的坐标为(1,−2)；
③当OA为对角线时，点C的坐标为(−1,2)；
故答案为(3,4)或(1,−2)或(−1,2)．  
21.【答案】解：(1)原式=3 2− 2
=2 2；

(2)原式=( 3)2−4
=3−4
=−1． 
【解析】(1)直接化简二次根式，再合并得出答案；
(2)直接利用平方差公式计算，进而合并得出答案．
此题主要考查了二次根式的混合运算，正确化简二次根式是解题关键．

22.【答案】解：(1)x2−2x−2=0，
                  x2−2x=2，
          则x2−2x+1=2+1，
         即(x−1)2=3，
                     x−1=± 3，
∴x1=1+ 3，x2=1− 3；

(2)         (x+1)(x+2)=2x+4，
 (x+1)(x+2)−2(x+2)=0，
                  (x+2)(x−1)=0，
                        x+2=0或x−1=0，
                         ∴x1=−2，x2=1． 
【解析】(1)将常数项移到方程的右边，两边都加上一次项系数一半的平方配成完全平方式后，再开方即可得；
(2)先移项，再将左边利用提公因式法因式分解，继而可得两个关于x的一元一次方程，分别求解即可得出答案．
本题主要考查解一元二次方程的能力，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．

23.【答案】证明：∵∠D=∠DCE，
∴AD/​/BC，
∵AD=BC，
∴四边形ABCD是平行四边形． 
【解析】先证AD//BC，再由四边形一组对边平行且相等的四边形是平行四边形即可得证．
此题考查了平行四边形的判定、平行线的判定，熟练掌握平行四边形的判定定理是解题的关键．

24.【答案】解：(1)如图1所示；

(2)如图2所示；
(3)如图3所示． 
【解析】(1)根据轴对称定义，在最上一行中间一列涂上阴影即可；
(2)根据中心对称定义，在最下一行、最右一列涂上阴影即可；
(3)在最上一行、中间一列，中间一行、最右一列涂上阴影即可．
本题主要考查轴对称图形和中心对称图形，掌握轴对称图形和中心对称图形定义是解题的关键．

25.【答案】证明：∵四边形ABCD是平行四边形，
∴AB=CD，AB/​/CD，
∴∠ABE=∠CDF，
∵AE⊥BD，CF⊥BD，
∴∠AEB=∠CFD=90°，
在△ABE和△CDF中，
∠AEB=∠CFD∠ABE=∠CDFAB=CD，
∴△ABE≌△CDF(AAS)，
∴BE=DF，
∵OB=OD，
∴OB−BE=OD−DF，
∴OE=OF． 
【解析】根据平行四边形的性质得出AB=CD，AB/​/CD，根据平行线的性质得出∠ABE=∠CDF，求出∠AEB=∠CFD=90°，根据AAS推出△ABE≌△CDF，得出对应边相等即可．
本题考查了平行四边形的性质，平行线的性质，全等三角形的判定和性质的应用；证明三角形全等是解决问题的关键．

26.【答案】(1)180
(2)(x−8)
(3)(400−20x) 
【解析】解：(1)当x=11时，销售量为200−20×(11−10)=180(双)．
故答案为：180．
(2)设销售单价为x元，则每双的盈利为(x−8)元，每天的销售量为200−20(x−10)=(400−20x)双．
故答案为：(x−8)；(400−20x)．
(3)依题意得：(x−8)(400−20x)=640，
整理得：x2−28x+192=0，
解得：x1=12，x2=16．
又∵要使顾客得到实惠，
∴x=12．
答：销售单价应该定为12元．
(1)利用销售量=200−20×上涨的价格，即可求出当x=11时每天的销售量；
(2)设销售单价为x元，则每双的盈利为(x−8)元，利用利用销售量=200−20×上涨的价格，即可用含x的代数式表示出每天的销售量；
(3)根据该商店每天销售公筷的盈利=每双的盈利×每天的销售量，即可得出关于x的一元二次方程，解之即可得出x的值，再结合又要使顾客得到实惠，即可确定x的值．
本题考查了一元二次方程的应用以及列代数式，解题的关键是：(1)根据各数量之间的关系，列式计算；(2)根据各数量之间的关系，用含x的代数式表示出每双的盈利及每天的销售量；(3)找准等量关系，正确列出一元二次方程．

27.【答案】解：(1)6s，4； 
(2)  当0≤t≤2时，PD=4−2t；
  当2    当6≤t≤8时，PD=8−(2t−12)=20−2t；
(3)当0≤t≤2时，AP=2t  ，  PD=4−2t  ，  AQ=t  ，  BQ=8−t，
S△CPQ=4×8−12t·2t−12(8−t)·4−12(4−2t )·8=−t2+10t=9，
解得t1=1，t2=9(舍去)；
当2 S△CPQ=12(12−2t)×4=24−4t=9，
解得：t=154；
当6≤t≤8时，PC=2t−12，
S△CPQ=12(2t−12)×4=4t−24=9，
解得：t=334(不合题意，舍去)．
综上所述，当三角形CPQ的面积为9时t=1或t=154． 
【解析】
【分析】
本题考查了矩形的性质和一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．
(1)点P到点C时，所走路程为AD+CD，除以速度求出t的值，当点Q到终点时，P点回到CD中点，即可求出PC；
(2)分点P在A→D上时，D→C时，C→D时进行讨论；
(3)同第2问三种情况进行讨论．
【解答】
解：(1)在矩形ABCD中，AB=8，AD=4，
∴CD=AB=8，点P到点C时，所走路程为AD+CD=12，
∴t=122=6s，
当点Q到终点时，t=8s，P点回到CD中点，
∴CP=4．
故答案为6s，4；
(2)见答案；
(3)见答案．