2022-2023学年浙江省绍兴市嵊州市剡城中学教育集团八年级（下）期中数学试卷（含解析）

2022-2023学年浙江省绍兴市嵊州市剡城中学教育集团八年级（下）期中数学试卷

一、选择题（本大题共10小题，共20.0分。在每小题列出的选项中，选出符合题目的一项）

1.  下列标志中，可以看作是中心对称图形的是(    )

A.  B.  C.  D.

2.  一个边形从一个顶点可引条对角线，则为(    )

A.  B.  C.  D.

3.  若，则实数在数轴上的对应点一定在(    )

A. 原点左侧 B. 原点右侧 C. 原点或原点左侧 D. 原点或原点右侧

4.  为考察甲、乙、丙、丁四种小麦的长势，在同一时期分别从中随机抽取部分麦苗，获得苗高单位：的平均数与方差为：，：，则麦苗又高又整齐的是(    )

A. 甲 B. 乙 C. 丙 D. 丁

5.  电影长津湖讲述了一段波澜壮阔的历史，自上映以来，全国票房连创佳绩．据不完全统计，某市第一天票房收入约亿元，第三天票房收入约达到亿元，设票房收入每天平均增长率为，下面所列方程正确的是(    )

A.  B.
C.  D.

6.  三角形两边长分别为和，第三边是方程的解，则这个三角形的周长是(    )

A.  B. 或 C.  D.

7.  关于的一元二次方程有两个实数根，则实数的取值范围是(    )

A.  B. 且 C.  D. 且

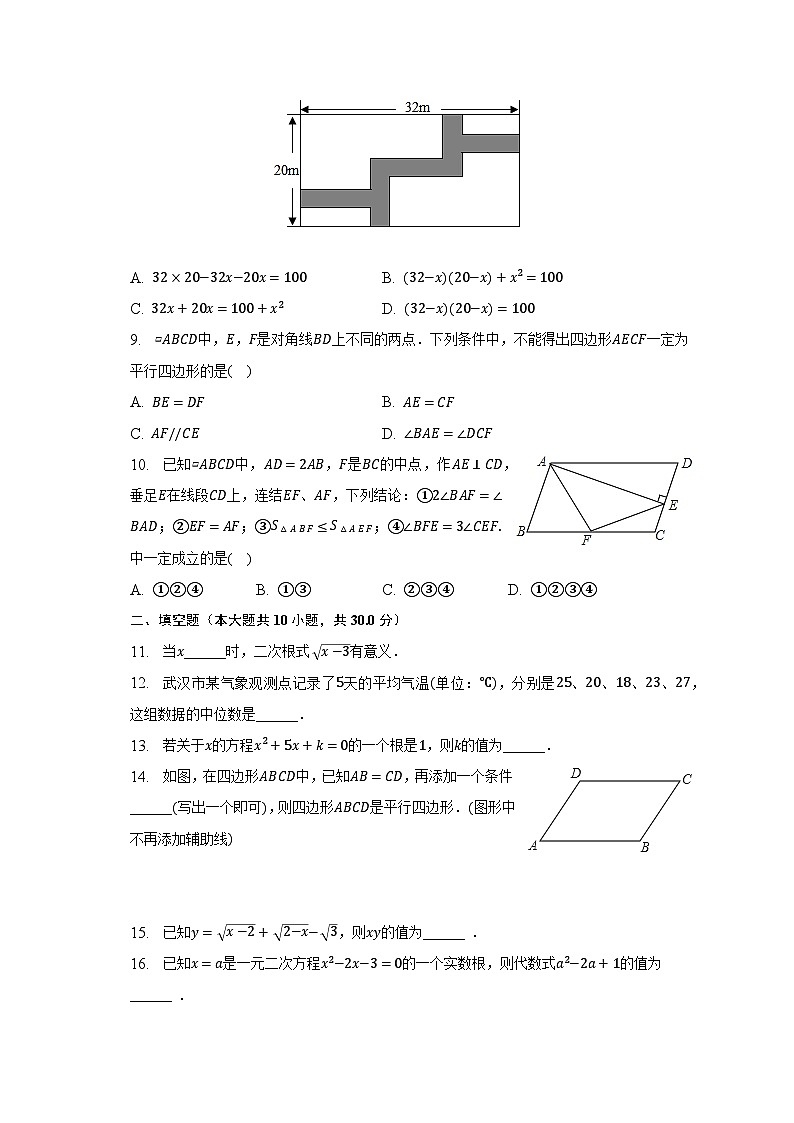
8.  如图，在长为米、宽为米的矩形地面上修筑同样宽的道路图中阴影部分，余下部分种植草坪，要使小路的面积为平方米，设道路的宽为米，则可列方程为(    )

A.  B.
C.  D.

9.  ▱中，，是对角线上不同的两点．下列条件中，不能得出四边形一定为平行四边形的是(    )

A.  B.
C.  D.

10.  已知▱中，，是的中点，作，垂足在线段上，连结、，下列结论：；；；中一定成立的是(    )

A.  B.  C.  D.

二、填空题（本大题共10小题，共30.0分）

11.  当______时，二次根式有意义．

12.  武汉市某气象观测点记录了天的平均气温单位：，分别是、、、、，这组数据的中位数是______．

13.  若关于的方程的一个根是，则的值为______．

14.  如图，在四边形中，已知，再添加一个条件______写出一个即可，则四边形是平行四边形．图形中不再添加辅助线

15.  已知，则的值为______ ．

16.  已知是一元二次方程的一个实数根，则代数式的值为______ ．

17.  若直角三角形的两直角边的长分别为、，且满足，则该直角三角形的斜边长为______．

18.  某中学组织初三学生篮球比赛，以班为单位，每两班之间都比赛一场，计划安排场比赛，则共有______ 个班参赛．

19.  若的整数部分为，小数部分为，则的值为______．

20.  在▱中，对角线与相交于点，在上有一点，连接，过点作的垂线和的延长线交于点，连接，，若，，则______．

三、解答题（本大题共6小题，共50.0分。解答应写出文字说明，证明过程或演算步骤）

21.  本小题分
计算：
；
．

22.  本小题分
解一元二次方程：
；
．

23.  本小题分
年月、日国家实施义务教育质量监测监测部门从某校八年级全体学生中任意抽取名学生，平均分成甲、乙两个小组参加艺术测试根据测试成绩绘制出如下的统计表和统计图．
甲组成绩统计表

请根据上面的信息，解答下列问题：
______ ，甲组成绩的众数是______ ；乙组成绩的中位数是______ ．
请你计算出甲组的平均成绩．
已知甲组成绩的方差，乙组的平均成绩是，请计算出乙组成绩的方差，并判断哪个小组的成绩更均衡？

24.  本小题分
超市销售某种商品，平均每天可售出件，每件盈利元，为了扩大销售，增加盈利该店采取了降价措施，在让顾客得到更大实惠的前提下，经过一段时间销售，发现销售单价每降低元，平均每天可多售出件．
若降价元，则平均每天销售数量为多少件；
当每件商品降价多少元时，该商店每天销售利润为元？

25.  本小题分
如图，在长方形中，，、、、分别从、、、出发沿、、、方向在长方形的边上同时运动，当有一个点先到达所在运动边的另一个端点时即停止，已知在相同时间内，若，则，，．
当为何值时，点的运动停止？
点与点可能相遇吗？点与点呢？请通过计算说明理由．
当为何值时，以、、、为顶点的四边形是平行四边形？

26.  本小题分
我们定义：只有一组对角相等的凸四边形叫做等对角四边形．
四边形是等对角四边形，，若，，则______，______．
图、图均为的正方形网格，线段、的端点均在格点上，按要求以、为边在图、图中各画一个等对角四边形要求：四边形的顶点在格点上，且两个四边形不全等．
如图，在平行四边形中，，，，点为的中点，过点作，交于点点是射线上一个动点，设，求以点、、、为顶点的四边形为等对角四边形时的值．

答案和解析

1.【答案】 

【解析】解：、不是中心对称图形，故本选项错误；
B、不是中心对称图形，故本选项错误；
C、不是中心对称图形，故本选项错误；
D、是中心对称图形，故本选项正确；
故选：．
根据中心对称图形的定义，结合选项所给图形进行判断即可．
本题考查了中心对称图形的知识，判断中心对称图形是要寻找对称中心，图形旋转度后与原图形重合．
 

2.【答案】 

【解析】解：设多边形有条边，
则，
解得．
故选：．
可根据边形从一个顶点引出的对角线与边的关系：，列方程求解．
本题考查了多边形的对角线．解题的关键是明确多边形有条边，则经过多边形的一个顶点所有的对角线有条，经过多边形的一个顶点的所有对角线把多边形分成个三角形．
 

3.【答案】 

【解析】解：，
，
，
实数在数轴上的对应点一定在原点或原点左侧．
故选：．
利用二次根式的性质得出的取值范围，进而结合数轴的特点得出答案．
此题主要考查了二次根式的性质与化简、实数与数轴，正确得出的取值范围是解题关键．
 

4.【答案】 

【解析】解：，
乙、丁的麦苗比甲、丙要高，
，
甲、丁麦苗的长势比乙、丙的长势整齐，
综上，麦苗又高又整齐的是丁，
故选：．
方差越大，表明这组数据偏离平均数越大，数据越不稳定；方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，数据越稳定，据此判断出小麦长势比较整齐的是哪种小麦即可．
此题主要考查了方差的意义和应用，要熟练掌握，解答此题的关键是要明确：方差越大，表明这组数据偏离平均数越大，数据越不稳定；方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，数据越稳定．
 

5.【答案】 

【解析】解：设平均每天票房的增长率为，
根据题意得：．
故选：．
第一天为亿元，根据增长率为得出第二天为亿元，第三天为亿元，根据“第三天票房收入约达到亿元”，即可得出关于的一元二次方程．
本题考查了由实际问题抽象出一元二次方程，找准等量关系，正确列出一元二次方程是解题的关键．
 

6.【答案】 

【解析】解：由，
解得：或，
当第三边长为时，
由三角形三边关系可知：，
故不能组成三角形，
当第三边为时，
由三角形三边关系可知：，能够组成三角形，
这个三角形的周长为：，
故选：．
根据一元二次方程的解法即可求出第三边，然后根据三角形的三边关系即可求出周长．
本题考查一元二次方程的解法，解题的关键是求出利用三角形三边关系求出第三边长．
 

7.【答案】 

【解析】解：关于的一元二次方程有两个实数根，
，
解得，
又，
且，
故选：．
根据关于的一元二次方程有两个实数根知，据此得出的范围，再结合一元二次方程的定义可得答案．
本题主要考查一元二次方程的定义及根的判别式，一元二次方程的根与有如下关系：
当时，方程有两个不相等的实数根；
当时，方程有两个相等的实数根；
当时，方程无实数根．
 

8.【答案】 

【解析】解：设道路的宽米，则
．
故选C．
设道路的宽米，小路的面积一个长宽的矩形面积一个长宽的矩形的面积，即可得出关于的一元二次方程，此题得解．
本题考查了由实际问题抽象出一元二次方程．
 

9.【答案】 

【解析】

【分析】
本题考查了平行四边形的判定与性质，熟练掌握平行四边形的判定方法是解题的关键．
连接与相交于，根据平行四边形的对角线互相平分可得，，再根据对角线互相平分的四边形是平行四边形，只要证明得到即可，然后根据各选项的条件分析判断即可得解．
【解答】
解：如图，连接与相交于，

在▱中，，，
A.若，则，即，所以四边形是平行四边形，故本选项不符合题意；

B.若，则无法证明四边形是平行四边形，故本选项符合题意；
C.，则，
又，
在和中，

≌，
，
四边形是平行四边形，故本选项不符合题意；
D.在▱中，，，
，
，
在和中，

≌，
，然后同可得四边形是平行四边形，故本选项不符合题意．

10.【答案】 

【解析】解：是的中点，
，
在▱中，，
，，
，
，
，
，
，故正确；
延长，交延长线于，
四边形是平行四边形，
，
，
为中点，
，
在和中，
，
≌，
，，
，
，
，
，
，故正确；
，
，
，故正确；
设，则，
，
，
，
，
，故正确，
故选：．
利用平行四边形的性质：平行四边形的对边相等且平行，再由全等三角形的判定得出≌，利用全等三角形的性质得出对应线段之间关系进而得出答案．
此题主要考查了平行四边形的性质以及全等三角形的判定与性质等知识，解决本题的关键是得出≌．
 

11.【答案】 

【解析】解：二次根式有意义，
则，
解得：．
故答案为：．
直接利用二次根式有意义的条件分析得出答案．
此题主要考查了二次根式的有意义的条件，正确把握二次根式的定义是解题关键．
 

12.【答案】 

【解析】解：将数据重新排列为、、、、，
所以这组数据的中位数为，
故答案为：．
根据中位数的概念求解可得．
此题考查了中位数，将一组数据按照从小到大或从大到小的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数．如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数．
 

13.【答案】 

【解析】解：把代入方程得，
解得．
故答案为．
把代入方程得，然后解关于的方程即可．
本题考查了一元二次方程的解：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．
 

14.【答案】 

【解析】解：根据平行四边形的判定，可再添加一个条件：
故答案为：答案不唯一．
可再添加一个条件，根据两组对边分别相等的四边形是平行四边形，四边形是平行四边形．
此题主要考查平行四边形的判定．是一个开放条件的题目，熟练掌握判定定理是解题的关键．
 

15.【答案】 

【解析】解：，
，，
，
，
，
，
故答案为：．
直接利用二次根式有意义的条件得出的值，进而得出的值进而得出答案．
此题主要考查了二次根式有意义的条件，正确得出，的值是解题关键．
 

16.【答案】 

【解析】解：是一元二次方程的一个实数根，
，
，

故答案为：．
根据方程的解的定义把代入一元二次方程，得到，然后将其整体代入所求的代数式进行求值．
本题考查了一元二次方程的解的定义，解题的关键是整体代入思想的应用．
 

17.【答案】 

【解析】解：，
，，
该直角三角形的斜边长为：．
故答案为：．
直接利用偶次方的性质以及二次根式的性质得出，的值，再利用勾股定理得出斜边长．
此题主要考查了勾股定理以及偶次方的性质和二次根式的性质，正确得出，的值是解题关键．
 

18.【答案】 

【解析】解：设共有个班参赛，
根据题意得：，
解得：，不合题意，舍去．
故答案为：．
设共有个班参赛，根据每两班之间都比赛一场且计划安排场比赛，即可得出关于的一元二次方程，解之取其正值即可得出结论．
本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．
 

19.【答案】 

【解析】

【分析】
此题主要考查了估算无理数的大小，正确得出的取值范围是解题关键．
估算的取值范围从而得出，的值，进而得出答案．
【解答】
解：，
，
的整数部分，小数部分为，
故

．
故答案为．  

20.【答案】 

【解析】解：延长、交于点，

四边形是平行四边形，
，
，
，
，
，
，
在和中，
，
≌，
，，
中，，
，
，
，
中，，
故答案为：．
作辅助线，构建全等三角形和直角三角形，证明≌，得，，计算的长，在中，根据勾股定理可得的长．
本题考查平行四边形的性质、全等三角形的判定和性质、勾股定理，解题的关键是灵活运用所学知识解决问题，学会添加常用辅助线，构造直角三角形解决问题，属于中考常考题型．
 

21.【答案】解：原式
；
原式
． 

【解析】原式根据平方差公式进行计算即可；
先根据完全平方公式去括号，再进行二次根式的乘法运算，最后进行加减运算即可．
本题主要考查了二次根式的混合运算，熟练掌握运算法则和乘法公式是解答本题的关键．
 

22.【答案】解：，
，
或，
解得，；
解：，
，，，
，
，
，． 

【解析】利用因式分解法求解；
利用公式法求解．
本题考查解一元二次方程，掌握因式分解法、公式法是解题的关键．
 

23.【答案】     

【解析】解：；由统计表可知：甲组成绩的众数是；乙组的中位数是第，位数的平均数，由图可知是．
故答案为：，，；
甲组平均成绩为：；




，
，
，
乙更均衡．
根据统计表、中位数和众数的定义即可确定；
根据平均数的计算方法运算即可；
计算出乙组的方差，再比较甲、乙两组的方差大小即可．
本题考查统计表与条形统计图、方差、中位数、众数、平均数的相关内容，注意从图中获取信息，分析图中数据之间的数量关系，掌握常见统计运算方法是解题的关键．
 

24.【答案】解：根据题意得：件，
答：平均每天销售数量为件；
设每件商品降价元，则每件盈利元，平均每天可售出元，依题意得：
，
整理得：，
解得：，，
又要让顾客得到更大实惠，
．
答：当每件商品降价元时，该商店每天销售利润为元． 

【解析】利用平均每天的销售量每件商品降低的价格，即可求出结论；
设每件商品降价元，则每件盈利元，平均每天可售出元，利用总利润每件盈利平均每天的销售量，即可得出关于的一元二次方程，解之即可得出的值，再结合在让顾客得到更大实惠的前提下，即可得出每件商品应降价元．
本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．
 

25.【答案】解：由题意得，
，
当为时，点的运动停止；
当点与点相遇时，，
解得或舍去，
当点与点相遇时，，
解得，
当时，，
点与点不能相遇；
当点到达点时，，
，
，，
，
此时点与点还未相遇，
点只能在点的左侧，
如图，当点在点的左侧时，

，
解得舍去或，
当时，以、、、为顶点的四边形是平行四边形；
如图，当点在点的右侧时，

，
解得或舍去，
当时，以、、、为顶点的四边形是平行四边形，
综上，当或时，以、、、为顶点的四边形是平行四边形． 

【解析】根据题意知，当点运动到终点时，运动停止；
当点与点相遇时，，解得或舍去，当点与点相遇时，，解得，故舍去；
首先计算可得点只能在点的左侧，然后分当点在点的左侧或点在点的右侧两种情形，分别根据，列方程可解决问题．
本题主要考查了矩形的性质，平行四边形的性质，化动为静，运用分类讨论思想是解题的关键．
 

26.【答案】   

【解析】解：四边形是“等对角四边形”，，
，
；
故答案为：，；

等对角四边形如图所示：


如图，作于，

中，，
，
，
．
点为的中点，
，
．
如图，当时，，
，
．
如图，连接．
，，
为等边三角形．
当时，则，
．
综上所述，或．
由等对角四边形得出，再由四边形内角和即可求出；
如图，由等对角四边形的定义作出，如图，由等对角四边形的定义作出；
过点作于点，则四边形为矩形，根据三角函数求出和，分两种情况进行讨论：当时；当时，即可得出答案．
本题属于四边形综合题目，主要考查了四边形内角和定理、等腰三角形的判定与性质、勾股定理、直角三角形的性质、矩形的判定与性质等知识；熟练掌握直角三角形的性质是解题的关键．