2022-2023学年庐江县数学七下期末达标测试试题含答案

2022-2023学年庐江县数学七下期末达标测试试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

考生请注意：

1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。

2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。

3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。

一、选择题(每小题3分,共30分)

1．正方形的一条对角线之长为3，则此正方形的边长是（     ）

A． B．3 C． D．

2．若直线经过第一、二、四象限，则化简的结果是 (      )

A．2  k B．2  k C．k  2 D．不能确定

3．下列变形是因式分解的是（　　）

A．x（x+1）＝x2+x B．m2n+2n＝n（m+2）

C．x2+x+1＝x（x+1）+1 D．x2+2x﹣3＝（x﹣1）（x+3）

4．甲、乙两人加工同一种服装，乙每天比甲多加工1件，乙加工服装24件所用时间与甲加工服装20件所用时间相同。设甲每天加工服装x件。由题意可得方程（    ）

A． B．

C． D．

5．如图，▱ABCD中，对角线AC，BD相交于点O，OA＝3，若要使平行四边形ABCD为矩形，则OB的长度为（　　）

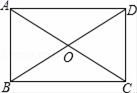
A．4 B．3 C．2 D．1

6．在中，AB=15,AC=20,BC边上高AD=12,则BC的长为(    )

A．25 B．7 C．25或7  D．不能确定

7．勾股定理是“人类最伟大的十个科学发现之一”.中国对勾股定理的证明最早出现在对《周髀算经》的注解中，它表现了我国古人对数学的钻研精神和聪明才智，是我国古代数学的骄傲.在《周髀算经》注解中证明勾股定理的是我国古代数学家（   ）

A．祖冲之 B．杨辉 C．刘徽 D．赵爽

8．下列二次根式是最简二次根式的是（　　）

A． B． C． D．

9．关于圆的性质有以下四个判断：①垂直于弦的直径平分弦，②平分弦的直径垂直于弦，③在同圆或等圆中，相等的弦所对的圆周角相等，④在同圆或等圆中，相等的圆周角所对的弦相等，则四个判断中正确的是（　　）

A．①③ B．②③ C．①④ D．②④

10．如图，正方形ABCD的边长为8，点M在DC上，且DM=2，N是AC上一动点，则DN+MN的最小值为（）

A．8 B． C． D．10

二、填空题(本大题共有6小题，每小题3分，共18分)

11．《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架，书中的算法体系至今仍在推动着计算机的发展和应用.《九章算术》中记载：今有户不知高、广，竿不知长、短.横之不出四尺，从之不出二尺，邪之适出.问户高、广、邪各几何?译文是：今有门不知其高、宽，有竿，不知其长、短，横放，竿比门宽长出尺；竖放，竿比门高长出尺；斜放，竿与门对角线恰好相等.问门高、宽、对角线长分别是多少?若设门对角线长为尺，则可列方程为__________．

12．如图显示了小亚用计算机模拟随机投掷一枚某品牌啤酒瓶盖的实验结果.

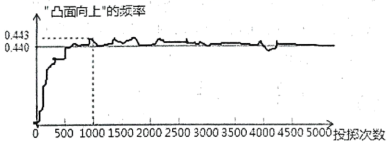
那么可以推断出如果小亚实际投掷一枚品牌啤酒瓶盖时，“凸面向上”的可能性 _________“凹面向上”的可能性.（填“大于”，“等于”或“小于”）.

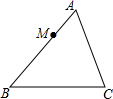
13．如图，在△ABC中，AB=9，AC=6，BC=12，点M在AB边上，且AM=3，过点M作直线MN与AC边交于点N，使截得的三角形与原三角形相似，则MN=______．

14．若是的小数部分，则的值是______．

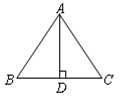
15．如图，等腰三角形中，，是底边上的高，则AD=________________.

16．在平面直角坐标系中，点关于轴对称的点的坐标是__________．

三、解下列各题(本大题共8小题，共72分)

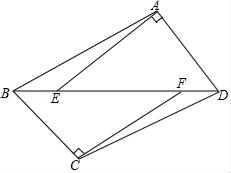
17．（8分）已知：如图，在四边形ABCD中，过A，C分别作AD和BC的垂线，交对角线BD于点E，F，AE＝CF，BE＝DF．

（1）求证：四边形ABCD是平行四边形；

（2）若BC＝4，∠CBD＝45°，且E，F是BD的三等分点，求四边形ABCD的面积．（直接写出结论即可）

18．（8分）因魔幻等与众不同的城市特质，以及抖音等新媒体的传播，重庆已成为国内外游客最喜欢的旅游目的地城市之一．著名“网红打卡地”磁器口在2018年五一长假期间，接待游客达20万人次，预计在2020年五一长假期间，接待游客将达28.8万人次．在磁器口老街，美食无数，一家特色小面店希望在五一长假期间获得好的收益，经测算知，该小面成本价为每碗6元，借鉴以往经验：若每碗卖25元，平均每天将销售300碗，若价格每降低1元，则平均每天多销售30碗．

(1)求出2018至2020年五一长假期间游客人次的年平均增长率；

(2)为了更好地维护重庆城市形象，店家规定每碗售价不得超过20元，则当每碗售价定为多少元时，店家才能实现每天利润6300元？

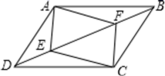
19．（8分）如图，在平行四边形ABCD中，E，F为对角线BD上的两点，且∠DAE＝∠BCF．

求证：（1）AE＝CF；

（2）四边形AECF是平行四边形．

20．（8分）已知一次函数的图象经过点（-2，-7）和（2，5），求该一次函数解析式并求出函数图象与y轴的交点坐标.

21．（8分）解答题．

某校学生积极为地震灾区捐款奉献爱心．小颖随机抽查其中30名学生的捐款情况如下：（单位：元）2、5、35、8、5、10、15、20、15、5、45、10、2、8、20、30、40、10、15、15、30、15、8、25、25、30、15、8、10、1．

（1）这30名学生捐款的最大值、最小值、极差、平均数各是多少？

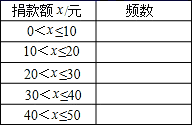
（2）将30名学生捐款额分成下面5组，请你完成频数统计表：

（3）根据上表，作出频数分布直方图．

22．（10分）（1）计算：

（2）解方程：(1－2x)2＝x2－6x＋9

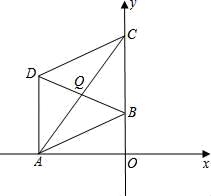
23．（10分）如图，在直角坐标系中，OA＝3，OC＝4，点B是y轴上一动点，以AC为对角线作平行四边形ABCD．

(1)求直线AC的函数解析式；

(2)设点B(0，m)，记平行四边形ABCD的面积为S，请写出S与m的函数关系式，并求当BD取得最小值时，函数S的值；

(3)当点B在y轴上运动，能否使得平行四边形ABCD是菱形？若能，求出点B的坐标；若不能，说明理由．

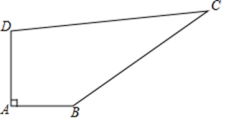
24．（12分）求知中学有一块四边形的空地ABCD，如下图所示，学校计划在空地上种植草皮，经测量∠A=90°，AB=3m，BC=12m，CD=13m，DA=4m，若每平方米草皮需要250元，问学校需要投入多少资金买草皮？

参考答案

一、选择题(每小题3分,共30分)

1、A

2、B

3、D

4、C

5、B

6、C

7、D

8、B

9、C

10、D

二、填空题(本大题共有6小题，每小题3分，共18分)

11、．

12、小于

13、4或1

14、1

15、1

16、

三、解下列各题(本大题共8小题，共72分)

17、（1）证明见解析；（2）1.

18、 (1)年平均增长率为20%；(2)每碗售价定为20元时，每天利润为6300元.

19、（1）详见解析；（2）详见解析

20、y=3x-1, 函数图象与y轴的交点坐标(0,-1).

21、 (1) 最大值为1，最小值为2，极差为48，平均数为17.7元．(2)填表见解析；（3）补图见解析.

22、（1）- （2）-2、

23、（1）；(2)  ①当m≤4时，S=－3m+12，②当m＞4时，S=3m－12（3）（0，）

24、学校需要投入9000元资金买草皮．