


2022-2023学年广东省茂名市电白县七年级数学第二学期期末检测试题含答案
展开2022-2023学年广东省茂名市电白县七年级数学第二学期期末检测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生请注意:
1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.二次根式![]() 在实数范围内有意义, 则x的取值范围是( )
在实数范围内有意义, 则x的取值范围是( )
A.x≥-3 B.x≠3 C.x≥0 D.x≠-3
2.如图,在矩形ABCD中,点E在AD上,且EC平分∠BED,AB=1,∠ABE=45°,则BC的长为( )
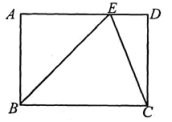
A.![]() B.1.5 C.
B.1.5 C.![]() D.2
D.2
3.如图,延长矩形 ABCD 的边 BC 至点 E ,使 CE BD ,连接 AE ,若 ∠ADB 40 ,则 ∠E 的度数是( )
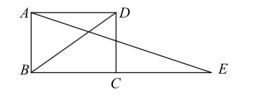
A.20 B.25 C.30 D.35
4.下列各组长度的线段(单位:![]() )中,成比例线段的是( )
)中,成比例线段的是( )
A.1,2,3,4 B.1,2,3,6 C.2,3,4,5 D.1,3,5,10
5.今年,重庆市南岸区广阳镇一果农李灿收获枇杷20吨,桃子12吨,现计划租用甲、乙两种货车共8辆将这批水果全部运往外地销售,已知一辆甲种货车可装枇杷4吨和桃子1吨,一辆乙种货车可装枇杷和桃子各2吨.李灿安排甲、乙两种货车一次性地将水果运到销售地的方案数有( )
A.1种 B.2种 C.3种 D.4种
6.某型号的汽车在路面上的制动距离s=![]() ,其中变量是( )
,其中变量是( )
A. s v2 B.s C.v D. s v
7.每千克m元的糖果x千克与每千克n元的糖果y千克混合成杂拌糖,则这种杂拌糖每千克的价格为 ( )
A.![]() 元 B.
元 B.![]() 元 C.
元 C.![]() 元 D.
元 D.![]() 元
元
8.某种商品的进价为800元,出售时标价为1200元,后来由于该商品积压,商店准备打折销售,但要保证利润率不低于5%,则至多可打( )
A.6折 B.7折
C.8折 D.9折
9.如图,在直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 在
在![]() 上,且
上,且![]() 于
于![]() ,则
,则![]() =( )
=( )
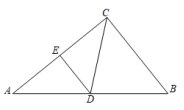
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.把一元二次方程x2﹣6x+1=0配方成(x+m)2=n的形式,正确的是( )
A.(x+3)2=10 B.(x﹣3)2=10 C.(x+3)2=8 D.(x﹣3)2=8
11.使分式![]() 无意义,则x的取值范围是( )
无意义,则x的取值范围是( )
A.x ≠ 1 B.x=1 C.x<1 D.x ≠-1
12.甲、乙、丙、丁四人进行射击测试,每人10次射击成绩的平均数都均为8.8环,方差分别为S甲2=0.63,S乙2=0.51,S丙2=0.48,S丁2=0.42,则四人中成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.画在比例尺为![]() 的图纸上的某个零件的长是
的图纸上的某个零件的长是![]() ,这个零件的实际长是_______
,这个零件的实际长是_______![]() .
.
14.用换元法解方程![]() 时,如果设
时,如果设![]() ,那么得到关于
,那么得到关于![]() 的整式方程为_____.
的整式方程为_____.
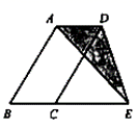
15.如图,在![]() 中,
中,![]() 为边
为边![]() 延长线上一点,且
延长线上一点,且![]() ,连结
,连结![]() 、
、![]() .若
.若![]() 的面积为1,则
的面积为1,则![]() 的面积为____.
的面积为____.
16.化简![]() 的结果等于_____________.
的结果等于_____________.
17.已知一组数据1,5,7,x的众数与中位数相等,则这组数据的平均数是___________.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)一手机经销商计划购进某品牌的A型、B型、C型三款手机共60部,每款手机至少要购进8部,且恰好用完购机款61000元.设购进A型
手机x部,B型手机y部.三款手机的进价和预售价如下表:
手机型号 | A型 | B型 | C型 |
进 价(单位:元/部) | 900 | 1200 | 1100 |
预售价(单位:元/部) | 1200 | 1600 | 1300 |
(1)用含x,y的式子表示购进C型手机的部数;
(2)求出y与x之间的函数关系式;
(3)假设所购进手机全部售出,综合考虑各种因素,该手机经销商在购销这批手机过程中需另外支出各种费用共1500元.
①求出预估利润P(元)与x(部)的函数关系式;
(注:预估利润P=预售总额-购机款-各种费用)
②求出预估利润的最大值,并写出此时购进三款手机各多少部.
19.(5分)如图,在平面直角坐标系中,点A的坐标为(0,6),点B在x轴的正半轴上.若点P、Q在线段AB上,且PQ为某个一边与x轴平行的矩形的对角线,则称这个矩形为点P、Q的“涵矩形”。下图为点P、Q的“涵矩形”的示意图.
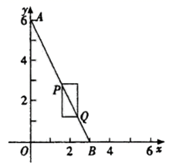
(1)点B的坐标为(3,0);
①若点P的横坐标为![]() ,点Q与点B重合,则点P、Q的“涵矩形”的周长为 .
,点Q与点B重合,则点P、Q的“涵矩形”的周长为 .
②若点P、Q的“涵矩形”的周长为6,点P的坐标为(1,4),则点E(2,1),F(1,2),G(4,0)中,能够成为点P、Q的“涵矩形”的顶点的是 .
(2)四边形PMQN是点P、Q的“涵矩形”,点M在△AOB的内部,且它是正方形;
①当正方形PMQN的周长为8,点P的横坐标为3时,求点Q的坐标.
②当正方形PMQN的对角线长度为/2时,连结OM.直接写出线段OM的取值范围 .
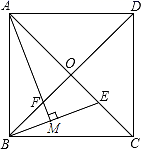
20.(8分)如图,正方形ABCD的边长为2![]() ,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F.
,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F.
(1)求证:AF=BE;
(2)求点E到BC边的距离.
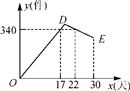
21.(10分)某公司开发出一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为8元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象(如图),图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少5件.
(1)第24天的日销售量是 件,日销售利润是 元;
(2)求y与x之间的函数关系式,并写出x的取值范围;
(3)日销售利润不低于640元的天数共有多少天?试销售期间,日销售最大利润是多少元?
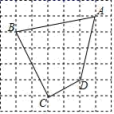
22.(10分)如图,每个小正方形的边长都为1,四边形ABCD的顶点都在小正方形的顶点上.
(1)求四边形ABCD的面积;
(2)∠BCD是直角吗?说明理由.
23.(12分)A、B两地的距离是80千米,一辆巴士从A地驶出3小时后,一辆轿车也从A地出发,它的速度是巴士的3倍,已知轿车比巴士早20分钟到达B地,试求两车的速度。
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、A
2、A
3、A
4、B
5、C
6、D
7、B
8、B
9、C
10、D
11、B
12、D
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、640
14、![]()
15、3
16、![]()
17、4.1
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)60-x-y (2)y=2x-1 (3)①P=10x+10 ②最大值为1710元.
此时购进A型手机3部,B型手机18部,C型手机8部
19、(1)①1,②(1,2);(2)①(1,5)或(5,1),②![]()
20、 (1)见解析;(2)![]() .
.
21、 (1)330;660 (2)答案见解析(3) 日销售利润不低于640元的天数共有11天,试销售期间,日销售最大利润是720元.
22、(1)四边形ABCD的面积=14![]() ;(2)是.理由见解析.
;(2)是.理由见解析.
23、解:设巴士的速度是x千米/小时,轿车的速度是3x千米/小时,
![]()
x=16
经检验x=16是方程的解.
16×3=48
巴士的速度是16千米/小时,轿车的速度是48千米/小时.
广东省茂名市电白县2023-2024学年九年级数学第一学期期末综合测试模拟试题含答案: 这是一份广东省茂名市电白县2023-2024学年九年级数学第一学期期末综合测试模拟试题含答案,共7页。
2023-2024学年广东省茂名市电白县九年级数学第一学期期末质量跟踪监视试题含答案: 这是一份2023-2024学年广东省茂名市电白县九年级数学第一学期期末质量跟踪监视试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,下列方程有实数根的是,二次函数 y=等内容,欢迎下载使用。
广东省茂名市电白县2023-2024学年八上数学期末统考模拟试题含答案: 这是一份广东省茂名市电白县2023-2024学年八上数学期末统考模拟试题含答案,共6页。试卷主要包含了考生要认真填写考场号和座位序号,2-3的倒数是,已知,则的值为,计算,下列说法中正确的个数是,函数y=的自变量x的取值范围是等内容,欢迎下载使用。












