

2022-2023学年广东省韶关市名校数学七年级第二学期期末检测模拟试题含答案
展开2022-2023学年广东省韶关市名校数学七年级第二学期期末检测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1.不等式组![]() 中的两个不等式的解集在数轴上表示为( )
中的两个不等式的解集在数轴上表示为( )
A.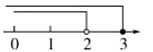 B.
B.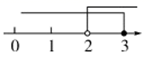
C.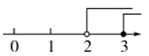 D.
D.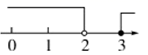
2.若m>n,则下列各式错误的是( )
![]()
A.2m<2n B.-3m<-3n C.m+1>n+1 D.m-5>n-5
3.如图,点A、B、C在一次函数y=3x+m的图象上,它们的横坐标依次为﹣2,﹣1,1,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( )
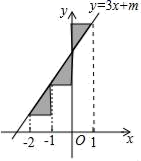
A.![]() B.3 C.3(m+1) D.
B.3 C.3(m+1) D.![]() (m+1)
(m+1)
4.如图,点D是等边△ABC的边AC上一点,以BD为边作等边△BDE,若BC=10,BD=8,则△ADE的周长为( )
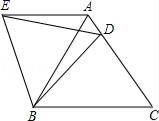
A.14 B.16 C.18 D.20
5.在下列条件中能判定四边形ABCD是平行四边形的是( )
A.AB=BC,AD=DC B.AB//CD,AD=BC
C.AB//CD,∠B=∠D D.∠A=∠B,∠C=∠D
6.甲、乙、丙、丁四名同学在一次投掷实心球训练中,在相同条件下各投掷10次,他们成绩的平均数![]() 与方差s2如下表:
与方差s2如下表:

若要选一名成绩好且发挥稳定的同学参加比赛,则应该选择( )
A.甲 B.乙 C.丙 D.丁
7.在数学活动课上,老师要求同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的四位同学拟定的方案,其中正确的是( )
A.测量对角线是否相互平分 B.测量两组对边是否分别相等
C.测量一组对角是否都为直角 D.测量四边形其中的三个角是否都为直角
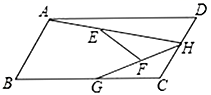
8.如图,已知点E、F分别是△ABC的边AB、AC上的点,且EF∥BC,点D是BC边上的点,AD与EF交于点H,则下列结论中,错误的是( )
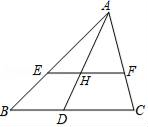
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
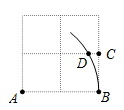
9.如图,在2×2的正方形网格中,每个小正方形边长为1,点A,B,C均为格点,以点A为圆心,AB长为半径作弧,交格线于点D,则CD的长为( )
A.![]() B.
B.![]() C.
C.![]() D.2﹣
D.2﹣![]()
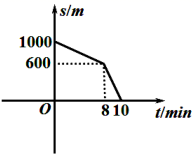
10.放学后,小刚和同学边聊边往家走,突然想起今天是妈妈的生日,赶紧加快速度,跑步回家.小刚离家的距离![]() 和放学后的时间
和放学后的时间![]() 之间的关系如图所示,给出下列结论:①小刚家离学校的距离是
之间的关系如图所示,给出下列结论:①小刚家离学校的距离是![]() ;②小刚跑步阶段的速度为
;②小刚跑步阶段的速度为![]() ;③小刚回到家时已放学10分钟;④小刚从学校回到家的平均速度是
;③小刚回到家时已放学10分钟;④小刚从学校回到家的平均速度是![]() .其中正确的个数是( )
.其中正确的个数是( )
A.4 B.3 C.2 D.1
二、填空题(本大题共有6小题,每小题3分,共18分)
11.已知等腰三角形的两条中位线的长分别为2和3,则此等腰三角形的周长为_____.
12.如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 上的动点.连接
上的动点.连接![]() 、
、![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,连接
的中点,连接![]() .则
.则![]() 的最小值为________.
的最小值为________.
13.一组数据:1,2,1,0,2,a,若它们的众数为1,则这组数据的平均数为_______.
14.直线y=2x+1经过点(a,0),则a=________.
15.解分式方程![]() 时,设
时,设![]() ,则原方程化为关于
,则原方程化为关于![]() 的整式方程是__________.
的整式方程是__________.
16.在菱形ABCD中,∠A=30°,在同一平面内,以对角线BD为底边作顶角为120°的等腰三角形BDE,则∠EBC的度数为 .
三、解下列各题(本大题共8小题,共72分)
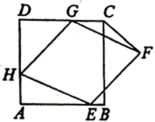
17.(8分)如图,正方形![]() 的边长为6,菱形
的边长为6,菱形![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() 分别在正方形
分别在正方形![]() 的边
的边![]() ,
,![]() ,
,![]() 上,且
上,且![]() ,连接
,连接![]() .
.
(1)当![]() 时,求证:菱形
时,求证:菱形![]() 为正方形;
为正方形;
(2)设![]() ,试用含
,试用含![]() 的代数式表示
的代数式表示![]() 的面积.
的面积.
18.(8分)解方程:![]()
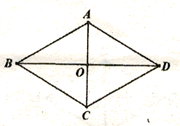
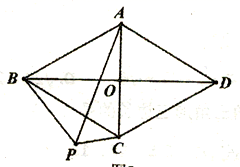
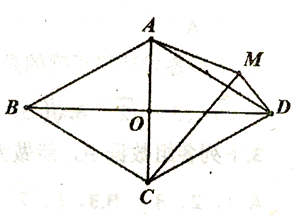
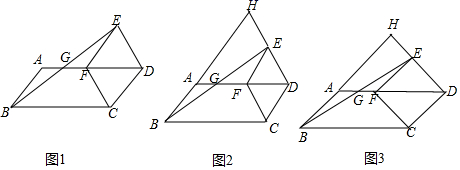
19.(8分)已知在菱形ABCD中,对角线AC、BD交于点O,AB=2AO;(1)如图1,求∠BAC的度数;(2)如图2,P为菱形ABCD外一点,连接AP、BP、CP,若∠CPB=120°,求证:CP+BP=AP;(3)如图3,M为菱形ABCD外一点,连接AM、CM、DM,若∠AMD=150°,
CM=2![]() ,DM=2,求四边形ACDM的面积。
,DM=2,求四边形ACDM的面积。
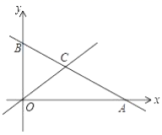
20.(8分)如图,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、点
、点![]() ,与直线
,与直线![]() 交于点
交于点![]() .
.
(1)若![]() ,请直接写出
,请直接写出![]() 的取值范围;
的取值范围;
(2)点![]() 在直线
在直线![]() 上,且
上,且![]() 的面积为3,求点
的面积为3,求点![]() 的坐标?
的坐标?
21.(8分)如图,已知四边形![]() 为正方形,点
为正方形,点![]() 为对角线
为对角线![]() 上的一动点,连接
上的一动点,连接![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,以
,以![]() 为邻边作矩形
为邻边作矩形![]() ,连接
,连接![]() .
.
(1)求证:矩形![]() 是正方形;
是正方形;
(2)判断![]() 与
与![]() 之间的数量关系,并给出证明.
之间的数量关系,并给出证明.
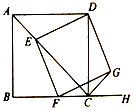
22.(10分)通过类比联想,引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例,先阅读再解决后面的问题:
原题:如图1,点E,F分别在正方形ABCD的边BC,CD上,![]() ,连接EF,求证:EF=BE+DF.
,连接EF,求证:EF=BE+DF.
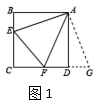
解题分析:由于AB=AD,我们可以延长CD到点G,使DG=BE,易得![]() ,可证
,可证![]() .再证明
.再证明![]() ,得EF=FG=DG+FD=BE+DF.
,得EF=FG=DG+FD=BE+DF.
问题(1):如图2,在四边形ABCD中,AB=AD,![]() ,E,F分别是边BC,CD上的点,且
,E,F分别是边BC,CD上的点,且![]() ,求证:EF=BE+FD;
,求证:EF=BE+FD;
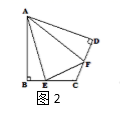
问题(2):如图3,在四边形ABCD中,![]() ,
,![]() ,AB=AD=1,点E,F分别在四边形ABCD的边BC,CD上的点,且
,AB=AD=1,点E,F分别在四边形ABCD的边BC,CD上的点,且![]() ,求此时
,求此时![]() 的周长
的周长
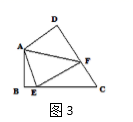
23.(10分)如图1,以□ABCD的较短边CD为一边作菱形CDEF,使点F落在边AD上,连接BE,交AF于点G.
(1)猜想BG与EG的数量关系.并说明理由;
(2)延长DE,BA交于点H,其他条件不变,
①如图2,若∠ADC=60°,求![]() 的值;
的值;
②如图3,若∠ADC=α(0°<α<90°),直接写出![]() 的值.(用含α的三角函数表示)
的值.(用含α的三角函数表示)
24.(12分)某工厂计划生产甲、乙两种产品共2500吨,每生产1吨甲产品可获得利润0.3万元,每生产1吨乙产品可获得利润0.4万元.设该工厂生产了甲产品x(吨),生产甲、乙两种产品获得的总利润为y(万元).
(1)求y与x之间的函数表达式;
(2)若每生产1吨甲产品需要A原料0.25吨,每生产1吨乙产品需要A原料0.5吨.受市场影响,该厂能获得的A原料至多为1000吨,其它原料充足.求出该工厂生产甲、乙两种产品各为多少吨时,能获得最大利润.
参考答案
一、选择题(每小题3分,共30分)
1、C
2、A
3、A
4、C
5、C
6、A
7、D
8、B
9、D
10、A
二、填空题(本大题共有6小题,每小题3分,共18分)
11、14或1
12、![]()
13、![]() .
.
14、![]()
15、![]()
16、105°或45°
三、解下列各题(本大题共8小题,共72分)
17、(1)见解析;(2)![]() .
.
18、x=2
19、(1)∠BAC=60°;(2)见解析;(3)![]() .
.
20、 (1)x>2;(2)(0,3)或(4,1).
21、(1)详见解析;(2)![]() ,理由详见解析.
,理由详见解析.
22、(1)![]() ,见解析;(2)
,见解析;(2)![]() 周长为
周长为![]() .
.
23、(1)![]() ,理由见解析;(2)
,理由见解析;(2)![]() ;(3)
;(3)![]() .
.
24、(1)![]() ;(2)工厂生产甲产品1000吨,乙产品1500吨时,能获得最大利润.
;(2)工厂生产甲产品1000吨,乙产品1500吨时,能获得最大利润.
广东省韶关市名校2023-2024学年八年级数学第一学期期末复习检测模拟试题含答案: 这是一份广东省韶关市名校2023-2024学年八年级数学第一学期期末复习检测模拟试题含答案,共7页。试卷主要包含了答题时请按要求用笔,若,则内应填的式子是,计算的结果是等内容,欢迎下载使用。
广东省韶关市乳源县2022-2023学年数学七年级第二学期期末调研模拟试题含答案: 这是一份广东省韶关市乳源县2022-2023学年数学七年级第二学期期末调研模拟试题含答案,共6页。试卷主要包含了考生要认真填写考场号和座位序号,不能被整除,已知点M的坐标为等内容,欢迎下载使用。
广东省韶关市乐昌县2022-2023学年数学七年级第二学期期末检测模拟试题含答案: 这是一份广东省韶关市乐昌县2022-2023学年数学七年级第二学期期末检测模拟试题含答案,共7页。试卷主要包含了下列各式中的最简二次根式是,如图,点、在函数等内容,欢迎下载使用。












