


2022-2023学年广东省深圳市北大附中深圳南山分校七下数学期末质量检测模拟试题含答案
展开2022-2023学年广东省深圳市北大附中深圳南山分校七下数学期末质量检测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
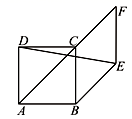
1.如图,四边形ABCD是正方形,AB=1,点F是对角线AC延长线上一点,以BC、CF为邻边作菱形BEFC,连接DE,则DE的长是( ).
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
2.计算![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.有一组数据:3,3,5,6,1.这组数据的众数为( )
A.3 B.5 C.6 D.1
4.已知一次函数y=(k﹣2)x+k+1的图象不过第三象限,则k的取值范围是( )
A.k>2 B.k<2 C.﹣1≤k≤2 D.﹣1≤k<2
5.分式方程![]() 的解是( )
的解是( )
A.3 B.-3 C.![]() D.9
D.9
6.下列函数中,表示y是x的正比例函数的是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
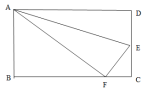
7.如图,矩形![]() 沿
沿![]() 折叠,使
折叠,使![]() 点落在
点落在![]() 边上的
边上的![]() 点处,如果
点处,如果![]() ,那么
,那么![]() 的度数是( )
的度数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
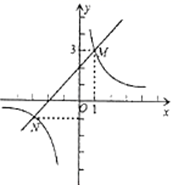
8.如图,双曲线![]() 与直线
与直线![]() 交于点M,N,并且点M坐标为(1,3)点N坐标为(-3,-1),根据图象信息可得关于x的不等式
交于点M,N,并且点M坐标为(1,3)点N坐标为(-3,-1),根据图象信息可得关于x的不等式![]() 的解为( )
的解为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9.通过估算,估计![]() 的大小应在( )
的大小应在( )
A.7~8之间 B.8.0~8.5之间
C.8.5~9.0之间 D.9~10之间
10.下列各式计算正确的是( )
A.(2a2)•(3a3)=6a6 B.6a2b÷2a=3b
C.3a2﹣2a2=a2 D.![]() +
+![]() =
=![]()
二、填空题(本大题共有6小题,每小题3分,共18分)
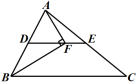
11.如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=10,BC=16,则EF的长为___________.
12.将直线![]() 平移后经过点(5,
平移后经过点(5,![]() ),则平移后的直线解析式为______________.
),则平移后的直线解析式为______________.
13.计算:(2![]() ﹣1)(1+2
﹣1)(1+2![]() )=_____.
)=_____.
14.已知函数y=2x2-3x+l,当y=1时,x=_____.
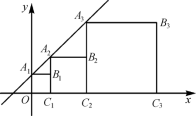
15.将正方形A1B1C1O,A2B2C2C1,A3B3C3C2按如图所示方式放置,点A1,A2,A3,…和点C1,C2,C3,…分别在直线![]() 和x轴上,则点B2019的横坐标是______.
和x轴上,则点B2019的横坐标是______.
16.若最简二次根式![]() 与
与![]() 是同类二次根式,则a=_____.
是同类二次根式,则a=_____.
三、解下列各题(本大题共8小题,共72分)
17.(8分)(1)发现.①![]() ;②
;②![]() ;③
;③![]() ;……写出④ ;⑤ ;
;……写出④ ;⑤ ;
(2)归纳与猜想.如果n为正整数,用含n的式子表示这个运算规律;
(3)证明这个猜想.
18.(8分)先阅读材料:
分解因式:![]() .
.
解:令![]() ,
,
则![]()
![]()
所以![]() .
.
材料中的解题过程用到的是“整体思想”,整体思想是数学解题中常用的一种思想方法,请你运用这种思想方法解答下列问题:
(1)分解因式:![]() __________;
__________;
(2)分解因式:![]() ;
;
(3)证明:若![]() 为正整数,则式子
为正整数,则式子![]() 的值一定是某个整数的平方.
的值一定是某个整数的平方.
19.(8分)随着车辆的增加,交通违规的现象越来越严重,交警对某雷达测速区检测到的一组汽车的时速数据进行整理,得到其频数及频率如表(未完成):
数据段 | 频数 | 频率 |
30~40 | 10 | 0.05 |
40~50 | 36 |
|
50~60 |
| 0.39 |
60~70 |
|
|
70~80 | 20 | 0.10 |
总计 | 200 | 1 |
注:30~40为时速大于等于30千米而小于40千米,其他类同
(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;
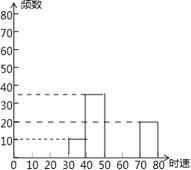
(3)如果汽车时速不低于60千米即为违章,则违章车辆共有多少辆?
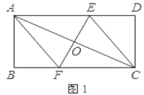
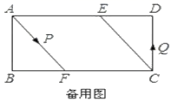
20.(8分)已知,矩形![]() 中,
中,![]() ,
,![]() 的垂直平分
的垂直平分![]() 线分别交
线分别交![]() 于点
于点![]() ,垂足为
,垂足为![]() .
.
(1)如图1,连接![]() ,求证:四边形
,求证:四边形![]() 为菱形;
为菱形;
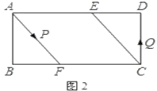
(2)如图2,动点![]() 分别从
分别从![]() 两点同时出发,沿
两点同时出发,沿![]() 和
和![]() 各边匀速运动一周,即点
各边匀速运动一周,即点![]() 自
自![]() 停止,点
停止,点![]() 自
自![]() 停止.在运动过程中,
停止.在运动过程中,
①已知点![]() 的速度为每秒
的速度为每秒![]() ,点
,点![]() 的速度为每秒
的速度为每秒![]() ,运动时间为
,运动时间为![]() 秒,当
秒,当![]() 四点为顶点的四边形是平行四边形时,则
四点为顶点的四边形是平行四边形时,则![]() ____________.
____________.
②若点![]() 的运动路程分别为
的运动路程分别为![]() (单位:
(单位:![]() ),已知
),已知![]() 四点为顶点的四边形是平行四边形,则
四点为顶点的四边形是平行四边形,则![]() 与
与![]() 满足的数量关系式为____________.
满足的数量关系式为____________.
21.(8分)春节前夕,某商店根据市场调查,用2000元购进第一批盒装花,上市后很快售完,接着又用4200元购进第二批这种盒装花.已知第二批所购的盒数是第一批所购花盒数的3倍,且每盒花的进价比第一批的进价少6元.求第一批盒装花每盒的进价.
22.(10分)如图1所示,在![]() 中,
中,![]() 为边
为边![]() 上一点,将
上一点,将![]() 沿
沿![]() 折叠至
折叠至![]() 处,
处,![]() 与
与![]() 交于点
交于点![]() .若
.若![]() ,
,![]() ,则
,则![]() 的大小为_______.
的大小为_______.
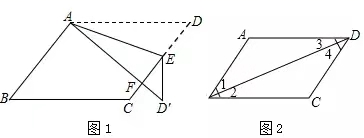
提出命题:如图2,在四边形![]() 中,
中,![]() ,
,![]() ,求证:四边形
,求证:四边形![]() 是平行四边形.
是平行四边形.
小明提供了如下解答过程:
证明:连接![]() .
.
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,![]() .
.
∴![]() ,
,![]() .
.
∴四边形![]() 是平行四边形(两组对边分别平行的四边形是平行四边形).
是平行四边形(两组对边分别平行的四边形是平行四边形).
反思交流:(1)请问小明的解法正确吗?如果有错,说明错在何处,并给出正确的证明过程.
(2)用语言叙述上述命题:______________________________________________.
运用探究:(3)下列条件中,能确定四边形![]() 是平行四边形的是( )
是平行四边形的是( )
A.![]()
B.![]()
C.![]()
D.![]()
23.(10分)学校准备假期组织学生去北京研学,现有甲、乙两家旅行社表示对学生研学团队优惠.设参加研学的学生有x人,甲、乙两家旅行社实际收费分别为![]() 元,
元,![]() 元,且它们的函数图象如图所示,根据图象信息,请你回答下列问题:
元,且它们的函数图象如图所示,根据图象信息,请你回答下列问题:
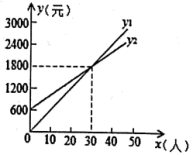
(1)根据图象直接写出当参加研学的学生人数为多少时,两家旅行社收费相同?
(2)当参加老师的人数为多少人时,选择甲旅行社合算?
(3)如果共有50人参加时,通过计算说明选择哪家旅行社合算?
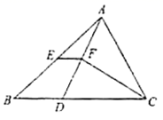
24.(12分)如图所示,在![]() 中,点
中,点![]() 在
在![]() 上,
上,![]() 于
于![]() ,且
,且![]() 平分
平分![]() ,
,![]() .
.
求证:![]() .
.
参考答案
一、选择题(每小题3分,共30分)
1、C
2、A
3、A
4、D
5、A
6、B
7、C
8、D
9、C
10、C
二、填空题(本大题共有6小题,每小题3分,共18分)
11、1
12、y=2x-1
13、7
14、0或![]()
15、![]() .
.
16、1
三、解下列各题(本大题共8小题,共72分)
17、(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
18、(1)![]() ;(2)
;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
19、(1)见解析;(2)见解析;(3)76(辆).
20、(1)见解析;(2)①![]() ;②
;②![]()
21、20元
22、(1)详见解析;(2)两组对角分别相等的四边形是平行四边形;(3)B
23、(1)30人;(2)当有30人以下时,y![]() <y
<y![]() ,所以选择甲旅行社合算;;(3)当
,所以选择甲旅行社合算;;(3)当![]() 人时,乙旅行社合算.
人时,乙旅行社合算.
24、详见解析
广东省深圳市北大附中深圳南山分校2023-2024学年九年级数学第一学期期末教学质量检测模拟试题含答案: 这是一份广东省深圳市北大附中深圳南山分校2023-2024学年九年级数学第一学期期末教学质量检测模拟试题含答案,共9页。试卷主要包含了答题时请按要求用笔,计算的值为,在比例尺为1等内容,欢迎下载使用。
广东省深圳市北大附中深圳南山分校2023-2024学年数学八年级第一学期期末考试模拟试题含答案: 这是一份广东省深圳市北大附中深圳南山分校2023-2024学年数学八年级第一学期期末考试模拟试题含答案,共7页。试卷主要包含了角平分线的作法,为推进垃圾分类,推动绿色发展等内容,欢迎下载使用。
广东省深圳市北大附中南山分校2022-2023学年八年级上学期月考数学试题: 这是一份广东省深圳市北大附中南山分校2022-2023学年八年级上学期月考数学试题,共13页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












