


2022-2023学年深圳市重点中学七下数学期末质量检测模拟试题含答案
展开2022-2023学年深圳市重点中学七下数学期末质量检测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考试结束后,请将本试卷和答题卡一并交回.
2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.
4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.
5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗.
一、选择题(每小题3分,共30分)
1.为了比较某校同学汉字听写谁更优秀,语文老师随机抽取了8次听写情况,发现甲乙两人平均成绩一样,甲、乙的方差分别为1.9和2.3,则下列说法正确的是( )
A.甲的发挥更稳定 B.乙的发挥更稳定
C.甲、乙同学一样稳定 D.无法确定甲、乙谁更稳定
2.若正比例函数![]() 的图像经过第一、三象限,则
的图像经过第一、三象限,则![]() 的值可以是( )
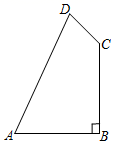
的值可以是( )
A.3 B.0或1 C.![]() D.
D.![]()
3.如图,直线y1=kx和直线y2=ax+b相交于点(1,2).则不等式组ax+b>kx>0的解集为( )
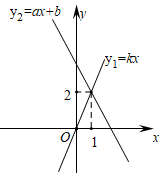
A.x<0 B.0<x<1 C.x<1 D.x<0或x>1
4.下列二次根式计算正确的是( )
A.![]() -
-![]() =1 B.
=1 B.![]() +
+![]() =
=![]() C.
C.![]() ×
×![]() =
=![]() D.
D.![]() ÷
÷![]() =
=![]()
5.下列四个图形中,既是轴对称又是中心对称的图形是( ) 
A.4个 B.3个 C.2个 D.1个
6.中国药学家屠呦呦获2015年诺贝尔医学奖,她的突出贡献是创制新型抗疟药青蒿素和双氢青蒿素,这是中国医学界迄今为止获得的最高奖项,已知显微镜下某种疟原虫平均长度为0.0000015米,该长度用科学记数法可表示为( )
A.![]() 米 B.
米 B.![]() 米 C.
米 C.![]() 米 D.
米 D.![]() 米
米
7.若直线y=kx+b经过一、二、四象限,则直线y=bx﹣k的图象只能是图中的( )
A.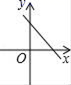 B.
B.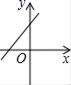 C.
C.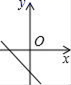 D.
D.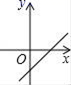
8.若分式![]() 有意义,则a的取值范围为( )
有意义,则a的取值范围为( )
A.a≠4 B.a>4 C.a<4 D.a=4
9.一次函数y1=kx+b与y2=x+a的图象如图,则下列结论①k<0;②a>0;③当x<3时,y1<y2中,正确的个数是( )
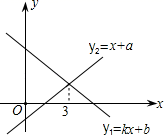
A.0 B.1 C.2 D.3
10.下列各方程中,是一元二次方程的是()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(本大题共有6小题,每小题3分,共18分)
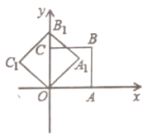
11.如图,在平面直角坐标系中,将正方形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后得到正方形
后得到正方形![]() ,依此方式,绕点
,依此方式,绕点![]() 连续旋转2019次得到正方形
连续旋转2019次得到正方形![]() ,如果点
,如果点![]() 的坐标为(1,0),那么点
的坐标为(1,0),那么点![]() 的坐标为________.
的坐标为________.
12.下表记录了某校4名同学游泳选拨赛成绩的平均数与方差:
| 队员1 | 队员2 | 队员3 | 队员4 |
平均数 | 51 | 50 | 51 | 50 |
方差 | 3.5 | 3.5 | 14.5 | 15.5 |
根据表中数据要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择__________.
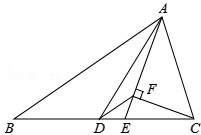
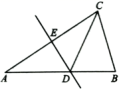
13.如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=2,则DF的长为_________.
14.函数![]() 的自变量x的取值范围______.
的自变量x的取值范围______.
15.小明利用公式![]() 计算5个数据的方差,则这5个数据的标准差
计算5个数据的方差,则这5个数据的标准差![]() 的值是_____.
的值是_____.
16.如图,在四边形ABCD中,AB=BC=2,CD=1,AD=3,若∠B=90°,则∠BCD的度数为____________________.
三、解下列各题(本大题共8小题,共72分)
17.(8分)函数 y=(m-2)x+m2-4 (m为常数).
(1)当m取何值时, y是x的正比例函数?
(2) 当m取何值时, y是x的一次函数?
18.(8分)(1)计算:![]() ;
;
(2)已知![]() ,求代数式
,求代数式![]() 的值.
的值.
19.(8分)如图,在正方形ABCD中,E是CD边的中点,AC与BE相交于点F,连接DF.
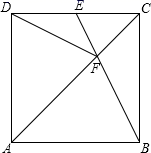
(1)在不增加点和线的前提下,直接写出图中所有的全等三角形;
(2)连接AE,试判断AE与DF的位置关系,并证明你的结论;
(3)延长DF交BC于点M,试判断BM与MC的数量关系.(直接写出结论)
20.(8分)因式分解
(1)![]()
(2)![]()
(3)![]()
(4)![]()
21.(8分)如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的垂直平分线.求证:
的垂直平分线.求证:![]() 是等腰三角形.
是等腰三角形.
22.(10分)A、B 两乡分别由大米 200 吨、300 吨.现将这些大米运至 C、D 两个粮站储存.已知 C 粮站可 储存 240 吨,D 粮站可储存 200 吨,从 A 乡运往 C、D 两处的费用分别为每吨 20 元和 25 元,B 乡 运往 C、D 两处的费用分别为每吨 15 元和 18 元.设 A 乡运往 C 粮站大米 x 吨.A、B 两乡运往两 个粮站的运费分别为 yA、yB 元.
(1)请填写下表,并求出 yA、yB 与 x 的关系式:
| C 站 | D 站 | 总计 |
A 乡 | x 吨 |
| 200 吨 |
B 乡 |
|
| 300 吨 |
总计 | 240 吨 | 260 吨 | 500 吨 |
(2)试讨论 A、B 乡中,哪一个的运费较少;
(3)若 B 乡比较困难,最多只能承受 4830 元费用,这种情况下,运输方案如何确定才能使总运费 最少?最少的费用是多少?
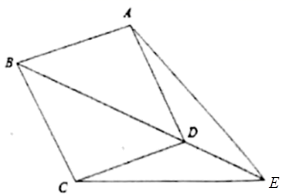
23.(10分)如图,菱形![]() 中,
中,![]() 为对角线
为对角线![]() 的延长线上一点.
的延长线上一点.
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
24.(12分)已知二次函数![]()
(1)若该函数与![]() 轴的一个交点为
轴的一个交点为![]() ,求
,求![]() 的值及该函数与
的值及该函数与![]() 轴的另一交点坐标;
轴的另一交点坐标;
(2)不论![]() 取何实数,该函数总经过一个定点,
取何实数,该函数总经过一个定点,
①求出这个定点坐标;
②证明这个定点就是所有抛物线顶点中纵坐标最大的点。
参考答案
一、选择题(每小题3分,共30分)
1、A
2、A
3、B
4、C
5、C
6、A
7、B
8、A
9、B
10、A
二、填空题(本大题共有6小题,每小题3分,共18分)
11、![]()
12、队员1
13、![]()
14、x<-2
15、![]()
16、135°
三、解下列各题(本大题共8小题,共72分)
17、(1)m=-2;(2) m ≠2时,y是x的一次函数
18、(1)![]() ;(2)0.
;(2)0.
19、(1)△ADF≌△ABF,△ADC≌△ABC,△CDF≌△CBF;(1)AE⊥DF,详见解析;(3)详见解析
20、(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]()
21、见解析
22、(1)表见解析;yA=20x+25×(200−x)=−5x+5000(0⩽x⩽200);yB=15×(240−x)+18×(x+60)=3x+4680(0⩽x⩽200);(2)当x<40时,B乡运费少;当x=40时,A. B两乡运费一样多;当x>40时,A乡运费少;(3)当x=50时,总运费最低,最低费用为9580元.
23、(1)见解析;(2)![]()
24、(1)![]() ;(2)①(2,6);②点(2,6)
;(2)①(2,6);②点(2,6)
长治市重点中学2022-2023学年七下数学期末质量检测模拟试题含答案: 这是一份长治市重点中学2022-2023学年七下数学期末质量检测模拟试题含答案,共6页。试卷主要包含了下列各式运算结果为x8的是,如图,在中,于点若则等于,下列代数式属于分式的是等内容,欢迎下载使用。
榆林市重点中学2022-2023学年数学七下期末质量检测模拟试题含答案: 这是一份榆林市重点中学2022-2023学年数学七下期末质量检测模拟试题含答案,共7页。试卷主要包含了如图,点A等内容,欢迎下载使用。
拉萨市重点中学2022-2023学年七下数学期末质量检测模拟试题含答案: 这是一份拉萨市重点中学2022-2023学年七下数学期末质量检测模拟试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁,下列因式分解正确的是等内容,欢迎下载使用。












