2022-2023学年辽宁省锦州市太和区七年级（下）期中数学试卷（含解析）

这是一份2022-2023学年辽宁省锦州市太和区七年级（下）期中数学试卷（含解析），共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2022-2023学年辽宁省锦州市太和区七年级（下）期中数学试卷
一、选择题（本大题共10小题，共20.0分。在每小题列出的选项中，选出符合题目的一项）
1. 计算a2·a3，结果正确的是(    )
A. a5 B. a6 C. a8 D. a9
2. 计算(−2x4)3=(    )
A. −8x7 B. 8x12 C. −2x12 D. −8x12
3. 计算：4−2=(    )
A. −16 B. 116 C. −116 D. 16
4. 下列能用平方差公式计算的是(    )
A. (a+b)(2a−b) B. (−a−b)(a+b)
C. (−a+b)(a−b) D. (−a+b)(−a−b)
5. 长方形的面积是9a2−6ab，一边长是3a，则它的另一边长是(    )
A. 3a+2b B. 3a−2b C. 2a−3b D. 2a+3b
6. 下列说法错误的是(    )
A. 在同一平面内，不相交的直线互相平行
B. 在同一平面内，没有公共点的线段平行
C. 平行于同一条直线的两条直线平行
D. 经过直线外一点，有且只有一条直线与这条直线平行
7. 如图，直线AB经过点O，若OC⊥OD，则图中∠1与∠2的关系是(    )

A. 对顶角 B. 互为余角 C. 互为邻补角 D. 互为补角
8. 如图，直线a/​/b，∠1=120°，则∠2的度数为(    )
A. 60°
B. 50°
C. 40°
D. 30°
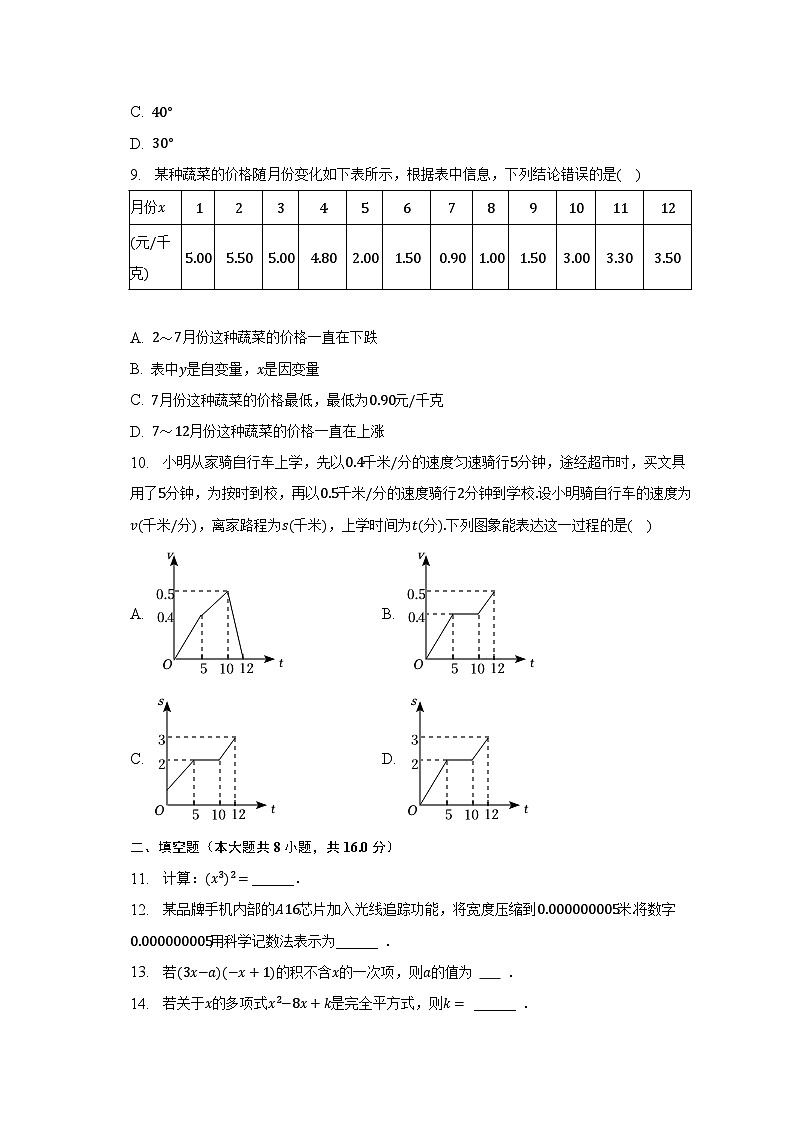
9. 某种蔬菜的价格随月份变化如下表所示，根据表中信息，下列结论错误的是(    )
月份x
1
2
3
4
5
6
7
8
9
10
11
12
(元/千克)
5.00
5.50
5.00
4.80
2.00
1.50
0.90
1.00
1.50
3.00
3.30
3.50

A. 2～7月份这种蔬菜的价格一直在下跌
B. 表中y是自变量，x是因变量
C. 7月份这种蔬菜的价格最低，最低为0.90元/千克
D. 7～12月份这种蔬菜的价格一直在上涨
10. 小明从家骑自行车上学，先以0.4千米/分的速度匀速骑行5分钟，途经超市时，买文具用了5分钟，为按时到校，再以0.5千米/分的速度骑行2分钟到学校.设小明骑自行车的速度为v(千米/分)，离家路程为s(千米)，上学时间为t(分).下列图象能表达这一过程的是(    )
A. B.
C. D.
二、填空题（本大题共8小题，共16.0分）
11. 计算：(x3)2=______．
12. 某品牌手机内部的A16芯片加入光线追踪功能，将宽度压缩到0.000000005米.将数字0.000000005用科学记数法表示为______ ．
13. 若(3x−a)(−x+1)的积不含x的一次项，则a的值为        ．
14. 若关于x的多项式x2−8x+k是完全平方式，则k= ______ ．
15. 某水库的水位在某段时间内持续上涨，初始的水位高度为6米，水位以每小时0.3米的速度匀速上升，则水库的水位高度y米与时间x小时的函数关系式为______ ．
16. 如图，直线AB，CD相交于点O，EO⊥AB于点O，若∠EOD=25°，则∠BOC的度数为______ ．

17. 将一副三角尺(厚度不计)如图摆放，使有刻度的两条边互相平行，则图中∠1的大小为______ ．


18. 如图1，在矩形ABCD中，动点P从点B出发，沿BC，CD，DA运动至点A停止．设点P运动的路程为x，△ABP的面积为y，如果y关于x的函数图象如图2所示，则m的值是______．

三、解答题（本大题共8小题，共64.0分。解答应写出文字说明，证明过程或演算步骤）
19. (本小题16.0分)
计算：
(1)(−2a2)3+2a2⋅a4−a8÷a2；
(2)(−2)2+(2023−π)0−2−2；
(3)(2x+1)(x−2)；
(4)(x−2y+1)(x+2y−1)．
20. (本小题6.0分)
先化简再求值：[(3a+b)2+(b+3a)(b−3a)−6b2]÷(2b)，其中a=−13，b=−2．
21. (本小题6.0分)
如图，在长方形CDEF中，点A，B分别在FC，ED的边上，连接AB，请过AC上的点M作BA的平行线交ED于点N.(请用无刻度直尺和圆规作图，不写作法，保留作图痕迹)

22. (本小题6.0分)
完成下面的证明：
如图，在四边形ABCD中，BE平分∠ABC交线段AD于点E，∠1=∠2，∠C=110°，求∠D的度数．
解：∵BE平分∠ABC(已知)，
∴∠2=∠EBC (______ )，
又∵∠1=∠2(______ )，
∴∠1= ______ (等量代换)，
∴AD/​/BC(______ )，
∠C+∠D=180°(______ )，
又∵∠C=110° (已知)，
∴∠D= ______ (______ ).

23. (本小题6.0分)
某电动车厂2014年各月份生产电动车的数量情况如下表：
时间x/月
1
2
3
4
5
6
7
8
9
10
11
12
月产量y/万辆
8
8.5
9
10
11
12
10
9.5
9
10
10
10.5
(1)在这个过程中自变量、因变量各是什么？
(2)哪个月份电动车的产量最高？哪个月份电动车的产量最低？
(3)哪两个月份之间产量相差最大？根据这两个月的产量，你对电动车厂的厂长有什么建议？
24. (本小题8.0分)
如图是小李骑自行车离家的距离s(km)与时间t(h)之间的关系．
(1)在这个变化过程中自变量______，因变量是______；
(2)小李______时到达离家最远的地方？此时离家______km；
(3)分别写出在1 (4)小李______时与家相距20km．

25. (本小题8.0分)
如图，将边长(a+b)的正方形剪出两个边长分别为a，b的正方形(阴影部分).观察图形，解答下列问题：
(1)根据题意，用两种不同的方法表示阴影部分的面积，即用两个不同的代数式表示阴影部分的面积．
方法1：______ ，方法2：______ ；
(2)从中你发现什么结论呢？______ ，
(3)运用你发现的结论，解决下列问题：
①已知x+y=6，12xy=2，求x2+y2的值；
②已知(2023−x)2+(x−2022)2=9，求(2023−x)(x−2022)的值．

26. (本小题8.0分)
如图，图①是一种网红弹弓的实物图，在两头上系上皮筋，拉动皮筋可形成平面示意图如图②和图③，弹弓的两边可看成是平行的，即AB/​/CD，各活动小组探索∠APD与∠A，∠D之间数量关系时，有如下发现：

(1)在图②所示的图形中，若∠A=30°，∠D=35°，则∠APD= ______ ；
(2)在图⑧中，若∠A=150°，∠APD=60°，则∠D= ______ ；
(3)有同学在图②和图③的基础上，画出了图④所示的图形，其中AB/​/CD，请判断∠α，∠β，∠γ之间的关系，并说明理由．
答案和解析

1.【答案】A 
【解析】
【分析】
此题考查同底数幂的乘法，关键是根据同底数的幂的乘法解答，根据同底数幂的乘法法则解答即可．
【解答】
解：a2⋅a3=a5，
故选：A．

  
2.【答案】D 
【解析】解：(−2x4)3
=(−2)3⋅(x4)3
=−8x12，
故选：D．
先根据积的乘方法则进行计算，再根据幂的乘方法则即可求解．
本题主要考查了积的乘方和幂的乘方，掌握相关的法则是解题的关键．

3.【答案】B 
【解析】解：4−2=142=116，
故选：B．
根据a−p=1ap(a≠0)，进行计算即可解答．
本题考查了负整数指数幂，熟练掌握a−p=1ap(a≠0)是解题的关键．

4.【答案】D 
【解析】解：A、(a+b)(2a−b)不能用平方差公式计算，故本选项不符合题意；
B、(−a−b)(a+b)=−(a+b)(a+b)=−(a+b)2，不能用平方差公式计算，故本选项不合题意；
C、(−a+b)(a−b)=−(a−b)×(a−b)=−(a−b)2，不能用平方差公式计算，故本选项不合题意；
D、(−a+b)(−b−a)=−(a−b)×[−(a+b)]=(a−b)(a+b)=a2−b2，能用平方差公式计算，故本选项符合题意；
故选：D．
判断所给式子能否写成两数之和乘以相同两数之差的形式即可．
本题考查平方差公式，能熟记平方差公式(a−b)(a+b)=a2−b2是解题的关键．

5.【答案】B 
【解析】解：∵长方形的面积是9a2−6ab，一边长是3a，
∴它的另一边长是：(9a2−6ab)÷3a=9a2÷3a−6ab÷3a=3a−2b．
故选：B．
直接利用整式的除法运算法则计算得出答案．
此题主要考查了整式的除法运算，正确掌握相关运算法则是解题关键．

6.【答案】B 
【解析】解：A、在同一平面内，不相交的直线互相平行，说法正确，
该选项不符合题意；
B、在同一平面内，没有公共点的线段平行，根据平行线定义，是直线而不是线段，说法错误，
该选项符合题意；
C、平行于同一条直线的两条直线平行，根据平行线的判定与性质，说法正确，
该选项不符合题意；
D、经过直线外一点，有且只有一条直线与这条直线平行，根据平行公理，说法正确，
该选项不符合题意；
故选：B．
根据平行线的定义、相关公理、定理及性质逐项验证即可得到答案．
本题考查平行线的定义、相关公理、定理及性质，熟记有关平行线的定义、相关公理、定理及性质是解决问题的关键．

7.【答案】B 
【解析】解：∵OC⊥OD，
∴∠COD=90°，
∴∠1+∠2=90°，
∴∠1与∠2的关系是互为余角．
故选：B．
根据OC⊥OD得到∠COD=90°，进而得到∠1+∠2=90°，根据互为余角的定义即可得解．
本题考查了互为余角的定义，熟练掌握互为余角的定义是解题的关键．

8.【答案】A 
【解析】解：

∵a/​/b，
∴∠2=∠3，
∵∠1+∠3=180°，
∴∠1+∠2=180°，
∵∠1=120°，
∴∠2=180°−∠1=60°，
故选：A．
根据平行线的性质得出∠2=∠3，再根据∠1+∠3=180°，得出∠1+∠2=180°，即可得出答案．
本题考查平行线的性质，掌握两直线平行，同位角相等是解题的关键．

9.【答案】B 
【解析】解：A：由表格数据可以发现，2～7月份这种蔬菜的价格一直在下跌，A说法正确，故A不符合题意；
B：表中x是自变量，y是因变量，B说法错误，故B符合题意；
C：由表格数据可以发现，7月份这种蔬菜的价格最低，最低为0.90元/千克，C说法正确，故C不符合题意；
D：由表格数据可以发现，7～12月份这种蔬菜的价格一直在上涨，D说法正确，故D不符合题意；
故选：B．
列表法可以具体反映自变量与因变量的对应关系，根据表格中数据判断即可．
本题考查了函数的表示方法，列表法可以具体反映自变量与因变量的对应关系，理解表格中两个变量之间的关系是解本题的关键．

10.【答案】D 
【解析】解：由题意，得：
先以0.4千米/分的速度匀速骑行5分钟，离家路程从0开始随时间匀速增加至2千米；途经超市时，买文具用了5分钟，路程不变；再以0.5千米/分的速度骑行2分钟到学校，离家路程随时间匀速增加至3千米，
故选：D．
根据匀速行驶，可得路程随时间匀速增加，根据途经超市时，买文具用了5分钟，路程不变，根据再以0.5千米/分的速度骑行2分钟到学校，离家路程随时间匀速增加，可得答案．
本题考查了函数图象，根据题意判断路程与时间的关系是解题关键，注意休息时路程不变．

11.【答案】x6 
【解析】解：(x3)2=x6．
故填x6．
根据幂的乘方，底数不变指数相乘计算即可．
本题考查幂的乘方，底数不变指数相乘的性质，熟练掌握运算性质是解题的关键．

12.【答案】5×10−9 
【解析】解：0.000000005=5×10−9．
故答案为：5×10−9．
科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正数；当原数的绝对值<1时，n是负数．
此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数，表示时关键要正确确定a的值以及n的值．

13.【答案】−3 
【解析】解：(3x−a)(−x+1)=−3x2+3x+ax−a=−3x2+(3+a)x−a，
∵积中不含x的一次项，
故3+a=0，
解得a=−3，
故答案为：−3．
根据多项式乘多项式法则计算，然后根据积中不含x的一次项，即可求解．
本题考查多项式乘多项式，熟知多项式乘多项式计算法则是解题的关键．

14.【答案】16 
【解析】解：∵关于x的多项式x2−8x+k是完全平方式，
∴x2−8x+k=x2−2⋅x⋅4+42，
∴k=42=16，
故答案为：16．
根据完全平方公式得出k=42，求出即可．
本题考查了对完全平方式的应用，注意：完全平方式有两个：a2+2ab+b2和a2−2ab+b2．

15.【答案】y=6+0.3x 
【解析】解：因为初始的水位高度为6米，水位以每小时0.3米的速度匀速上升，
所以k=0.3，b=6，
根据题意可得：y=6+0.3x，
故答案为：y=6+0.3x．
根据高度等于速度乘以时间列出关系式解答即可．
此题考查函数关系式，关键是根据题中水位以每小时0.3米的速度匀速上升列出关系式．

16.【答案】65° 
【解析】解：∵OE⊥AB，
∴∠AOE=90°，
即∠AOD+∠DOE=90°，
∵∠EOD=25°，
∴∠AOD=65°，
∴∠BOC=∠AOD=65°，
故答案为：65°．
利用对顶角和互余的角的关系进行计算即可．
本题考查的是余角的定义，对顶角的定义，解题的关键就是要找准对顶角的位置，互余的两个角的和为90度．

17.【答案】105° 
【解析】解：如图：

∵AB//DE，
∴∠BDE=∠B=30°，
又∵∠EDF=45°，
∴∠BDF=75°，
∴∠1=180°−∠BDF=105°．
故答案为：105°．
根据平行线的性质可得∠BDE=∠B=30°，再根据三角尺各角的度数以及邻补角的定义即可得∠1的度数．
此题主要考查了平行线的性质以及邻补角的定义，关键是掌握两直线平行，内错角相等．

18.【答案】5 
【解析】解：由函数图象上的点(2,3)，可知BC=2，
由三角形面积公式，得12×BC×AB=3，解得AB=3，
∴CD=AB=3，m=BC+CD=5．
故答案为：5．
由函数图象可知当x=2时，y=3，可知BC=2，由面积公式可知AB=3，即CD=AB=3，m=BC+CD=5．
本题考查了动点问题的函数图象．关键是根据函数图象发现相关的信息．

19.【答案】解：(1)(−2a2)3+2a2⋅a4−a8÷a2
=−8a6+2a6−a6
=−7a6；
(2)(−2)2+(2023−π)0−2−2
=4+1−14
=5−14
=194；
(3)(2x+1)(x−2)
=2x2−4x+x−2
=2x2−3x−2；
(4)(x−2y+1)(x+2y−1)
=[x−(2y−1)][x+(2y−1)]
=x2−(2y−1)2，
=x2−4y2+4y−1． 
【解析】(1)先算乘方，再算乘除，后算加减，即可解答；
(2)先化简各式，然后再进行计算即可解答；
(3)利用多项式乘多项式的法则，进行计算即可解答
(4)利用平方差公式，完全平方公式，进行计算即可解答．
本题考查了整式的混合运算，平方差公式，完全平方公式，实数的运算，零指数幂，负整数指数，准确熟练地进行计算是解题的关键．

20.【答案】解：[(3a+b)2+(b+3a)(b−3a)−6b2]÷(2b)
=(9a2+6ab+b2+b2−9a2−6b2)÷(2b)
=(6ab−4b2)÷(2b)
=3a−2b，
当a=−13，b=−2时，原式=3×(−13)−2×(−2)=3． 
【解析】根据完全平方公式、平方差公式将括号内的式子展开，然后合并同类项，再除以括号外的式子，然后将a、b的值代入化简后的式子计算即可．
本题考查整式化简求值，解题的关键是熟练掌握整式混合运算法则，准确计算．

21.【答案】解：如图，MN即为所求．
 
【解析】作∠NMC=∠BAC交ED于点N即可．
本题考查了作图−复杂作图，矩形的性质，解决本题的关键是掌握基本作图方法．

22.【答案】角平分线性质  已知  ∠EBC  内错角相等，两直线平行  两直线平行，同旁内角互补  70°  等式的性质 
【解析】解：∵BE平分∠ABC(已知)，
∴∠2=∠EBC (角平分线性质)，
又∵∠1=∠2(已知)，
∴∠1=∠EBC(等量代换)，
∴AD/​/BC(内错角相等，两直线平行)，
∴∠C+∠D=180°(两直线平行，同旁内角互补)，
又∵∠C=110° (已知)，
∴∠D=180°−∠C=70°(等式的性质)，
故答案为：角平分线性质；已知；∠EBC；内错角相等，两直线平行；两直线平行，同旁内角互补；70°；等式的性质．
根据已知条件，利用由角平分线性质，平行线的性质和判定进行解答即可．
本题主要考查了平行线的性质和判定，解题关键是熟练掌握平行线的性质和判定，能够正确识别图形．

23.【答案】解：(1)自变量是时间x，因变量是月产量y．
(2)由表格得，6月份产量最高，1月份产量最低．
(3)1月份与6月份产量相差最大，建议：根据这两个月的电动车的产量要注意1月份劳动力过剩，6月份劳动力不足的问题，注意用工人员的分配． 
【解析】(1)根据自变量与因变量的定义解决此题．
(2)根据表格解决此题．
(3)根据产量情况给出建议．
本题主要考查变量与常量，熟练掌握自变量与因变量的定义是解决本题的关键．

24.【答案】离家时间  离家距离  2  30  20  5 32h或4h 
【解析】解：(1)根据图象可知，在这个变化过程中自变量是离家时间，因变量是离家距离；
(2)根据图象可知小李2h后到达离家最远的地方，此时离家30km；
(3)当1 所以小李在这段时间的速度为：201=20(km/h)，
当2 所以小李在这段时间的速度为：102=5(km/h)；
(4)根据图象可知：小李32h或4h与家相距20km．
故答案为：(1)离家时间；离家距离；(2)2；30；(3)20；5；(4)32h或4h．
(1)在坐标系中横坐标是自变量，纵坐标是因变量，据此求解；
(2)根据图象可以得到离家最远时的时间，此时离家的距离，据此即可确定；
(3)根据图象可以得到从1时开始到2时自行车移动的距离和所用的时间，从2时开始到4时自行车移动的距离和所用的时间，据此即可求得；
(4)根据图象可以得到有两个时间点，据此即可确定．
本题主要考查了函数的图象，需要从图象分析出实际问题，解题的关键是理解横轴和纵轴表示的含义，转化为实际问题中的数据．

25.【答案】a2+b2  (a+b)2−2ab  a2+b2=(a+b)2−2ab 
【解析】解：(1)方法1，阴影部分的面积等于两个正方形的面积和，即a2+b2，
方法2，从边长为(a+b)的大正方形面积减去两个长为a，宽为b的长方形面积，即(a+b)2−2ab，
故答案为：a2+b2，(a+b)2−2ab；
(2)∵(1)中的两种方法都表示阴影部分面积，
∴a2+b2=(a+b)2−2ab，
故答案为：a2+b2=(a+b)2−2ab；
(3)①∵12xy=2，
∴xy=4，
又∵x+y=6，
∴x2+y2=(x+y)2−2xy
=62−2×4
=36−8
=28；
∴x2+y2的值为28；
②设a=2023−x，b=x−2022，则a2+b2=9，a+b=1，
∵a2+b2=(a+b)2−2ab，
∴2ab=(a+b)2−(a2+b2)=12−9=−8，
∴2(2023−x)(x−2022)=−8，
∴(2023−x)(x−2022)=−4，
答：(2023−x)(x−2022)的值为−4．
(1)方法1采用两个正方形的面积和，方法2用大正方形的面积减去两个长方形的面积；
(2)利用面积相等得出结论；
(3)①由(2)的结论，代入计算即可；
②设a=2023−x，b=x−2022，则a2+b2=9，a+b=1，再整体代入计算即可．
本题考查完全平方公式的几何背景，灵活将公式进行变形是解题的关键．

26.【答案】65°  150° 
【解析】解：(1)如图所示，过点P作PQ/​/AB，

∵AB/​/CD，
∴AB//PQ//CD，
∴∠APQ=∠A=30°，∠DPQ=∠D=35°，
∴∠APD=∠APQ+∠DPQ=65°，
故答案为：65°；
(2)如图所示，过点P作PQ/​/AB，

∵AB/​/CD，
∴AB//PQ//CD，
∴∠APQ=180°−∠A=30°，∠D=180°−∠DPQ，
∵∠APD=60°，
∴∠DPQ=∠APD−∠APQ=30°
∴∠D=150°，
故答案为：150°；
(3)∠β=180°−∠α+∠γ，理由如下：
如图所示，过点P作PQ/​/AB，

∵AB/​/CD，
∴AB//PQ//CD，
∴∠BPQ=180°−∠B，∠DPQ=∠D，
∴∠BPD=∠BPQ+∠∠DPQ=180°−∠B+∠D，
∴∠β=180°−∠α+∠γ．
(1)如图所示，过点P作PQ/​/AB，利用平行线的性质得到∠APQ=∠A=30°，∠DPQ=∠D=35°由此即可得到答案；
(2)如图所示，过点P作PQ/​/AB，利用平行线的性质得到∠APQ=180°−∠A=30°，∠D=180°−∠DPQ，在求出∠DPQ的度数即可得到答案；
(3)如图所示，过点P作PQ/​/AB，由平行线的性质得到∠BPQ=180°−∠B，∠DPQ=∠D，再由∠BPD=∠BPQ+∠∠DPQ=180°−∠B+∠D即可得到结论．
本题主要考查了平行线的性质，正确作出辅助线是解题的关键．