高考数学一轮复习考点测试刷题本25 解三角形的应用（含答案解析）

这是一份高考数学一轮复习考点测试刷题本25 解三角形的应用（含答案解析），共8页。
2020高考数学(文数)考点测试刷题本25 解三角形的应用 一         、选择题1.在△ABC中，若A，B，C成等差数列，且AC=，BC=2，则A=(　　)A．135°         B．45°        C．30°          D．45°或135°  2.海上有三个小岛A，B，C，测得∠BAC=135°，AB=6，AC=3，若在B，C两岛的连线段之间建一座灯塔D，使得灯塔D到A，B两岛距离相等，则B，D间的距离为(　　)A．3          B．           C．          D．3  3.一船自西向东匀速航行，上午10时到达一座灯塔P的南偏西75°距塔68海里的M处，下午2时到达这座灯塔的东南方向的N处，则这只船的航行速度为(　　)A．海里/小时    B．34海里/小时    C．海里/小时    D．34海里/小时  4.在△ABC中，内角A，B，C所对的边分别为a，b，c．若==，则△ABC的形状为(　　)A．等边三角形                          B．等腰直角三角形C．有一个角为30°的直角三角形          D．有一个角为30°的等腰三角形  5.如图所示，为了测量某湖泊两侧A，B间的距离，李宁同学首先选定了与A，B不共线的一点C(△ABC的角A，B，C所对的边分别记为a，b，c)，然后给出了三种测量方法：①测量A，C，b；②测量a，b，C；③测量A，B，a，则一定能确定A，B间的距离的所有方案的序号为(　　)A．①②           B．②③           C．①③        D．①②③  6.在△ABC中，B=，BC边上的高等于BC，则cosA=(　　)A．  B．  C．－  D．－  7.若两座灯塔A和B与海洋观察站C的距离都等于a km，灯塔A在观察站C的北偏东20°方向上，灯塔B在观察站C的南偏东40°方向上，则灯塔A与灯塔B的距离为(　　)A．a km         B．a km         C．2a km        D．a km  8.我国南宋著名数学家秦九韶发现了由三角形三边求三角形面积的“三斜公式”，设△ABC的三个内角A，B，C所对的边分别为a，b，c，面积为S，则“三斜求积”公式为S=．若a2sinC=4sinA，(a＋c)2=12＋b2，则用“三斜求积”公式求得△ABC的面积为(　　)A．           B．2           C．3           D． 二         、填空题9.一艘海监船在某海域实施巡航监视，由A岛向正北方向行驶80海里至M处，然后沿东偏南30°方向行驶50海里至N处，再沿南偏东30°方向行驶30海里至B岛，则A，B两岛之间的距离是________海里．  10.某中学举行升旗仪式，在坡度为15°的看台E点和看台的坡脚A点，分别测得旗杆顶部的仰角分别为30°和60°，量得看台坡脚A点到E点在水平线上的射影B点的距离为10 m，则旗杆的高是________m．  11.已知△ABC，AB=AC=4，BC=2．点D为AB延长线上一点，BD=2，连接CD，则△BDC的面积是________，cos∠BDC=________．  12.如图所示，当甲船位于A处时获悉，在其正东方向相距20海里的B处有一艘渔船遇险等待营救，甲船立即前往营救，同时把消息告知在甲船的南偏西30°相距10海里C处的乙船，乙船立即朝北偏东θ＋30°角的方向沿直线前往B处营救，则sinθ的值为________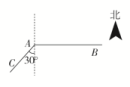． 三         、解答题13.如图，在△ABC中，已知点D在BC边上，满足AD⊥AC，cos∠BAC=－，AB=3，BD=．(1)求AD的长；(2)求△ABC的面积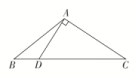．           14.在△ABC中，a，b，c分别为内角A，B，C的对边，且满足cos(A－B)=2sinAsinB．(1)判断△ABC的形状；(2)若a=3，c=6，CD为角C的平分线，求CD的长．                   15.在△ABC中，内角A，B，C所对的边分别为a，b，c．已知b＋c=2acosB．(1)证明：A=2B；(2)若△ABC的面积S=，求角A的大小．                           16.在△ABC中，内角A，B，C的对边分别为a，b，c.若C=，且sin(A＋C)=2sin Acos(A＋B)．(1)求证：a，b,2a成等比数列；(2)若△ABC的面积是1，求c的长．                  
答案解析1.答案为：B；解析：因为A，B，C成等差数列，所以B=60°．由正弦定理，得=，则sinA=．又BC＜AC，所以A＜B，故A=45°．故选B．  2.答案为：B；解析：由题意可知，D为线段AB的垂直平分线与BC的交点，设BD=t．由余弦定理可得BC2=62＋(3)2－2×6×3cos∠BAC=90，解得BC=3．由cos∠ABC==，解得t=．故选B．  3.答案为：A；解析：如图所示，在△PMN中，=，∴MN==34．∴v==(海里/小时)．故选A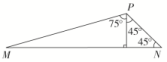．  4.答案为：B；解析：由正弦定理，得==，又==，两式相除，得1=tanB=tanC，所以B=C=45°．所以A=90°，故△ABC为等腰直角三角形．故选B．  5.答案为：D；解析：由题意可知，在①②③三个条件下三角形均可唯一确定，通过解三角形的知识可求出AB．故选D．  6.答案为：C；解析：过A作AD⊥BC，垂足为D，由题意知AD=BD=BC，则CD=BC，AB=BC，AC=BC，在△ABC中，由余弦定理的推论可知，cos∠BAC===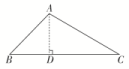－．  7.答案为：D；解析：如图所示，依题意知∠ACB=180°－20°－40°=120°，AC=BC=a km，在△ABC中，由余弦定理知AB==a(km)，即灯塔A与灯塔B的距离为a km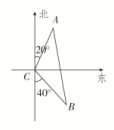．  8.答案为：A；解析：由正弦定理得a2c=4a，所以ac=4，且a2＋c2－b2=12－2ac=4，代入面积公式得=．故选A．   一         、填空题9.答案为：70；解析：依题意画出图形，连接AN，则在△AMN中，应用余弦定理可得AN2=502＋802－2×50×80×cos60°，即AN=70．应用余弦定理可得cos∠ANM==，所以sin∠ANM=．在△ANB中，应用余弦定理可得AB2=(30)2＋702－2×30×70×cos∠ANB，而cos∠ANB=cos(150°－∠ANM)=cos150°cos∠ANM＋sin150°·sin∠ANM=，所以AB==70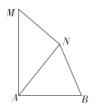．  10.答案为：10(3－)；解析：由题意得∠DEA=45°，∠ADE=30°，AE=，所以AD==，因此CD=ADsin60°=×sin60°=10(3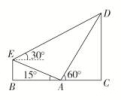－)．  11.答案为：，；解析：∵AB=AC=4，BC=2，∴cos∠ABC==．∵∠ABC为三角形的内角，∴sin∠ABC=，∴sin∠CBD=，故S△CBD=×2×2×=．∵BD=BC=2，∴∠ABC=2∠BDC．又cos∠ABC=，∴2cos2∠BDC－1=，得cos2∠BDC=，又∠BDC为锐角，∴cos∠BDC=． 12.答案为：；解析：如图，连接BC，在△ABC中，AC=10，AB=20，∠BAC=120°，由余弦定理，得BC2=AC2＋AB2－2AB·AC·cos120°=700，∴BC=10，再由正弦定理，得=，∴sinθ=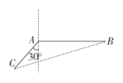．   二         、解答题13.解：(1)因为AD⊥AC，cos∠BAC=－，且∠BAC∈(0，π)，所以sin∠BAC=．又sin∠BAC=sin＋∠BAD=cos∠BAD=，在△ABD中，BD2=AB2＋AD2－2AB·ADcos∠BAD，即AD2－8AD＋15=0，解得AD=5或AD=3，由于AB>AD，所以AD=3．(2)在△ABD中，=，又由cos∠BAD=，得sin∠BAD=，所以sin∠ADB=，则sin∠ADC=sin(π－∠ADB)=sin∠ADB=．因为∠ADB=∠DAC＋∠C=＋∠C，所以cosC=．在Rt△ADC中，cosC=，则tanC===，所以AC=3．则△ABC的面积S=AB·AC·sin∠BAC=×3×3×=6．  14.解：(1)由cos(A－B)=2sinAsinB，得cosAcosB＋sinAsinB=2sinAsinB，∴cosAcosB－sinAsinB=0，∴cos(A＋B)=0，∴C=90°．故△ABC为直角三角形．(2)由(1)知C=90°，又a=3，c=6，∴b==3，A=30°，∠ADC=180°－30°－45°=105°．由正弦定理得=，∴CD=×sin30°=×=．  15.解：(1)证明：由正弦定理得sinB＋sinC=2sinAcosB，故2sinAcosB=sinB＋sin(A＋B)=sinB＋sinAcosB＋cosAsinB，于是sinB=sin(A－B)．又A，B∈(0，π)，故0<A－B<π，所以，B=π－(A－B)或B=A－B，因此A=π(舍去)或A=2B，所以A=2B．(2)由S=得absinC=，故有sinBsinC=sin2B=sinBcosB，因sinB≠0，得sinC=cosB．又B，C∈(0，π)，所以C=±B．当B＋C=时，A=；当C－B=时，A=．综上，A=或A=．  16.解：(1)证明：∵A＋B＋C=π，sin(A＋C)=2sin Acos(A＋B)，∴sin B=－2sin Acos C.在△ABC中，由正弦定理得，b=－2acos C，∵C=，∴b=a，则b2=a·2a，∴a，b,2a成等比数列．(2)S△ABC=absin C=ab=1，则ab=2，由(1)知，b=a，联立两式解得a=，b=2，由余弦定理得c2=a2＋b2－2abcos C=2＋4－4×=10，∴c=.